서 론
하천수를 수원으로 하는 취수방법으로는 취수보, 취수탑, 취수문, 취수관거 방식이 있다. 이러한 취수 방식 중 가장 일반 적인 방식은 콘크리트 취수보이다. 그러나 콘크리트 취수보는 불투수성 횡단구조물로서, 유기오염물질의 정체로 인한 부영양화로 수질오염을 악화시키고, 상하류 어종의 이동이 제한되어 수 생태계의 단절을 야기하는 문제점이 있으며, 토사퇴적으로 인한 건천화를 유발하여 취수보로서의 원래 기능을 상실할 수 있다. 콘크리트 대신 자연석이나 쇄석을 채움재로 하는 돌망태를 취수보로 사용한다면 수위를 상승시켜 취수보의 기능을 구현할 수 있을 뿐 아니라 하천수 중의 부유물질들의 이동을 허용하여 수질악화와 토사퇴적을 방지할 수 있다. 더욱이 댐체 내부에 여과재와 유공관을 구비하면 간접취수에 의한 수질정화 효과 또한 기대할 수 있을 것이다. 콘크리트 취수보의 방류량은 보의 제원과 월류수심에 좌우되나, 돌망태 취수보의 경우에는 채움재의 형상, 입경, 간극비에 관한 정보가 추가로 필요하다. 이처럼 방류량 산출식에서 돌망태 채움재의 물리적 특성인자를 도출하여, 다른 인자들과의 상관관계를 필요로 하는 것이 콘크리트 취수보와 다른 점이다. Hussein et al.(1997)은 사력댐의 흐름해석을 위하여, 마찰계수와 레이놀즈 수의 관계로 부터 1차원 비선형 수두손실방정식을 제시하였으며, 채움재의 입경, 형상, 배치상태를 수리특성화하는 방법을 제시하였다. Hussein et al.(1998)은 연속하여 모형실험을 통하여 돌망태 보의 길이, 채움재와 물의 실험상수, 상류수심을 알면 방류량을 구할 수 있는 방정식을 제시하였다. Mohamed(2010)는 차원해석으로부터 변수들을 무차원화하고, 모형실험을 통하여 무차원변수들 간의 관계식을 도출하고, 돌망태 보의 유량계수 산정식을 개발하여, 기존 콘크리트 보의 방류량 산출식에 적용 가능하다고 하였다. Siddiqua et al.(2011)은 150 mm 크기 입경의 채움재까지 실험할 수 있는 장치를 만들고, 다양한 크기와 분급의 채움재에 의한 난류의 거동을 관찰하였다. Mohamed and Mohamed(2015)은 돌망태 보에서의 흐름을 통과류(Through flow)와 천이류(Transition flow)로 구분하고, 차원해석과 다중회귀분석을 통하여 상류수심을 구하는 방정식을 제시하였다. Leandro and Eusebio(2017)은 모형실험을 통하여, 채움재의 크기, 형상 그리고 수로경사가 돌망태 보의 흐름특성에 미치는 영향을 관찰하고 돌망태 보 채움재의 물리적 특성은 하천의 수리수문학적 특성을 결정짓는다고 하였다. Hazart et al.(2019)은 모형실험을 통하여 콘크리트 보와 돌망태 보의 유량계수, 기초누수, 토사퇴적, 수심의 차이를 관찰하고, 수치해석으로 분석하였다.
본 연구는 하천수를 이용한 인공함양 원수를 확보하는데 있어서, 돌망태 보의 저류와 취수성능을 검토하기 위하여 수행되었다. 기존의 방류량 산출식을 고찰하여 돌망태 취수보의 수심-유량관계를 잘 표현할 수 있는 식을 선정하고, Test bed 수계에 적용하였다. 저류성능은 채움재 입경별 상류수심을 계산하여 평가하였으며, 취수성능은 산출된 상류수심을 입력변수로 사용하여 간접취수량을 계산하여, 취수율로 평가하였다.
수심-유량 관계식 도출
콘크리트 취수보
콘크리트 취수보는 일반적으로 사각위어(Rectangular weir) 형식(Fig. 1a)과 월류댐(Overflow spillway) 형식(Fig. 1b)이 사용되고 있다. 콘크리트 취수보의 방류량은 보 정점의 형상, 폭, 높이, 그리고 월류수심에 따라 다르다. 사각위어의 경우, 층을 통과하는 유량은 식 (1)과 같고, 보 전체단면의 유량은 식 (2)와 같이 표현할 수 있다. 실제 유량은 정점부근의 근접유속과 수두손실 때문에 식 (3)과 같이 표현되고, 월류댐의 경우는 식 (4)와 같다.
| $$dQ=bdz\;v=b\sqrt{2gz}dz$$ | (1) |
| $$Q=b\sqrt{2g}\int_0^H\sqrt zdz$$ | (2) |
| $$Q= \frac {2}{3} C _{d} b \sqrt {2g} h _{o}^{3/2} =Cbh _{o}^{3/2}$$ | (3) |
| $$Q=CLh_o^{3/2}$$ | (4) |
여기서, 는 실험상수 를 포함한 의 값을 가지는 유량계수이며, 월류수심 , 보의 높이 , 보의 길이 , 수로의 폭 , 보의 폭 에 따라 실험에 의해서 결정된다. 월류댐의 유량계수 는 2.21을 적용하며. 사각위어의 실험상수 는 월류수맥의 수축을 무시할 경우, 식 (5)와 같다(Lee et al., 2002).
| $$C _{d} =0.605+ \frac{1} {1000h _{o}} +0.08 \frac{h _{o}} {H _{}}$$ | (5) |
식 (3)과 식 (4)에서 보의 높이와 길이가 각각 1.0 m, 1.0 m일 때, 유량을 독립변수로 하여 수심을 구하는 수심-유량관계식은 식 (6), (7)과 같다.
| $$h_o=0.589\times q^{0.666},\;(H=1.0\;m,\;L=1.0\;m,\;C=2.08\sim2.02)$$ | (6) |
| $$h_o=0.660\times q^{0.668},\;(H=1.0\;m,\;L=1.0\;m,\;C=2.21)$$ | (7) |
돌망태 취수보
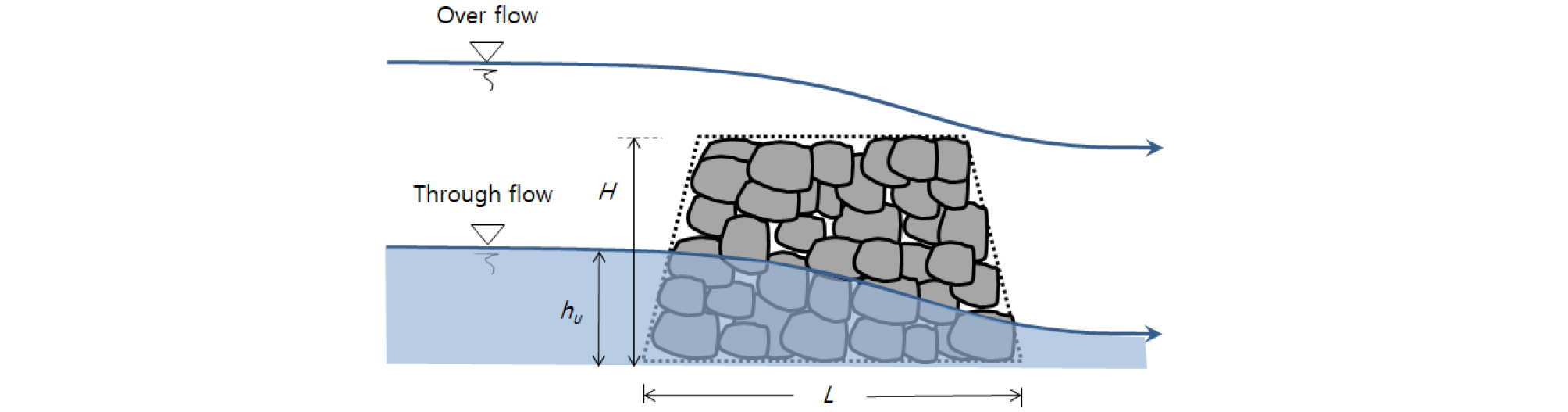
돌망태 취수보의 흐름영역은 콘크리트 취수보의 월류외에 통과류가 있으며, 보의 높이, 보의 길이, 보의 상류수심 외에 채움재의 형상, 입경, 배치상태 등이 흐름에 영향을 미친다(Fig. 2).
Mohamed(2010)는 돌망태 보의 월류에 영향을 미치는 인자들을 식 (8)과 같이 정의하고, 영향인자들 간의 무차원관계식을 식 (9)와 같이 유도하였으며, 유량계수 산정식을 식 (10)과 같이 도출하였다.
| $$q=f(h_u,\;h_d,\;b,\;H,\;h_o,\;l,\;d_m,\;\rho,\;g,\;\mu)$$ | (8) |
| $$\frac Q{\sqrt gBh_u^{1.5}}=\phi\left(\frac{Q\rho}{b\mu},\;\frac{h_o}L,\;\frac{d_m}H,\;\frac{h_u-h_d}{h_o}\right)$$ | (9) |
| $$C=-1.31+0.47logR _{e} -0.84h _{o} /L+1.01d _{m} /H$$ | (10) |
여기서, 는 보의 하류수심, 는 물의 밀도, 는 중력가속도, 는 물의 동점성계수이다. 는 Froude 수, 는 Reynolds 수, 는 마찰경사이다. 식 (9)를 식 (3)에 적용하면 방류량을 구할 수 있으며, 수심-유량관계식으로 전환하면 식 (11)~(13)과 같다.
| $$h_o=0.5661\times q^{0.6667},\;(H=1.0\;m,\;L=1.0\;m,\;d_m=29.0\;mm,\;C=3.61\sim3.65)$$ | (11) |
| $$h_o=0.6228\times q^{0.6667},\;(H=1.0\;m,\;L=1.0\;m,\;d_m=7.0\;mm,\;C=3.01\sim2.23)$$ | (12) |
| $$h_o=0.7428\times q^{0.6667},\;(H=1.0\;m,\;L=1.0\;m,\;d_m=2.8\;mm,\;C=2.42\sim2.51)$$ | (13) |
Hussein et al.(1998)은 채움재의 공극을 통한 방류량과 보의 상류수심의 관계를 식 (14)와 같이 제시하였다.
| $$q _{v} =\left( \frac{i _{eq}} {a _{v}} \right) ^{\frac{1}{b ^{v}}} \times h _{u}$$ | (14) |
여기서, 는 공극유량이며, 돌망태 보의 단위폭 당 방류량 를 채움재의 공극율 으로 나눈 값이다. 는 채움재 수리경사의 대표값을 의미하는 등가수리경사이며, 의 범위에서 의 관계가 있다. 는 유체와 매질의 특성을 표현하며, 는 난류정도를 나타내는 실험상수이고, 1.0~2.0의 값을 갖는다. 는 보의 상류수심이다. 한편, 돌망태 채움재의 형상, 입경과 거칠기가 흐름에 미치는 영향을 표현하기 위하여 동수평균반경(Garga et al., 1990)을 구하는 식 (15)를 도입하였다.
| $$m= \frac {ed _{m}} {6r _{e}}$$ | (15) |
여기서, 은 동수평균반경, 는 공극비, 은 채움재의 평균입경, 는 채움재의 형상계수이며, 완전한 구(Sphere)의 비표면적과의 비를 의미한다. 식 (14)를 수심-유량관계식으로 전환하면 식 (16)~(18)과 같다.
| $$h_u=0.271\times q^{0.629},\;(L=1.0\;m,\;d_m=22.5\;mm,\;m=0.14,\;a_v=0.004,\;b_v=1.697)$$ | (16) |
| $$h_u=0.376\times q^{0.613},\;(L=1.0\;m,\;d_m=12.5\;mm,\;m=0.07,\;a_v=0.011,\;b_v=1.585)$$ | (17) |
| $$h_u=0.992\times q^{0.605},\;(L=1.0\;m,\;d_m=3.75\;mm,\;m=0.02,\;a_v=0.047,\;b_v=1.531)$$ | (18) |
Mohamed and Mohamed(2015)은 돌망태 보의 통과류에 영향을 미치는 인자들을 식 (19)와 같이 정의하고, 차원해석을 수행하여 영향인자들 간의 무차원관계식을 식 (20)과 같이 유도하였으며, 변수량들의 다중회귀분석을 통하여 상류수심을 구하는 관계식을 식 (21)과 같이 도출하였다.
| $$h_u=f(\rho,\;g,\;q,\;L,\;d_m)$$ | (19) |
| $$\frac{q} {g ^{0.5} h _{u}^{1.5} } = \phi\left( \frac{L} {h _{u}} , \frac{d _{m}} {h _{u}} \right)$$ | (20) |
| $$h _{u} =1.607\left( \frac{q ^{0.66} L ^{0.349}} {d _{m}^{0.34}} \right)$$ | (21) |
식 (21)을 수심-유량관계식으로 전환하면 식 (22)~(24)와 같다.
| $$h_u=5.8381\times q^{0.66},\;(L=1.0\;m,\;d_m=22.5\;mm)$$ | (22) |
| $$h_u=7.1296\times q^{0.66},\;(L=1.0\;m,\;d_m=12.5\;mm)$$ | (23) |
| $$h_u=10.7850\times q^{0.66},\;(L=1.0\;m,\;d_m=3.75\;mm)$$ | (24) |
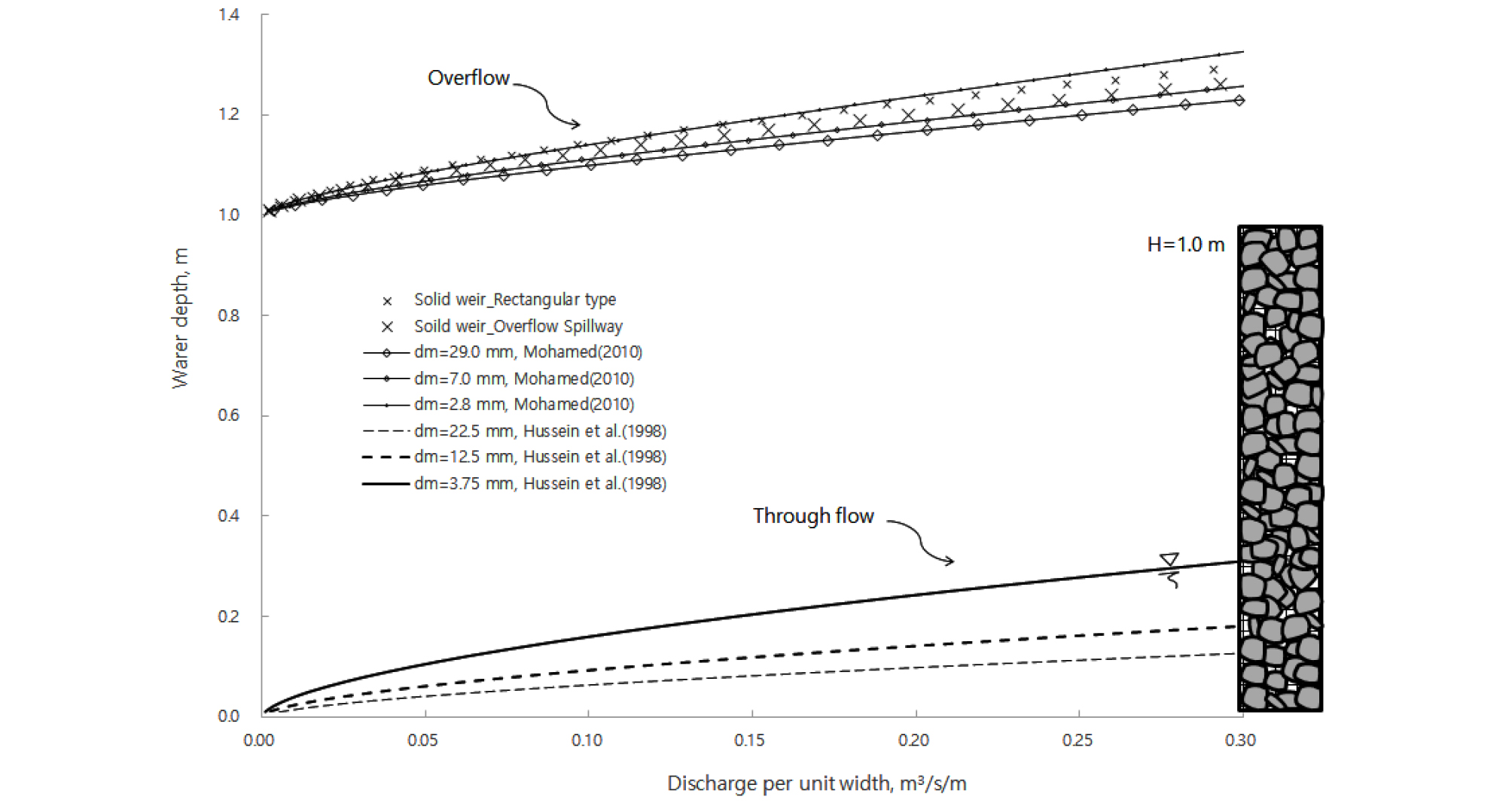
수심-유량 관계식으로 전환되기 위한 입력조건과 결과는 Table 1에 정리하였다. Fig. 3은 수심-유량 관계곡선들을 비교한 그림이다.
Table 1. Stage-discharge ratings of solid and gabion weirs
| Flow type | Weir | Input | H-Q rating | |||
| Overflow |
Solid weir
(Rectangular type) | 1.0 m | 1.0 m | 2.08~2.02 | ||
|
Soild weir
(Overflow spillway) | 1.0 m | 1.0 m | 2.21 | |||
|
Gabion weir
(Mohamed, 2010) | 29.0 mm | 1.0 m | 1.0 m | 3.61~3.65 | ||
| 7.0 mm | 1.0 m | 1.0 m | 3.01~2.23 | |||
| 2.8 mm | 1.0 m | 1.0 m | 2.42~2.51 | |||
| Through flow |
Gabion weir
(Hussein et al., 1998) | 22.5 mm | 1.0 m | |||
| 12.5 mm | 1.0 m | |||||
| 3.75 mm | 1.0 m | |||||
|
Gabion weir
(Mohamed and Mohamed, 2015) | 22.5 mm | 1.0 m | ||||
| 12.5 mm | 1.0 m | |||||
| 3.75 mm | 1.0 m | |||||
수심-유량관계식은 모든 경우에 거듭제곱형 곡선에 맞춤되었다. 콘크리트 보의 월류수심은 유량계수에 좌우되며, 유량계수가 가장 큰 값이 적용된 월류댐이 사각위어보다 작은 값을 보여주었다. 돌망태의 월류수심은 Mohamed(2010)의 실험에서 돌망태의 유량계수 값은 모든 경우에 콘크리트 보보다 값이 크며, 채움재의 평균입경이 클수록 커지고, 이 커질수록 감소한다고 하였다. 그러나 Fig. 3에서 보는 바와 같이, 채움재 입경이 2.8 mm의 경우, 유량이 0.15 m3/s/m보다 큰 값에서는 콘크리트 보보다 월류수심이 커지는 것으로 나타났다. 이러한 이유는 Mohamed(2010)의 실험에서 이 커질수록 유량계수 값이 감소하다가 다시 증가 하였기 때문인 것으로 보인다. 한편, 돌망태의 통과류에 관한 Hussein et al.(1998)의 식들은 에 영향을 받으며, 적용범위는 이다. 동일유량 조건에서 채움재의 입경이 작아질수록 상류수심의 값이 커짐을 확인할 수 있다(Fig. 3). Mohamed and Mohamed(2015) 실험에서는 수심과 유량은 선형관계였으나, 모형실험 규모보다 커짐에 따라 거듭제곱형으로 변하였으며, 계산된 수심 값은 보의 높이를 초과한 값을 보이며, Hussein et al.(1998)의 통과류보다 최대 10배 크게 계산되어 비교대상에서 제외하였다. 이와 같이 식 (16)~(18)은 의 적용범위 내에서 타당한 값을 보여주는 것으로 평가되어, 이 식들을 인공함양 Test bed 수계에 적용하여 돌망태 보의 저류성능을 검토하고자 한다.
수심-유량 관계식 적용
Test bed 현장개요
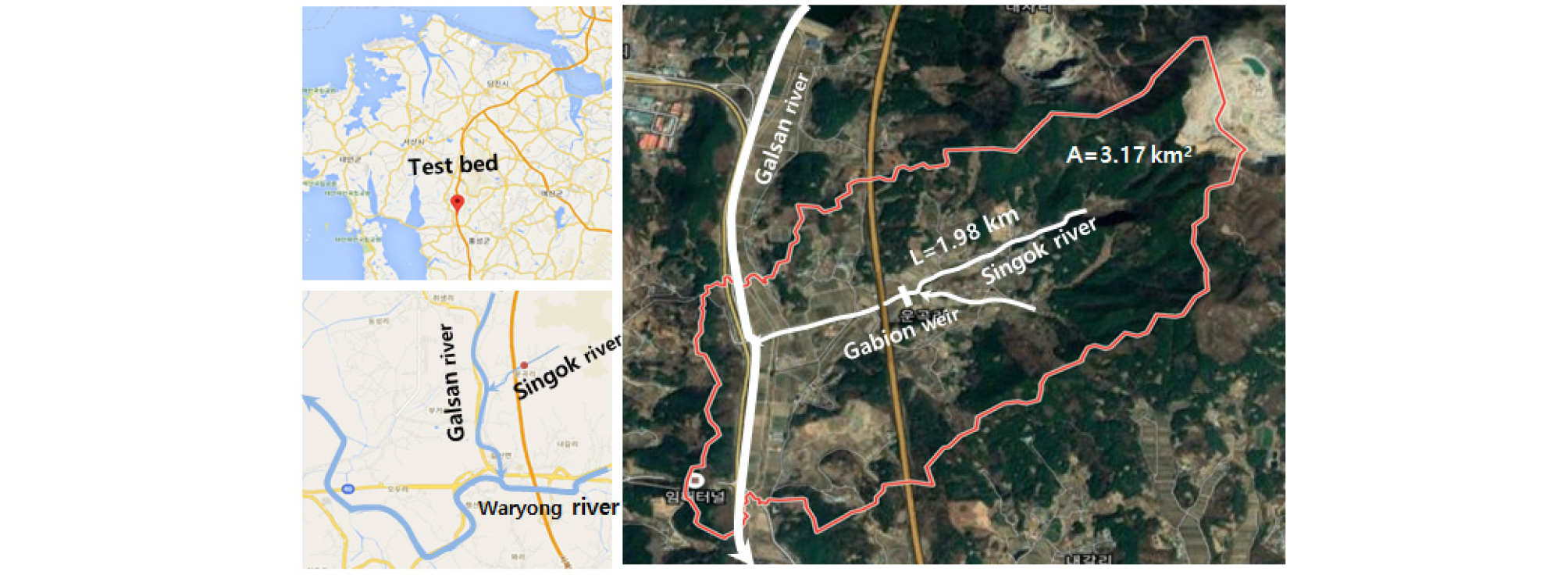
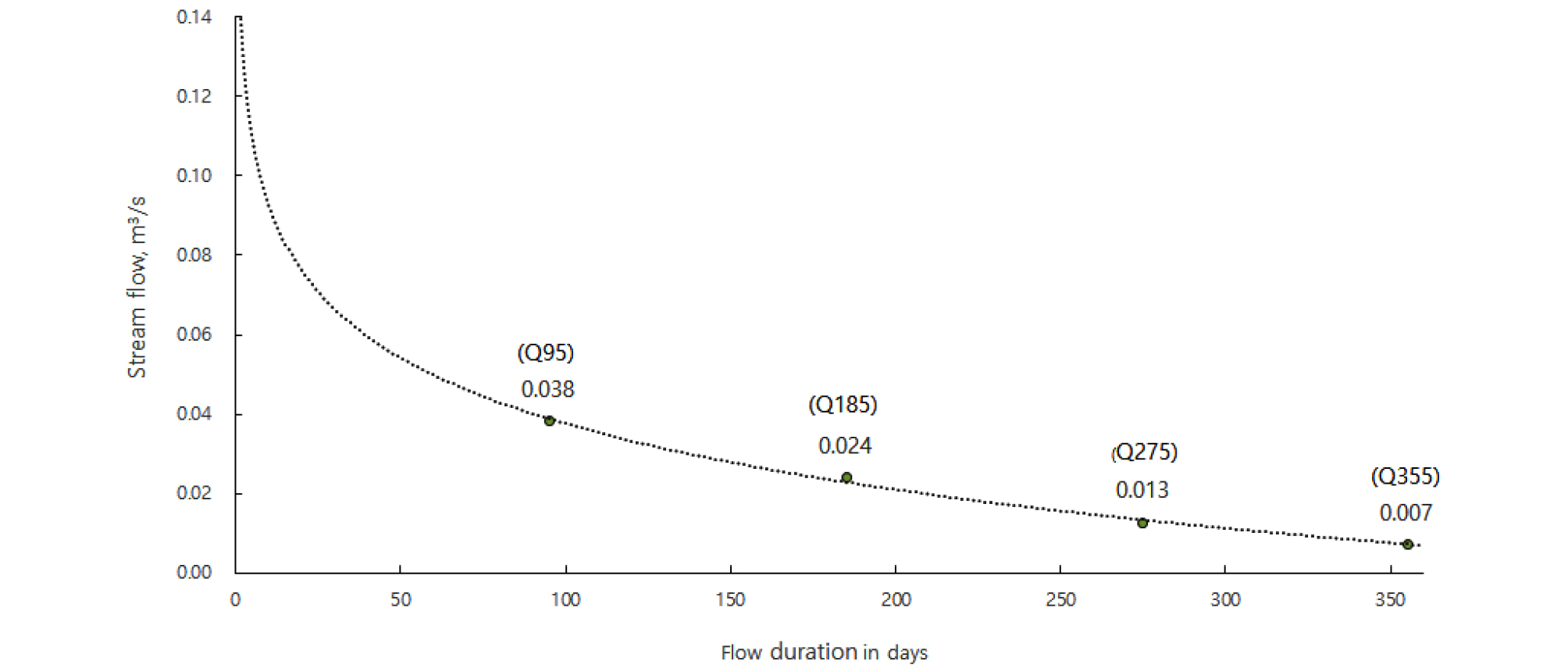
인공함양 Test bed의 행정구역은 충청남도 홍성군 갈산면 운곡리 일대이며, 유역면적은 3.17 km2이고, 산악과 구릉으로 연결된 지대이며, 산악이 기복된 사이에 좁은 들판을 이루고 있다. 분포지질은 신곡천 주변으로 충적층이 분포하고, 그 외 지역은 조립질 흑운모 화강암이 넓게 분포하고 있다. 신곡천은 본 유역의 유일한 소하천으로서, 총 연장 1.98 km, 하천 폭은 4.0~19.5 m이며, 서쪽으로 흐르다가 갈산천과 합류된다(Fig. 4). 일 유량의 연간상황을 나타내는 하천유황은 와룡천의 유황분석 자료(Hongseong County, 2011)를 이용하여 유량전이법으로 계산한 결과, 평균유량은 0.067 m3/s, 풍수량(95일)은 0.038 m3/s, 평수량(185일)은 0.024 m3/s, 저수량(275일)은 0.013 m3/s, 갈수량(355일)은 0.007 m3/s로 계산되었으며, Fig. 5에 나타내었다.
상류수심 및 취수율 계산
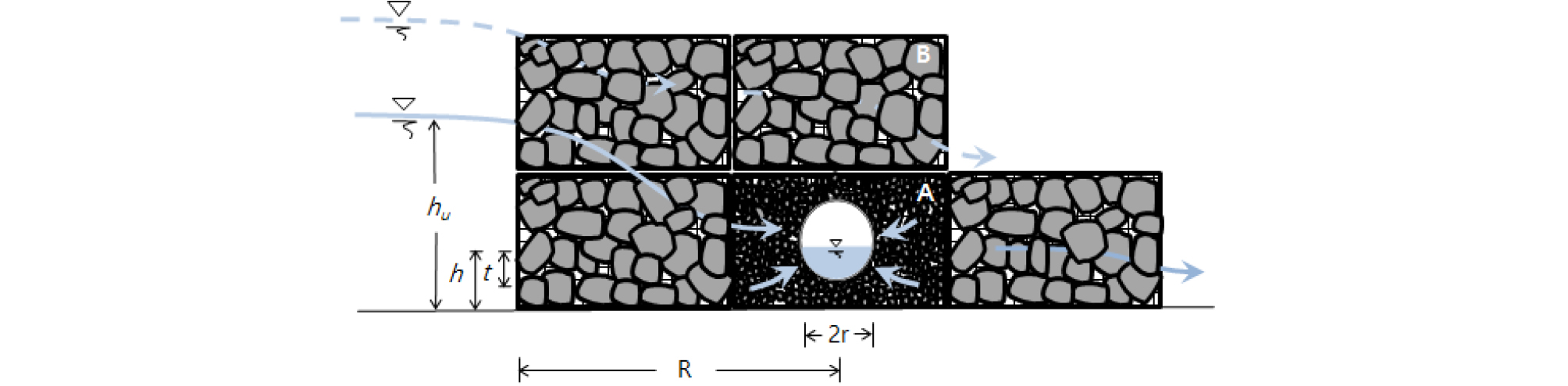
돌망태 보의 구조는 안정성 확보를 위하여 3열, 2단으로 구성하며, 하천수의 간접취수를 위하여 댐체 내에 유공취수관을 구비한다. 유공취수관 구역 A의 채움재는 상류수심 확보를 위하여 식 (16)~(18)에서 사용된 평균입경 크기가 3.75~22.5 mm인 작은 자갈로 하고, 그 외 구역 B의 채움재는 A구역보다 입경이 큰 자갈로 한다(Fig. 6). A구역의 투수계수는 식 (25)의 Hazen의 경험식(Geotechdata Info, 2013)을 이용하였다.
| $$k=cD _{10}^{2}$$ | (25) |
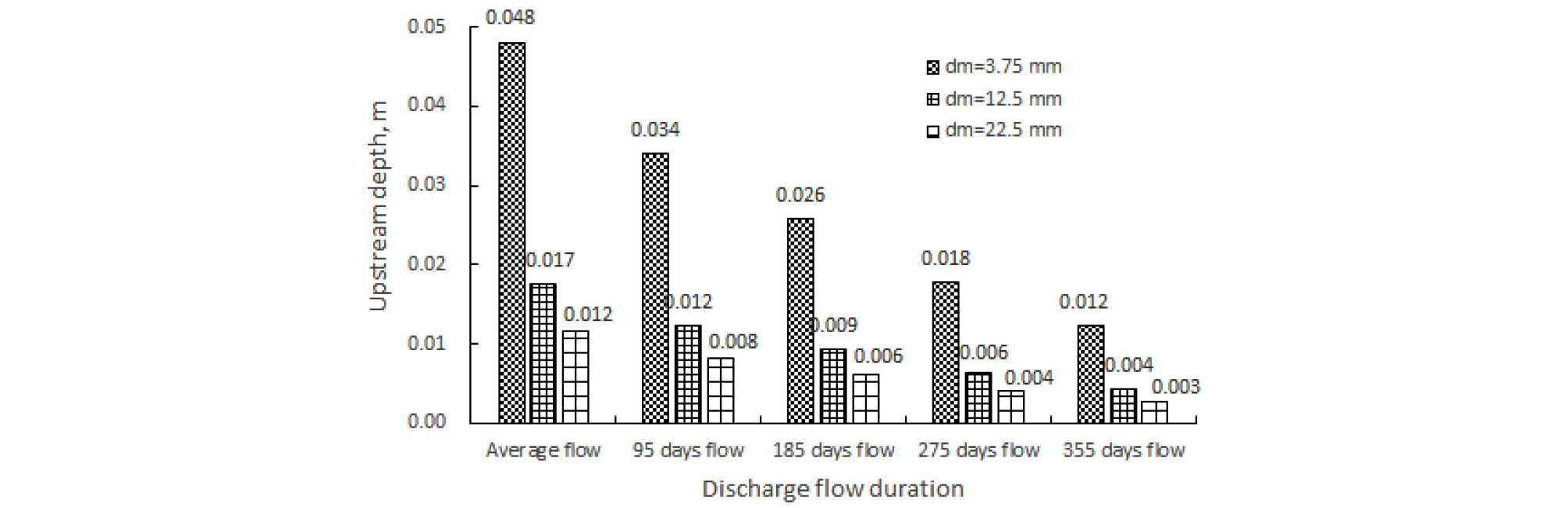
여기서, 의 상수, 은 유효입경이며, 투수계수는 입경별로 3.75 mm는 0.14 m/s, 12.5 mm는 1.56 m/s, 22.5 mm는 5.06 m/s가 계산되었다. 상류수심 계산은 식 (16)~(18)을 이용하였다. 상류수심은 채움재의 입경이 작을수록 큰 값을 보여주었으며, 채움재 입경 3.75 mm에서는 평균유량에서 0.048 m, 풍수량과 갈수량에서 각각 0.034 m와 0.012 m가 계산되었다. Fig. 7은 하천유황별 상류수심 계산 결과를 나타낸 것이다.
취수량은 집수매거 취수량 산출공식을 이용하였으며 식 (26)과 같다(Ministry of Environment, 2010).
| $$Q=\frac{k\times(h_u^2-h^2)\times b}R\times\sqrt{\frac{t+0.5\times r}h}\times\sqrt[4]{\frac{2h-t}h}$$ | (26) |
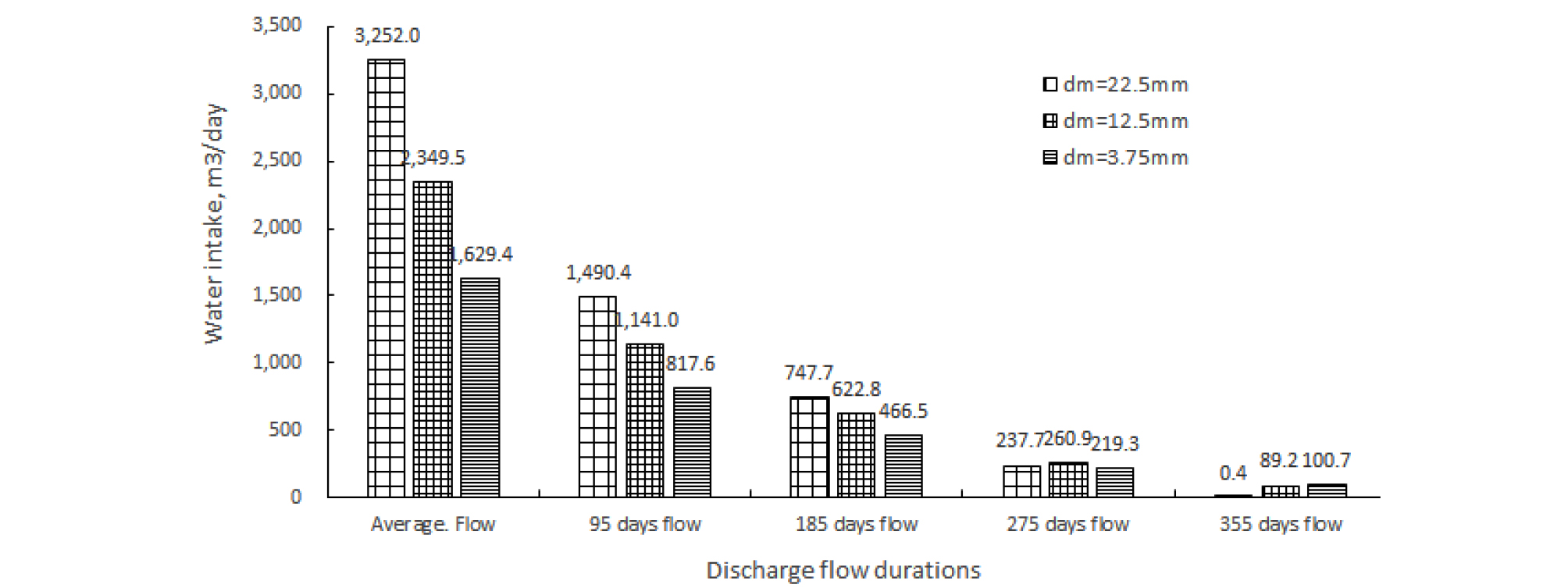
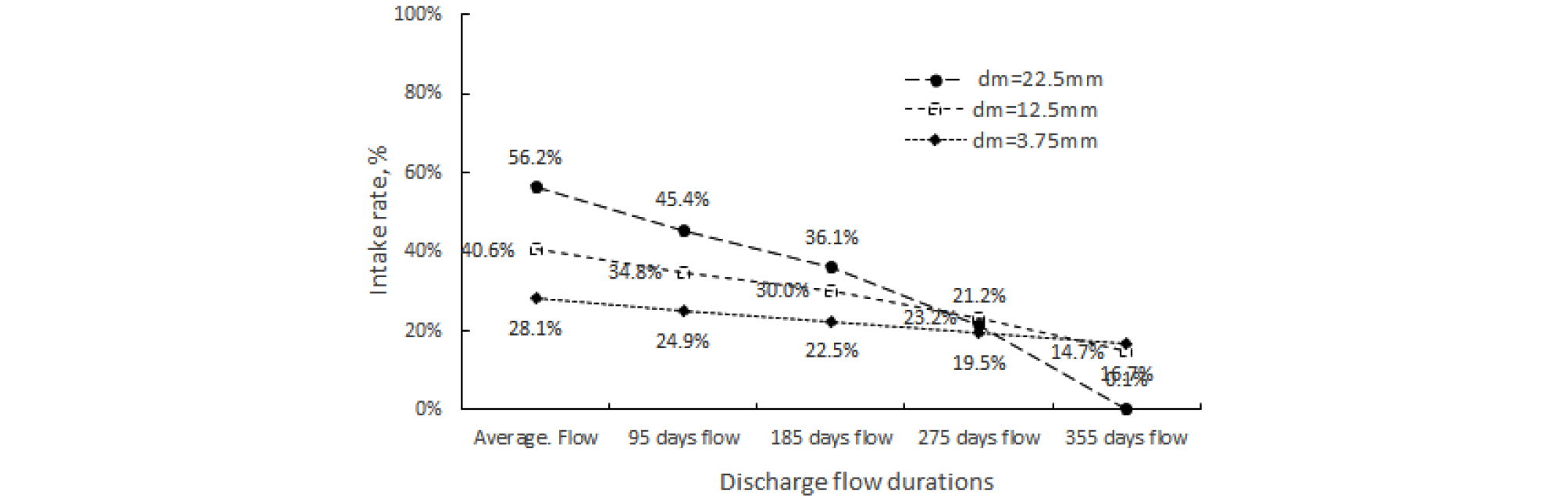
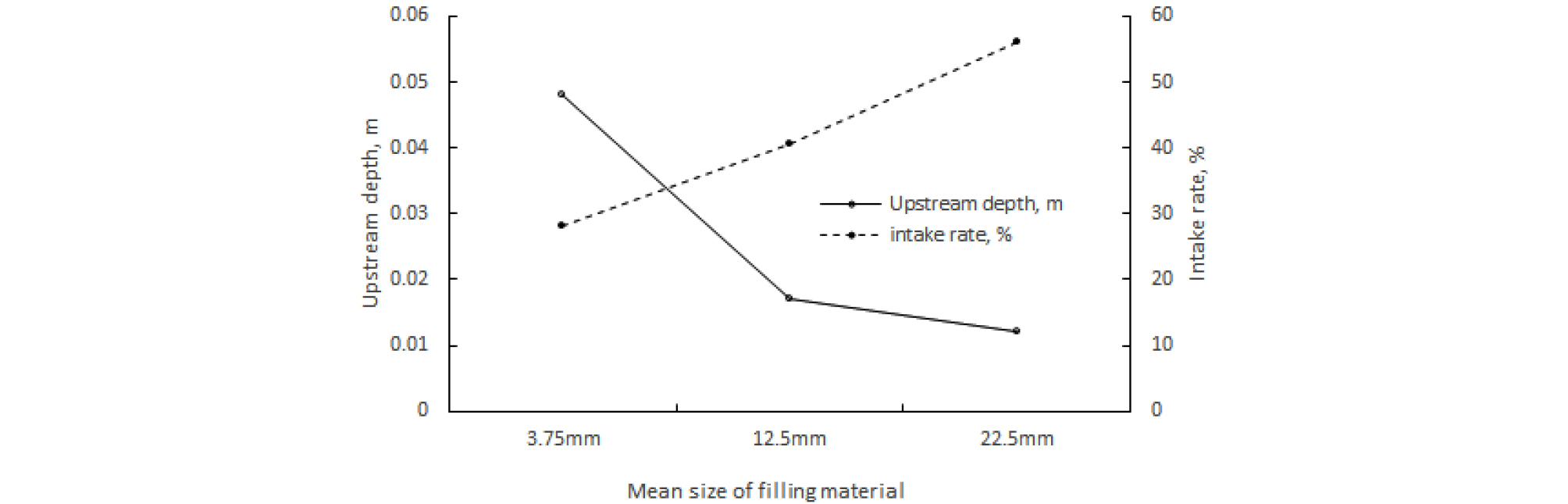
여기서, 는 취수량, 는 투수계수, 은 영향반경, 은 유공취수관의 반경, 는 유공취수관 내의 수위로부터 하천바닥까지의 깊이, 는 유공취수관 내의 수심, 는 유공취수관의 길이이다. 투수계수와 상류수심을 제외한 나머지 입력변수들은 취수량이 최대가 되도록 반복하여 값을 구하였다. 영향반경의 거리를 작게하고, 취수관을 바닥가까이 경사지게 설치하여 취수관 내 수심을 작게하므로서 수리경사가 커져서 취수량이 극대화되었다. 취수량은 상류수심과 달리, 채움재의 입경이 클수록 큰 값이 계산되었다. 이는 식 (26)에서 투수계수가 취수량에 가장 큰 영향을 미치는 변수이기 때문이다. 채움재 22.5 mm 입경에서 취수량은 평균유량에서 3,252.0 m3/day이며, 풍수량과 갈수량에서는 각각 1,490.4 m3/day, 0.4 m3/day이 계산되었다. 취수율은 평균유량에서 56.1%이며, 풍수량과 갈수량에서는 각각 45.4%, 0.07%가 계산되었다. Table 2와 Table 3에 각각 입력변수의 값과 계산결과를 정리하였으며, Fig. 8에 하천유황별 유량, 취수량을 나타내었고, Fig. 9에 하천유황별 취수율을 나타내었다. Fig. 10은 평균유량에서 계산된 상류수심과 취수율을 입경별로 도식화한 그림이다. 채움재의 입경이 커질수록 저류성능을 지시하는 상류수심은 작아지나, 취수성능을 지시하는 취수율은 증가하는 것을 알 수 있다.
Table 2. Input parameters
| 22.5 mm | 5.06 m/s | 0.45 m | 0.15 m | 0.0028 m | 0.0028 m | 10.0 m |
| 12.5 mm | 1.56 m/s | 0.45 m | 0.15 m | 0.0028 m | 0.0028 m | 10.0 m |
| 3.75 mm | 0.14 m/s | 0.45 m | 0.15 m | 0.0028 m | 0.0028 m | 10.0 m |
Table 3. Calculation results
결 론
돌망태 보 채움재의 물리적 특성을 실험변수들과 관계식으로 표현한 Hussein et al.(1998)의 방류량 산출식은 유량과 수심의 관계를 잘 표현하였으며, 이 식과 취수량 산출식을 이용하여 돌망태 보의 저류와 취수성능을 검토한 결과는 다음과 같다.
(1) 저류성능을 지시하는 수심은 채움재의 평균입경에 가장 큰 영향을 받는다. 평 균입경이 작아질수록 상류수심은 커진다. 평균유량 시에 채움재의 평균입경이 가장 작은 3.75 mm에서 0.048 m의 가장 큰 상류수심 값을 보여주었다. 돌망태 보는 투수성 댐체이므로 콘크리트 보보다 동일한 유량에서 낮은 수심을 형성하여 저류효과 측면에서 불리하다. 따라서 입경이 작은 채움재를 사용함으로서 콘크리트 보의 저류수준에 접근할 수 있을 것으로 보인다.
(2) 돌망태 보의 간접취수에 의한 취수율에 가장 큰 영향을 미치는 변수는 유공취수관 구역의 투수계수이며, 채움재의 평균입경이 작아질수록 투수성이 저감되어 취수율은 감소한다. 평균유량 시에 채움재의 평균입경이 가장 작은 3.75 mm에서 28.1%의 가장 작은 취수율을 보여주었다. 그러나 채움재의 평균입경이 일정크기 이상으로 커지면 하천의 유지수심에 문제가 발행할 수도 있다.
이와 같이 채움재의 평균입경은 돌망태 보의 저류와 취수성능에 가장 큰 영향을 미치는 인자이므로, 하천의 관리수심을 유지하면서 인공함양 원수의 수량을 확보하기 위해서는 최적의 채움재 평균입경크기가 선정되어야할 것이다.