서 론

암반은 보통 불균질하고 이방성이며 불연속적인 성질을 갖는다. 지질학적 의미에서 불연속면은 암반 내에 발달하는 단층(fault), 절리(joint), 층리(bedding), 엽리(foliation), 균열(crack), 틈(fissure), 깨짐(fracture) 등으로 표현할 수 있다. 이와 함께 공학적 의미에서는 암반 내에 존재하는 인장강도가 작거나 거의 없는 역학적 결함으로 암반에서 나타나는 모든 연약한 면을 총괄적으로 의미하기도 한다. 암반 내에 발달하고 있는 불연속면의 특성으로는 불연속면의 방향, 간격, 연속성, 간극, 충진물, 누수, 불연속면군의 수, 암괴의 크기 등으로 구분할 수 있다(Brown, 1981). 암반에 터널이나 사면과 같은 구조물이 건설될 때 암반의 거동은 불연속면의 존재 여부에 따라 크게 달라질 수 있다. 따라서 이들 암반 구조물에 대한 안정성을 정확하게 평가하기 위해서는 이들에 영향을 미칠 수 있는 불연속면의 상태를 세밀하게 파악하는 것이 중요하다.

절리면 강도에 대한 영향을 정량화하기 위하여 많은 연구자가 강도변수를 얻기 위한 여러 가지 변수 및 상관관계를 제안하였다(Patton, 1966; Barton et al., 1974; Barton and Choubey, 1977; Kulatilake et al., 1995; Cho et al., 2013; Lee et al., 2019). Patton(1966)은 응력 단계에 따라 거칠기 절리의 거동이 다르게 나타나는 실험 결과로부터 이러한 현상을 표현하는데 더 적합한 이중선형파괴기준식(bilinear failure criterion)을 제안하였다. Barton et al.(1974)은 Q-sytem에서 절리의 거칠기(joint roughness)와 절리의 변질(joint alteration)을 고려하여 점토물질이 충진된 불연속면의 강도를 산정하였다. Barton and Choubey(1977)는 절리면 거칠기 계수(Joint Roughness Coefficient, JRC)와 절리면 압축강도(Joint Compressive Strength, JCS)를 사용하여 충진물이 없는 절리의 마찰에 대한 상관관계를 제시하였다. Kulatilake et al.(1995)은 이방성 성질을 갖는 암반 절리에 대한 새로운 최대 전단강도 기준식을 제안하였다. Cho et al.(2013)은 절리면의 거칠기 변화가 전단강도에 미치는 영향을 조사하기 위하여 다단계 전단시험을 수행하여 거칠기 계수를 산정하고 미세 거칠기 빈도 변화를 조사하였다. Lee et al.(2019)은 직접전단시험, 기울임 시험, 당김시험을 실시하여 최적의 기본마찰각을 측정하고 정확하고 효율적인 시험방법을 제시하였다. 최근에는 개별요소법(Distinct Element Method, DEM)에 근거한 수치해석적인 방법을 사용하여 암석 절리면의 전단거동과 특성에 관한 연구가 활발히 진행되고 있다(Park and Ryu, 2005; Park and Song, 2009, 2013; Kim et al., 2012; Lazzari, 2013; Lambert and Coll, 2014; Chiu et al., 2016). Park and Ryu(2005)는 PFC2D를 이용하여 절리암반의 역학적 물성을 평가하는 연구를 수행하였다. Park and Song(2009, 2013)은 PFC3D의 결합-입자 모델을 이용하여 암석 절리에 대한 직접전단시험과 암석 절리의 접촉 면적을 수치해석적으로 모델링하는 연구를 수행하였다. Kim et al.(2012)은 PFC를 이용하여 표면 거칠기에 따른 입자와 비파쇄 평면과의 접촉면에서의 전단거동을 분석하여 입자 형상이 전단거동 특성에 미치는 영향을 확인하였다. Lazzari(2013)는 PFC2D를 이용하여 암석 절리의 전단강도를 분석하고 결정할 수 있음을 제시하였다. Lambert and Coll(2014)은 개별요소법을 사용하여 매끄러운 절리 접촉 모델을 모델링하였다. Chiu et al.(2016)은 거칠기 절리 모델을 이용하여 암석 절리 거동 모델링으로부터 거칠기가 암석 절리 거동에 미치는 영향을 규명하였다. 하지만 아직 Barton and Choubey(1977)가 제안한 절리면 거칠기 형태에 대한 비교 연구는 아직 미미한 실정이다.

이 연구에서는 암석 절리면 거칠기의 영향을 알아보기 위해 Barton and Choubey(1977)가 제안한 10가지 형태의 표준 절리 프로파일 중 절리면 거칠기가 편평하고 매끄러운 1번과 절리면 거칠기 진폭이 비교적 큰 7번과 9번에 대해 수치전단시험을 실시하였다. 수치전단시험은 개별요소법을 기반으로 하는 입자유동 해석 프로그램인 PFC2D(Particl Flow Code 2D, Itasca Consulting Group Inc., 2008)를 사용하였다. 수치전단시험 결과로부터 절리면 거칠기의 형태에 따른 응력-변위 관계를 분석하고, 이를 이용한 Mohr-Coulomb 파괴기준선을 이용하여 절리면 마찰각을 산정하였다. 최종적으로 PFC2D를 이용하여 절리면 거칠기 형상을 구현함으로써 절리면 거칠기가 전단거동에 미치는 영향을 살펴보았다.

절리 거칠기

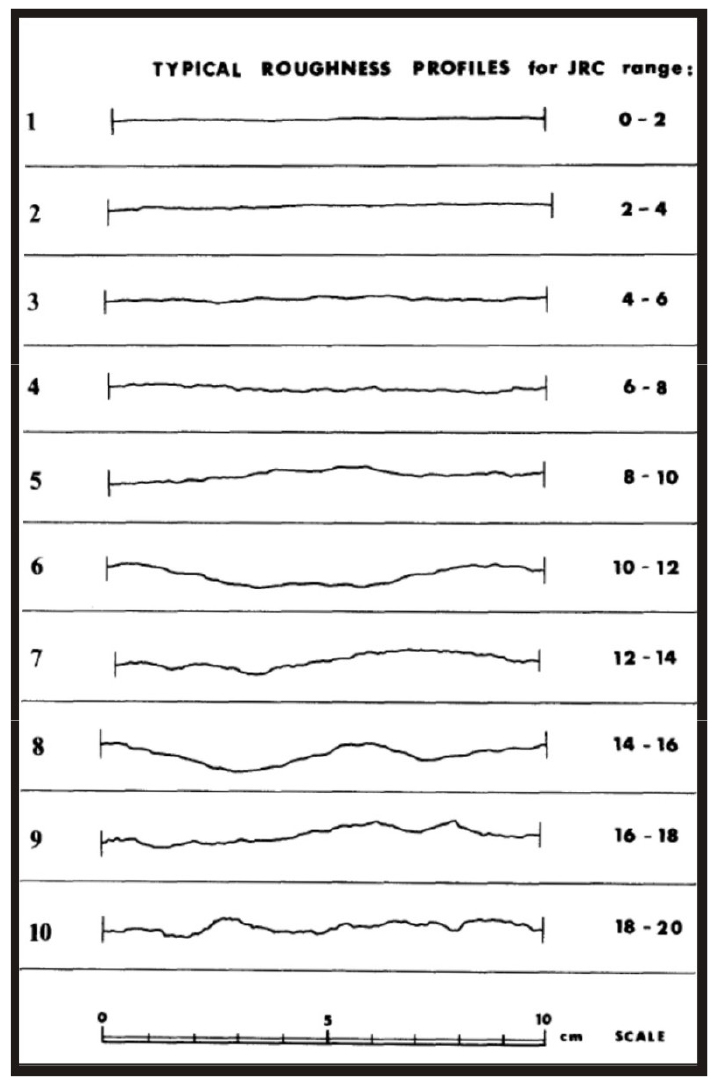
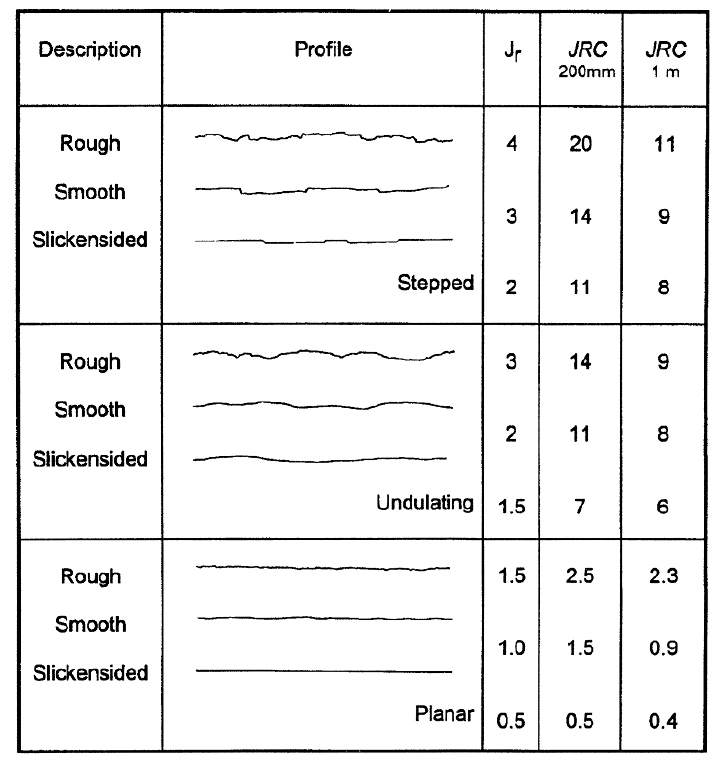
절리의 거칠기는 절리의 역학적 성질에 영향을 미치는 매개변수이며, 특히 절리의 전단강도 결정과 다양한 역학적 및 수리학적 성질의 특성을 결정하는 데 중요한 역할을 한다. 불연속면의 거칠기는 평균 평면에 대한 불연속면에 나타나는 작은 규모의 요철(uneveness)과 더 큰 규모의 만곡(waviness)으로 정의된다(Brown, 1981). 절리 거칠기 계수(JRC)는 Barton and Choubey(1977)가 제안한 10가지 형태의 표준 절리 프로파일 형상에 따라 0~20 사이의 값으로 표현되는 상대적 개념의 수치화된 계수이다(Fig. 1). Barton(1987)은 Q-system에서 주어지는 절리면 거칠기(Jr)와 블록 크기에 대한 JRC의 관계를 계단상(stepped), 기복상(undulating), 평탄상(planar) 등으로 구분하여 Fig. 2와 같이 제시하였다.

Fig. 1.

Roughness profiles corresponding the typical range of JRC values (Barton and Choubey, 1977).

Fig. 2.

Relationship between Jr in the Q-system and JRC for 200 mm and 1 m samples (Barton, 1987).

절리면 전단강도

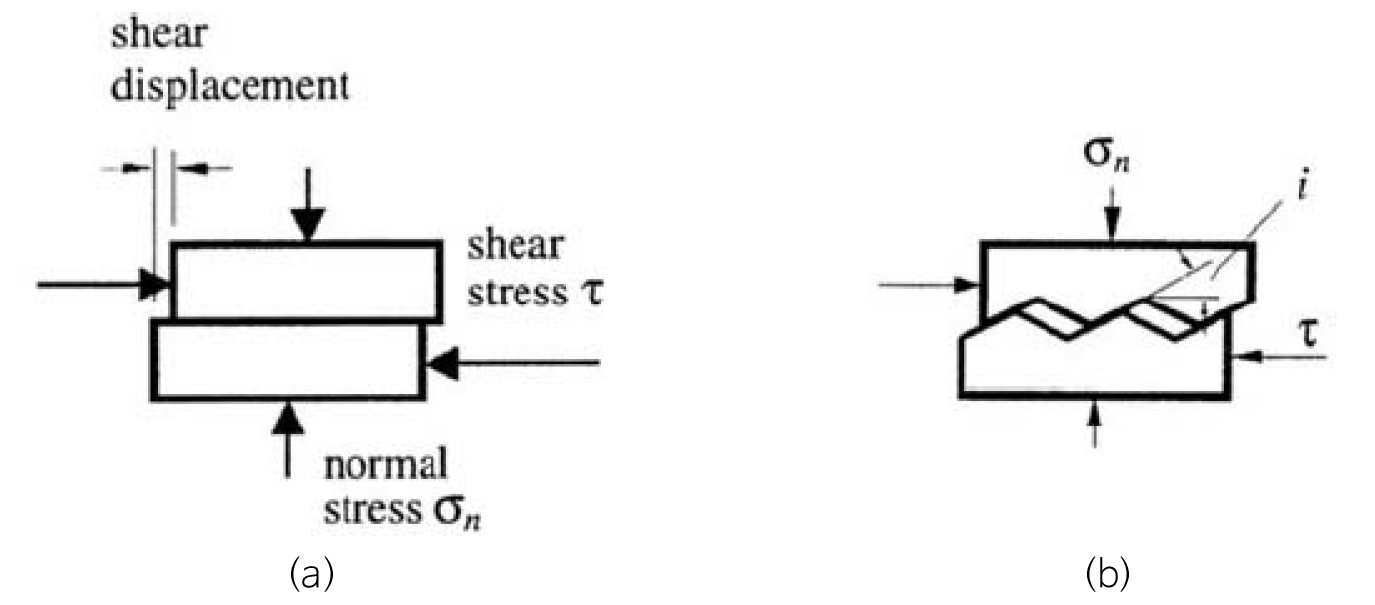
일반적으로 암석 표면 사이의 전단 저항은 두 가지 구성 요소에서 발생하는 것으로 알려져 있다. 그 하나는 두 암석 표면이 미끄러질 때 나타나는 마찰 성분과 다른 하나는 두 암석 표면의 기하학적 불규칙성으로 인한 미끄럼 저항이다. 절리면의 전단강도 크기는 암석 종류, 절리면 수직응력, 절리 충진물, 절리면 거칠기 등과 밀접한 관계를 갖는다. 예를 들면, 거칠기가 없는 신선한 암석 내 평편한 면에서의 전단강도(τ)는 식 (1)의 Mohr-Coulomb 파괴기준식으로 표현할 수 있다(Fig. 3a). 반면, 거칠기가 있는 절리면 전단강도는 Patton(1966)이 제시한 식 (2)의 파괴기준으로 표현된다(Fig. 3b).

여기서, c : 점착력(cohesion strength), σn : 수직응력(normal stress), ϕ : 마찰각(friction angle), ϕb : 기본마찰각(basic friction angle), i : 톱니면 각(saw-tooth face angle)

Fig. 3.

Shear strength of (a) planar surfaces expressed by the Mohr-Coulomb failure criterion and (b) rough surfaces expressed by the Patton failure criterion.

개별요소법 PFC2D

어떠한 대상을 개별적인 입자들의 집합체로 모델화하기 위하여 Cundall and Strack(1979)에 의해 개발된 개별요소법(Distint Element Method, DEM)은 입자 파쇄의 시각화를 구현하기 위해 널리 이용되고 있다. 개별요소법을 기반으로 하는 입자유동 해석 프로그램인 PFC2D(Particl Flow Code 2D)는 정적 및 동적 거동 문제를 해석하는데 유용하게 사용된다. PFC2D 모델링의 계산과정은 Fig. 4와 같이 시간 단계별 각 요소 입자의 운동방정식과 각 요소 입자간 접촉점에서 힘-변위 관계식의 반복적인 적용에 의해 변형과 파괴의 계산이 수행된다. 입자 형상은 원형 단일 입자 모델과 입자 결합 모델인 클럼프(clump) 및 클러스터(cluster) 모델로 나눌 수 있다. 입자 사이의 결합 형태는 입자 인접 요소 사이의 접촉점에서 일정한 수직 및 전단 강성의 스프링 거동을 갖는 접촉 결합(contact bond) 모델과 입자 요소가 구나 실린더 형태로 원이나 사각단면에서 접촉 거동을 갖는 병렬 결합(parallel bond) 모델로 나타낼 수 있다(Fig. 5).

Fig. 4.

Calculation cycle in PFC2D (redrawn from Itasca Consulting Group Inc., 2008).

Fig. 5.

Bonding logic of (a) contact bond and (b) parallel bond models in PFC2D (Itasca Consulting Group Inc., 2008).

접촉 결합 모델은 수직성분(normal component)와 전단성분(shear component)으로 나누어 계산된다. 접촉점에서 인장력이 수직방향의 결합강도인 인장강도에 도달하면 결합이 깨지고 수직 및 전단 접촉력은 상실된다(Fig. 6a). 전단 접촉력이 전단방향의 결합강도인 전단강도에 도달하면 결합은 깨지지만 접촉력은 그대로 존재한다(Fig. 6b). 그림에서 Fn은 수직 접촉력으로 Fn>0이면 인장, Un은 수직방향 상대변위로 Un>0이면 두 요소가 중첩됨을 의미한다.

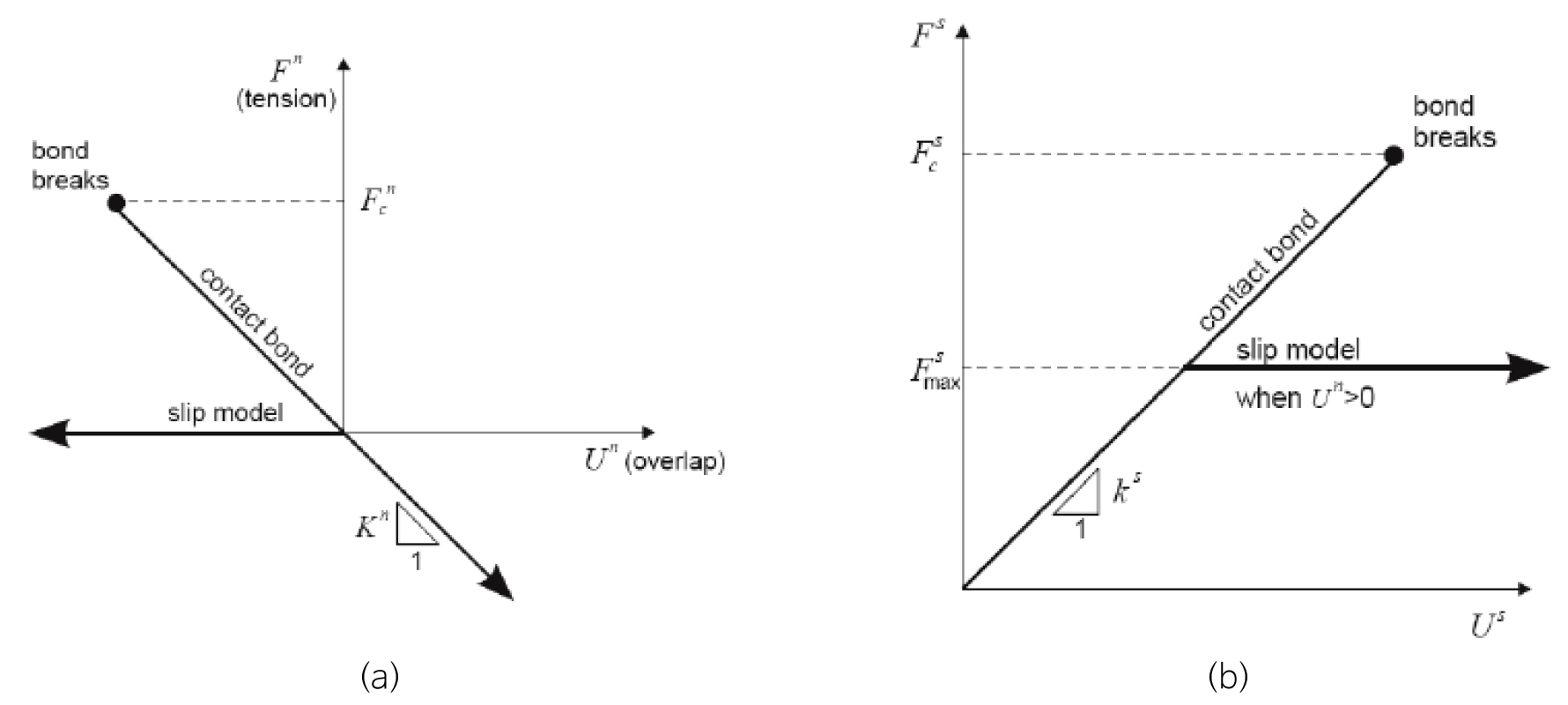
Fig. 6.

Constitutive behavior for contact occuring at a point (a) normal component and (b) shear component of contact force (Itasca Consulting Group Inc., 2008).

수치해석 모델

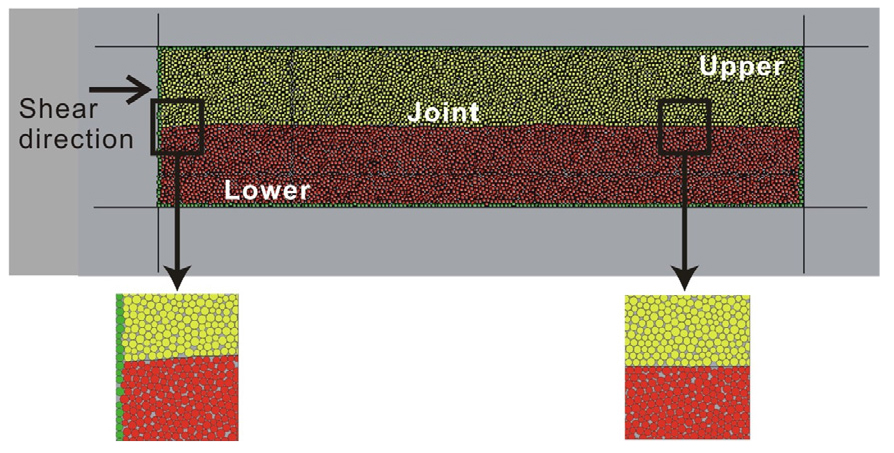
PFC2D에서 지원하는 입자는 2차원일 경우 단위 폭을 갖는 원기둥, 3차원일 경우 구로 간주되어 모델링 되며, 각 입자들에 물성이 부여된다. 입자에 관한 입력 변수는 입자의 밀도, 입자의 크기, 입자의 강성률, 입자 사이의 결합력 등이 있다. 이 연구에서 사용된 입자 형상은 원형 단일 입자 모델인 온볼(one ball) 모델을 사용하였다. 볼 입자의 크기는 절리면의 파괴양상을 세밀하게 관찰할 수 있도록 반지름을 0.15 cm로 하였다. 입자 밀도는 2,200 kg/cm³, 입자 강성률은 2.0, 입자 접촉 계수은 0.18 GPa, 접촉 결합 수직 및 인장강도는 18 MPa로 선정하여 전단거동을 분석하였다. 수치전단시험에 사용된 거칠기는 거칠기 정도를 고려하여 Barton and Choubey(1977)가 제안한 10가지 형태의 표준 절리 프로파일 형상 중 JRC 0~2에 속하는 1번, JRC 12~14의 7번, 그리고 JRC 16~18의 9번 등 3가지로 선정하였다(Fig. 1). PFC2D 모델의 전단박스의 크기는 폭 100 mm, 높이 25 mm로 모델링하였다(Fig. 7). 모델에서 하부벽은 움직임에 제한을 두도록 고정시키고, 상부벽은 상하로 이동이 자유롭게 하여 우 측으로 이동시킴으로써 접촉면에서의 전단이 발생하도록 하였다. 이때 수직응력은 서보 컨트롤 시스템(servo-controlled system, Itasca Consulting Group Inc., 2008)에 의해 일정하게 유지하도록 하였다.

Fig. 7.

PFC2D model for numerical shear testing.

PFC2D 수치전단시험 결과

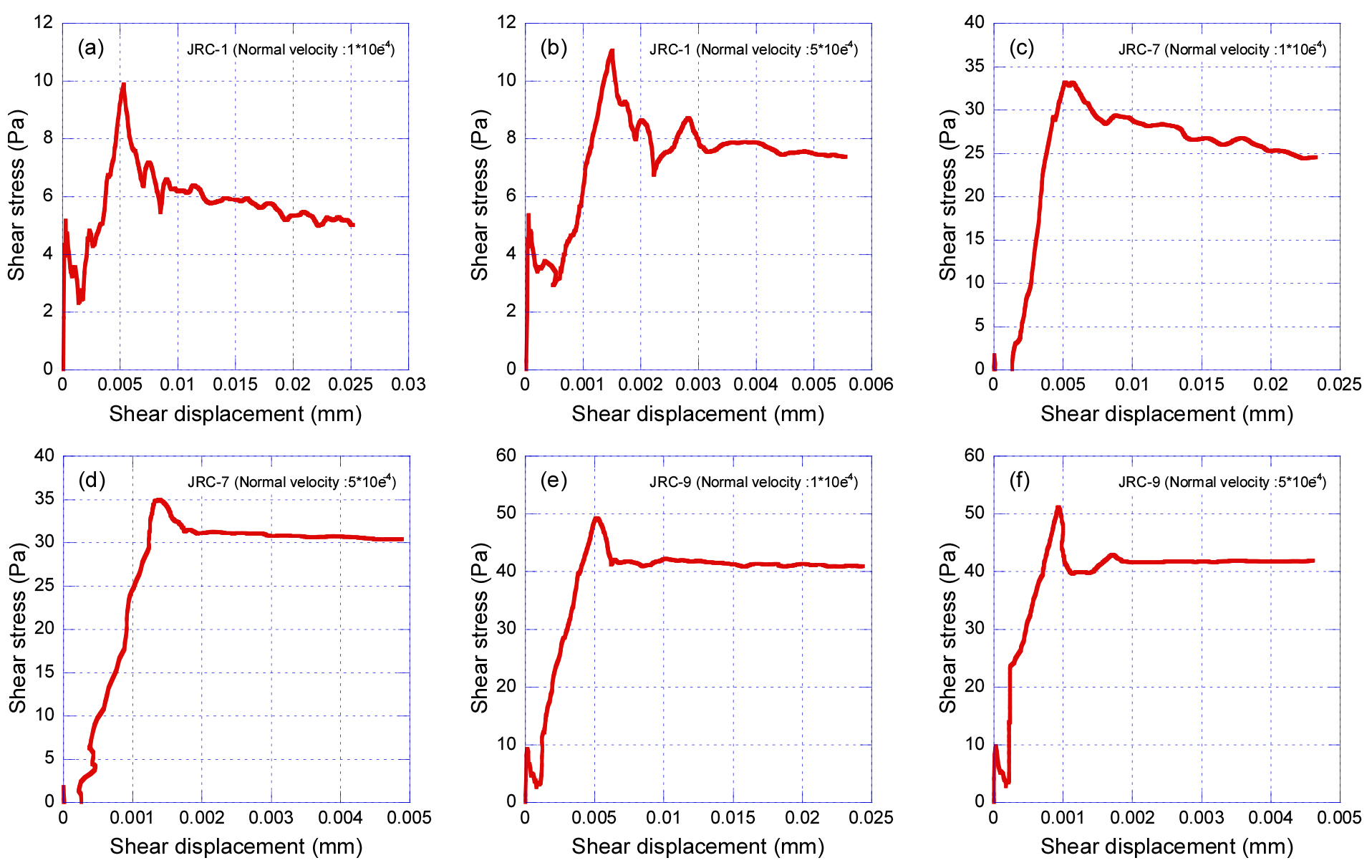
Fig. 8은 Barton and Choubey(1977)가 제안한 10가지 형태의 표준 절리 프로파일 중 수치전단시험을 실시하기 위한 선정된 1번, 7번, 9번에 대한 PFC2D 모델을 보여준다. 그림에서 보는 바와 같이 모델 JRC-1은 절리면이 매끈하고 진폭이 거의 없는 반면, JRC-7과 JRC-9는 거칠고 진폭도 매우 큼을 알 수 있다. 각각 3의 모델을 대상은 같은 조건에서 PFC2D 수치전단시험을 수행하였다.

Fig. 8.

PFC2D model for numerical shear testing on JCR-1, JCR-7, and JCR-9 suggested by Barton and Choubey (1977).

수치전단시험 결과로부터 전단응력-전단변위 관계를 그래프로 나타내면 Fig. 9와 같다. Figs. 9a, 9b의 거칠기 진폭이 거의 없는 매끄러운 평면를 나타내는 JRC-1의 경우, 전단변위에 따른 전단응력이 매우 불규칙하게 움직이는 것을 볼 수 있다. 반면 Figs. 9c~9f의 거칠기 진폭이 큰 JRC-7과 JRC-9의 경우, 전단응력이 최대값에 도달한 이후에 일정한 값으로 수렴하는 것을 알 수 있다. 최대 전단응력의 경우, 모델의 거칠기 정도와 상관없이 첫 번째 수직응력보다 두 번째가 더 큰 최대 전단응력을 나타냈다. 하지만 그 차이는 매우 미미함을 알 수 있다. 최대 전단응력의 크기를 보면, 접촉면의 거칠기 진폭이 큰 JRC-7이 편평하고 매끄러운 JRC-1보다 약 3.2~3.4배, JRC-9은 약 4.6~5.0배 크게 나타났다(Table 1). 즉, Barton and Choubey(1977)가 제안한 절리면의 거칠기가 커질수록 최대 전단응력은 증가하는 것으로 나타났다. 최대 전단변위의 경우, 첫 번째 수직응력일 때가 두 번째일 때보다 약 4.1~5.8배 더 크게 나타남을 알 수 있다.

Fig. 9.

The relationship between shear stress and shear displacement obtained from numerical shear tests by PFC2D: (a) first and (b) second of JRC-1, (c) first and (d) second of JRC-7, and (e) first and (f) second of JRC-9.

Fig. 10은 첫 번째 및 두 번째 수직응력 하에서 실시한 수치전단시험으로부터 얻은 최대 전단응력과 최대 수직응력을 그래프상에 표시한 것이다. 이 그래프를 이용하여 절리면 거칠기에 따른 절리면 마찰각을 산정하였다. 그림에서 보는 바와 같이 거칠기 진폭이 증가함에 따라 마찰각이 증가하는 경향을 보임을 알 수 있다. 절리면 마찰각의 크기는 접촉면의 거칠기 진폭이 큰 JRC-7이 접촉면이 편평하고 매끄러운 JRC-1보다 약 1.8배, JRC-9는 약 3.9배 정도 더 크게 나타났다(Table 1). 결과적으로 절리면에서 입자와 평면과의 접촉면에서 입자의 맞물림 현상은 절리면 거칠기 진폭이 클수록 증가하기 때문에 절리면 거칠기가 매끈한 경우보다 거친 경우가 절리면 마찰각을 크게 만드는 요인인 것으로 판단된다.

Fig. 10.

The relationship between shear stress and normal stress obtained from the numerical shear tests by PFC2D: (a) first and second of JRC-1, (b) JRC-7, (c) JRC-9, and (d) all.

결 론

암석 절리면 거칠기의 영향을 알아보기 위해 Barton and Choubey(1977)가 제안한 10가지 형태의 표준 절리 프로파일 중 절리면이 매끄러운 1번(JCR-1)과 거칠은 7번(JCR-7)과 9번(JCR-9)에 대해 입자유동 해석 프로그램인 PFC2D를 사용하여 수치전단시험을 실시하였다. 그 결과를 정리하면 다음과 같다.

최대 전단응력은 모델의 거칠기 정도와 상관없이 첫 번째 수직응력보다 두 번째가 더 큰 최대 전단응력을 나타냈으며, 그 크기는 절리면의 거칠기 진폭이 큰 JRC-7이 편평하고 매끄러운 JRC-1보다 약 3.2~3.4배, JRC-9은 약 4.6~5.0배 크게 나타났다. 최대 전단변위는 첫 번째 수직응력일 때가 두 번째일 때보다 약 4.1~5.8배 더 크게 나타났다. 절리면 마찰각의 크기는 접촉면의 거칠기 진폭이 큰 JRC-7이 접촉면이 편평하고 매끄러운 JRC-1보다 약 1.8배, JRC-9는 약 3.9배 정도 더 크게 나타났다. 이것은 절리면에서 입자와 평면과의 접촉면에서 입자의 맞물림 현상은 절리면 거칠기 진폭이 클수록 증가하기 때문에 절리면 거칠기가 매끈한 경우보다 거친 경우가 절리면 마찰각을 크게 만드는 요인인 것으로 판단된다.