서 론

지하에 작용하는 응력은 지진 발생 메커니즘 연구나 지하공간 개발의 안정성 분석을 위해 알아야 할 필수 요소이다. 보통 깊은 심도에서 발생하는 지진 발생 메커니즘을 규명하기 위해서는 광역적 응력장에 대한 자료가 필요하며 지진 단층면해(focal mechanism) 자료의 역산 등의 방법을 통해 해당 지역의 대표 응력 정보를 도출한다(Gephart and Forsyth, 1984; Michael, 1987). 지질공학 안정성 분석을 위해서는 비교적 천부 심도에 대한 국지적인 응력 특성이 요구되며, 보통 시추공에서 공학적 방법을 통해 규명된다. 시추공에서 실시되는 대표적인 응력 측정법에는 시추공의 격리된 한 구간에 수압을 가하여 공벽 암반을 파쇄시키는 수압파쇄법(Haimson and Cornet, 2003)과 지중응력에 기인하여 형성되는 시추공벽 압축파쇄대(borehole breakouts)를 감지하여 응력의 방향과 크기를 유추하는 방법(Zoback et al., 2003)이 있다.

응력은 흔히 암반 물성 불균질성, 단층/균열 등의 불연속면 등 다양한 요소에 의해 국지적으로 복잡하게 교란되는 것이 보통이다(Reiter, 2021). 시추공에서 규명된 응력은 종종 광역적, 대표적 응력장(원거리 응력)과 일치하지 않을 수 있으며 이에 대한 과학적 해석이 동반되지 않으면 응력 자료에 대한 신뢰성을 보장받기 어렵다. 특히 단층과 균열 등 불연속면은 지하에 산재해 있으며 지질공학적 안정성에 영향을 미칠 뿐 아니라 응력 교란에도 크게 영향을 미친다.

단층/균열에 의한 응력장 교란은 여러 형태의 수치모델로 유추하기도 한다(Homberg et al., 1997; Choi et al., 2021; Jang et al., 2022). 불연속면을 수치모델에서 구현하는 방식에는 크게 두 가지 기법이 있다. 하나는 불연속면을 얇은 매질로 구현하여 암반과 다른 물성이나 유변학적 특성을 부여하는 연속체 모사 방법이고, 또 하나는 두 암반이 접촉하는 불연속적 마찰면으로 모사하는 방식이다(Treffeisen and Henk, 2020). 전자는 보통 유한요소법(finite element method)에서 활용되며 후자는 개별요소법(discrete element method)에서 주로 활용된다. 이러한 수치모델을 위한 다양한 상용소프트웨어가 존재하여 통상적으로 활용되고 있다.

본 연구에서는 단층이나 균열 등의 불연속면을 상기한 두 가지 기법으로 모사할 때 응력 교란 결과에 어떤 차이가 나는지 비교하였으며, 실제 관찰된 응력 교란 양상과 비교하여 어느 기법이 응력 교란 모델링에 더 효과적인지 알아보고자 한다. 두 기법 모두 장단점이 있으며, 분석 목적에 따라 성능이 다양하게 나타나므로 어느 한 기법이 절대적으로 우월한 것은 아니다. 또한 주어진 한 기법에서도 섬세한 모델링 기술을 적용하여 모델 결과를 실제 관찰 결과와 유사해지도록 접근시킬 수도 있다. 본 연구에서는 단순한 2차원 단층 모델과 3차원 균열에 의한 시추공벽 응력 모델의 두 사례에 대해, 상기한 두 기법으로 불연속면을 모사할 때 응력 교란이 어떻게 모사되는지 비교하였다. 이를 위해 매우 단순하지만, 원천적인 차별성만을 강조하여 수치분석을 수행하였다. 본 연구에서는 상용소프트웨어인 콤솔멀티피직스를 이용하여 수치분석하였다.

2차원 단층 모델

모델 설정

단층은 보편적으로 전단운동이 집중되는 비교적 얇은 두께의 단층핵과 그 주위를 감싸는 비교적 두꺼운 단층손상대로 구성된다(Caine et al., 1996). 단층 모델링은 수치분석의 관심 영역과 모델의 규모에 따라 개별 단층 요소들을 모두 포함하여 모델을 구축할 수도 있고, 단순화된 하나의 불연속면 요소로 모델을 구축할 수도 있다. 본 연구에서는 지역적 응력 교란 패턴을 모사하기 위하여 단순화된 하나의 요소로 단층을 모사하였다.

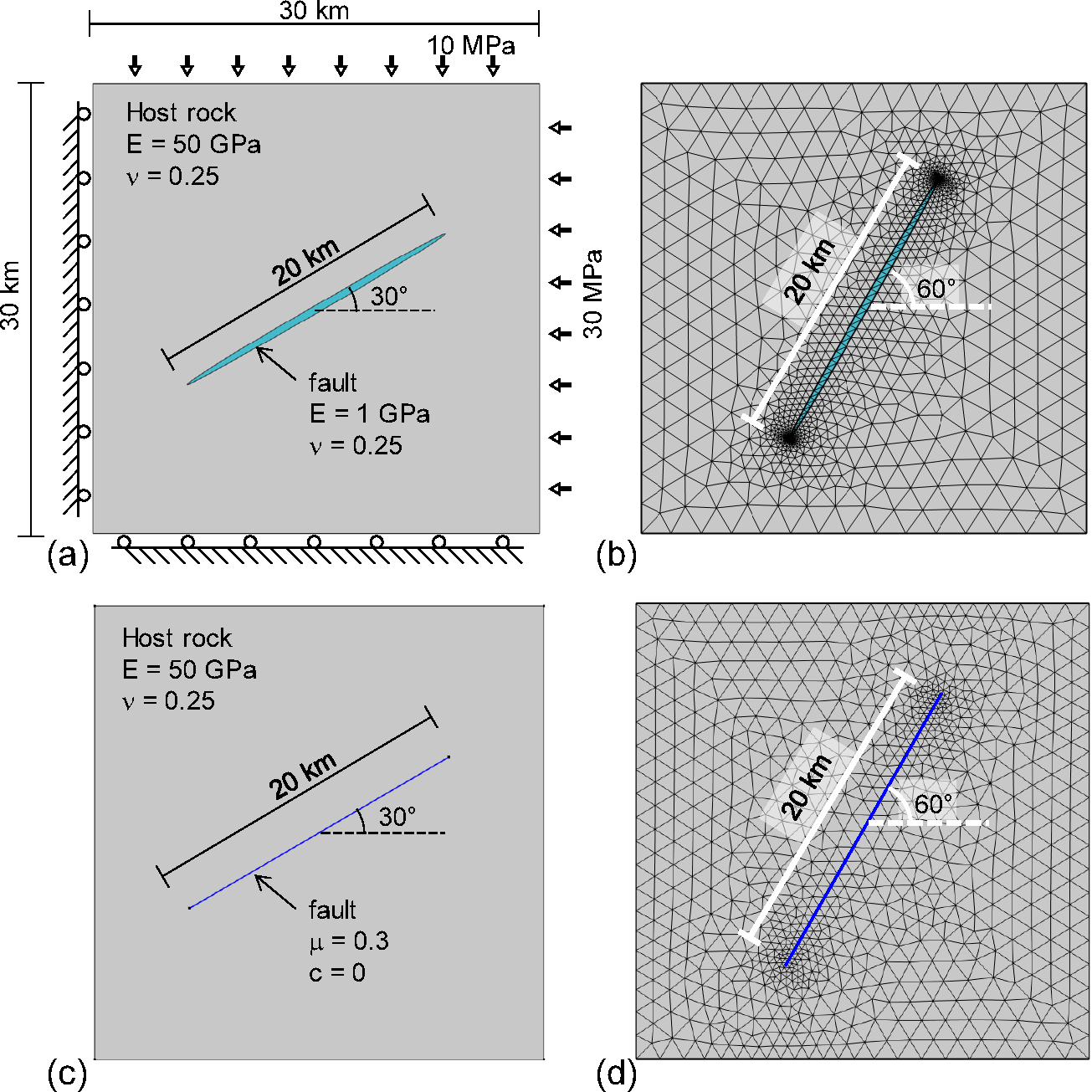
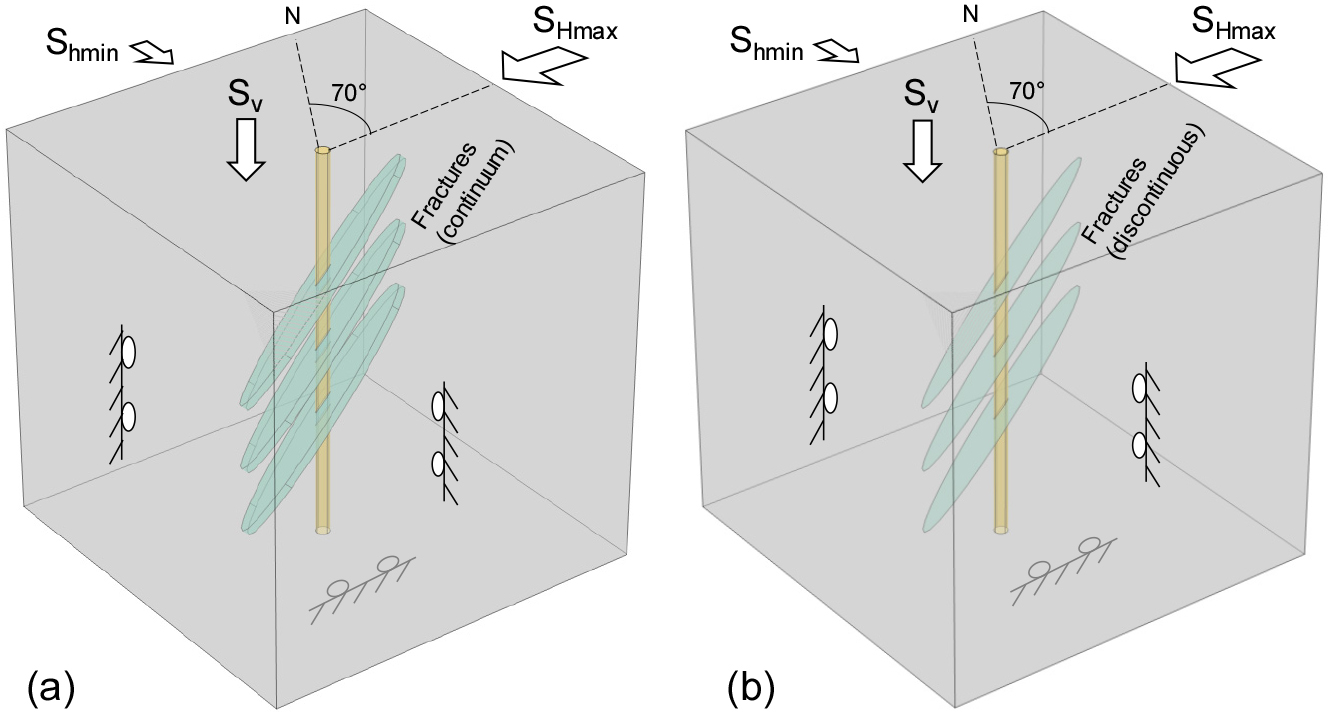
첫 번째 단층 모사 방법은 모암과 물성이 다른 얇은 물질로 단층을 구현하는 연속체 역학 방법이다. 분석될 2차원 모델은 크기 30 km × 30 km의 정사각형 모암 내에 길이 20 km의 얇은 단층 요소로 구성되었다(Fig. 1a and b). 2차원 단층의 형태는 타원 형태로 모사하였다(즉, 장축의 길이 20 km, 단축의 길이 0.1 km). 단층의 제원(특히 두께)에 따라 단층 주위 응력 교란 영역의 범위에 차이가 발생하나 이용된 단층의 두께(0.1 km)는 추후 비교할 실제 자료와 유사한 결과를 얻도록 임의로 지정한 값이다. 모암과 단층 물질은 모두 선형탄성, 균질성, 등방성 물질로 가정하였으며, 응력에 따른 변형을 조절하는 주요 물성인 영률은 모암 50 GPa, 단층 물질 1 GPa로 가정하였다(Gudmundsson, 2004). 모델링에서 큰 효과를 보이지 않는 포아송비는 모암과 단층 모두 0.25로 가정하였다. 모델은 2,000여개의 삼각형 격자 요소로 구성하였으며 불연속면 근처에서 더욱 조밀하게 격자화 되도록 구현하였다(Fig. 1b). 모델의 경계 조건은 모델의 좌단과 하단으로의 변위를 고정하는 롤러 경계 조건을, 우단과 상단으로는 각각 30 MPa, 10 MPa의 압축응력 경계 조건을 부여하였다. 가해진 응력 경계 조건은 추후 비교할 실제 자료의 경우와 유사한 응력 조건이다. 단층의 방향에 따른 차이를 관찰하기 위하여 단층 방향은 두 다른 방향(즉, 경계 조건으로 주어진 최대주응력 방향과 각각 30°와 60°의 방향)으로 모사하였다(Fig. 1a and b). Fig. 1a의 단층은 전단운동 하기에 유리한 방향의 단층, Fig. 1b의 단층은 전단 가능성이 낮은 단층으로 여길 수 있다. 주어진 응력 조건에서 단층의 전단 가능성은 전단성향으로 표현할 수 있는데, 이는 단층면에 작용하는 전단응력과 수직응력의 비로 표현된다. 주어진 경계 응력 조건에서 단층면에 투영되는 전단응력(𝜏)과 수직응력(σn)은 각각 식 (1a)와 (1b)로 표현된다.

여기서, σ1은 최대주응력, σ2는 최소주응력, 𝜓는 최대주응력 방향과 단층 극점의 각도이다. Fig. 1a와 b에 보인 단층의 전단성향(τ/σn)은 원거리 응력으로 계산하면 각각 0.58과 0.35이다.

Fig. 1.

Representation of a fault in 2D numerical models. In (a) and (b), a fault is represented by a weaker material with a lower Young’s modulus (E) compared with the host rock. In (c) and (d), a fault is represented by a discontinuous contact plane controlled by friction (𝜇).

두 번째 단층 모사 방법은 모암 내에 암석을 가르는 불연속면으로 구현하는 방법으로 불연속면 양쪽 암반에 전단 이격이 가능한 접촉면으로 정의된다. 이 경우 단층의 거동은 보통 Coulomb의 마찰법칙(식 (2))으로 조절된다.

여기서, c는 단층의 점착력, 𝜇는 마찰계수, σn은 단층면에 작용하는 수직응력, τc는 단층에 미끌림이 발생하는 임계 전단응력이다. 단층의 마찰계수는 단층 물질 조성에 따라 0.1~1.2의 폭넓은 범위를 보이는 것으로 알려져 있다(Moon et al., 2017). 본 모델에서는 단층의 유동성을 높이고자 마찰계수 0.3, 점착력은 0으로 부여하였다. 모암의 물성과 경계 조건 등 다른 모든 특성은 연속체 모델의 경우와 동일하다(Fig. 1c and d).

모델 결과

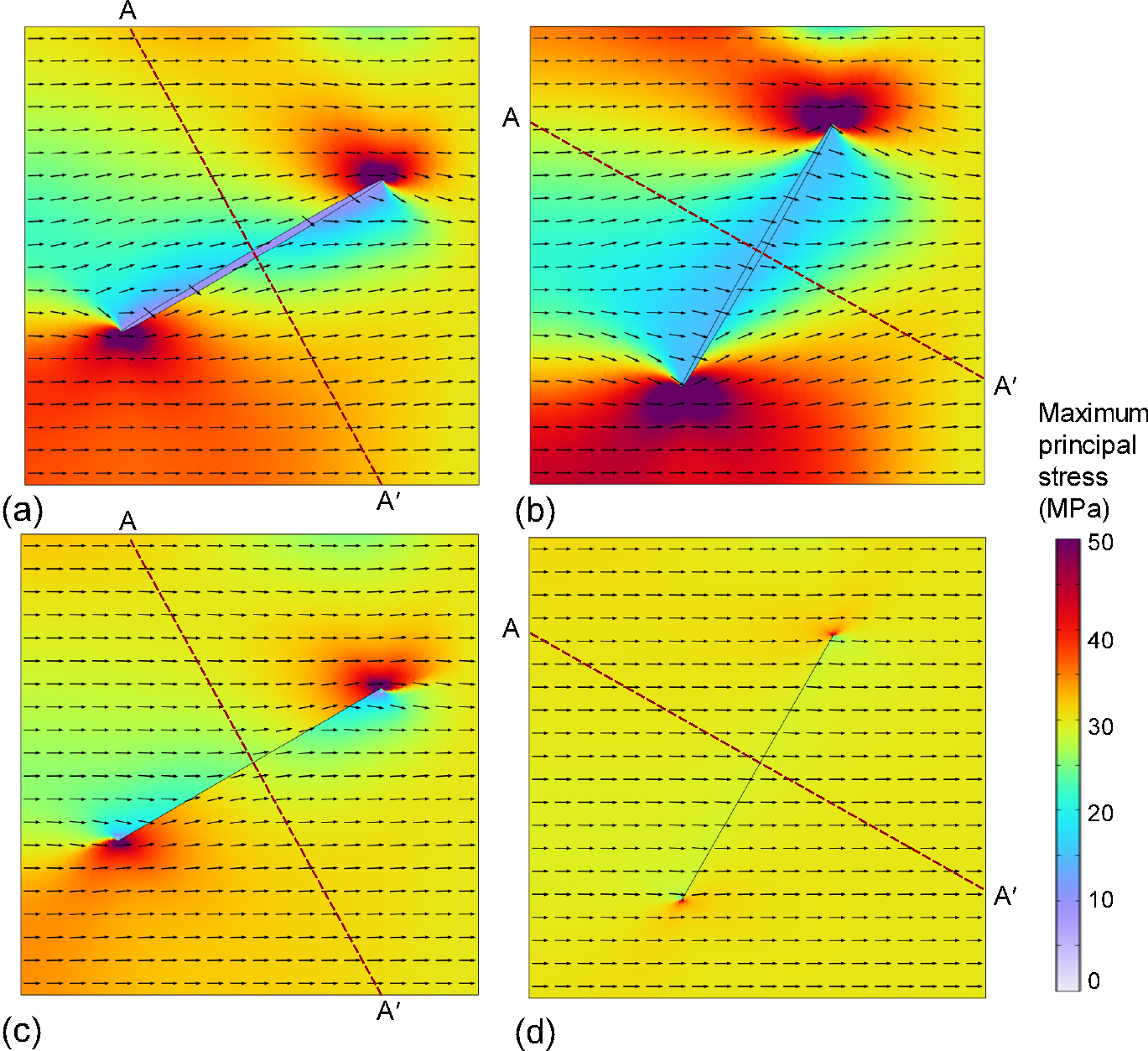
모델링 결과는 단층 주변으로 주응력의 방향 회전과 주응력의 크기 변화에 초점을 맞춰 분석하였다. Fig. 2는 모델 내 최대주응력의 방향을 선의 방향으로, 최대주응력의 크기를 색으로 도시한 결과를 보여준다. 연속체 모델의 경우(Fig. 2a and b) 단층 주변에서 최대주응력의 방향이 경계조건으로 주어진 방향으로부터 현저히 회전된 양상을 보인다. 그러나 단층 바로 인접부에서의 회전 양상은 단층 방향에 따라, 즉 단층 전단성향에 따라 완전히 다른 양상을 보인다. 전단성향이 높은 단층의 경우(Fig. 2a), 단층에 접근할수록 최대주응력이 단층의 주향 방향으로 회전하는 양상을 보이는 반면, 전단성향이 낮은 단층의 경우(Fig. 2b) 단층으로 접근함에 따라 처음에는 단층 주향 방향 쪽으로 회전하다가 단층 인접 영역에서는 다시 원상복구되는 경향이 있다. 이는 전단성향이 낮은 단층의 경우 단층면상 전단변형은 낮고 단층면 수직 압축변형이 크기 때문에 국지적 최대주응력이 단층면에 수직한 방향으로 회전하는 것으로 판단된다.

Fig. 2.

Model results (orientation and magnitude of the maximum principal stress) for the four cases shown in Fig. 1. Cross-sections A-A’ are shown in Fig. 3.

불연속면 모델의 경우에는 응력 교란 양상이 상대적으로 낮게 구현되었다. 전단성향이 높은(0.58) 단층의 경우(Fig. 2c) 단층 마찰계수(0.3)가 단층 전단성향보다 매우 낮아서 주어진 응력 조건에서 미끌림이 발생하게 된다. 이 경우 최대주응력의 방향은 단층에 가까워짐에 따라 반시계 방향 회전이 발생하며, 이는 연속체 모델 결과와 정성적으로 유사하다. 단층의 전단성향이 낮은(0.35) 단층의 경우(Fig. 2d), 부여된 마찰계수 0.3보다 약간 높은 전단성향임에도 불구하고 응력 방향에 있어 교란이 거의 발생하지 않음을 확인할 수 있다.

응력의 크기는 대부분의 모델 결과에서 단층 인근에서 경계 조건으로 주어진 응력 크기(30 MPa)보다 10~15 MPa 낮아지는 경향을 확인할 수 있다. 그러나 응력이 감소 되는 영역 범위는 연속체 모델의 경우 단층을 중심으로 수 km 범위에서 발생하는가 하면, 전단성향이 낮은 불연속면 모델의 경우에는 거의 발생하지 않았다. 후자의 경우 불연속면(단층) 존재만으로는 응력 교란을 거의 모사할 수 없다.

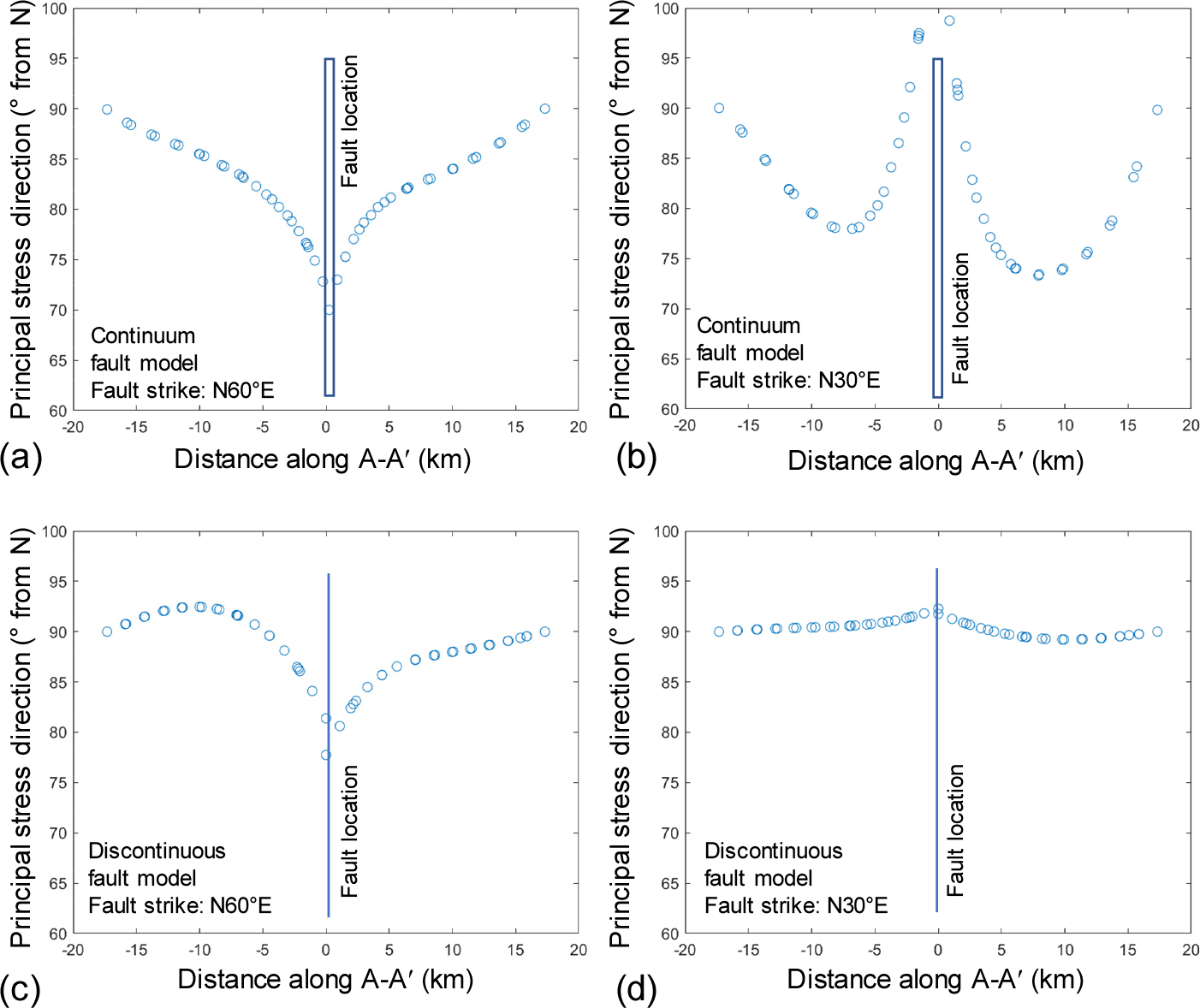
유한한 길이의 단층을 가정했기 때문에 단층 끝단에는 강한 응력집중이 발생하고 모델링된 응력 방향 또한 복잡하게 회전된다. 단층 끝단에서의 복잡한 응력 특성은 실제적인 현상일수도 있지만, 본 연구에서 이용된 단순한 단층 기하와 선형탄성의 가정에 의한 모델링 인공 산출물일 가능성이 크다. 이를 해결하기 위해 불연속면 끝단 주위에 소성영역을 가정하는 기법으로 이러한 특이성을 억제할 수 있으나 본 연구의 주목적이 아니므로 생략하였다. 이러한 단층 끝단에서의 모델링 인공 산출물 효과를 배제하고 단층 중심부에서의 효과를 정량적으로 알아보기 위하여 단층 중심에서 단층을 직교로 가르는 선(Fig. 2의 A-A’)을 따라 응력의 방향이 위치에 따라 어떻게 변화해 가는지 검토했으며 그 결과는 Fig. 3에 보이는 바와 같다. 연속체 모델에서는 모델 경계부로부터 단층에 가까워질수록 응력의 방향이 단층 주향 방향으로 회전하는 경향을 볼 수 있으나, 단층 인접 영역에서 단층의 방향에 따라 정반대의 회전 양상이 구현되기도 한다. 전단성향이 높은 단층(주향 N60°E)의 경우에는 응력의 회전 양상이 단층 위치에 이르기까지 지속해서 발생한다(Fig. 3a). 모델 경계부에서 N90°E(E-W) 방향의 최대주응력은 단층 연변에서 N70°E까지 회전된다. 그러나 전단성향이 낮은 단층(주향 N30°E)의 경우 단층으로부터 거리 약 5 km까지는 반시계 방향으로 약 15° 정도까지 회전되나 그 이후 단층으로 접근할수록 회전 방향이 오히려 역전하여 경계 조건으로 주어진 최대주응력 방향에 대해 시계방향으로 약 10° 회전되는 경향을 보인다(Fig. 3b).

불연속면 모델에서도 응력의 회전 양상은 연속체 모델의 경우와 정성적으로 유사하나 그 정도는 현격히 다르다. 전단성향이 높은 단층(주향 N60°E)의 경우 모델 경계부에서 단층으로 접근할수록 응력 방향은 반시계 방향으로 회전하며 단층 인접부에서 약 N80°E에 이른다(Fig. 3c). 그러나 전단성향이 낮은 단층(주향 N30°E)의 경우에는 전 구간에 걸쳐 2° 이내의 응력 회전이 모사되어 유의미한 수준의 응력 회전이 관찰되지 않는다(Fig. 3d).

본 연구의 목적이 두 가지 극단적인 방식으로 단층을 모사할 때 나타나는 응력 교란의 특징을 파악하는 데 목적이 있으므로 이 두 방법이 최선의 방식이라고 보기는 어렵다. 더 정교한 모델링을 위해서는 추가적인 유변학적 특성이나 물성을 각 모델에 반영하거나 두 방식을 복합하는 방법이 있을 것이다. 예를 들어 불연속면 주위에 점진적 물성 변화를 가정하는 모델을 구현한다던가, 불연속면 미끌림 거동을 조절하는 마찰계수 이외에 전단에 따른 불연속면 변형을 정의하는 전단강성(shear stiffness)을 모델에 추가하던가 하면 더 정교한 모델이 가능할 것이다. 따라서 본 연구에서 보여준 방법 중 어느 것이 최선인지를 찾는 것은 무의미할 수 있다. 그럼에도 불구하고 실제 관찰되는 현상과 비교하여 그나마 더 나은 방법을 알아가는 것은 의미 있을 것으로 판단된다.

Fig. 3.

Principal stress orientations along line A-A’ shown in Fig. 2 for the four model cases.

Fig. 4는 한반도 남동부 지역에서 수압파쇄 응력측정을 통해 규명된 최대주응력의 방향과 단층들의 분포를 보여준다(Kang et al., 2023). 대부분의 응력 자료는 양산단층과 동래단층 사이의 시추공에서 측정되었다. 이 지역에서 발생한 지진 단층면해 자료 역산을 통해 구한 광역적 최대주응력 방향은 N70°E로 규명되었으며 응력의 상대 크기를 나타내는 R값을 이용해 유추한 최소주응력과 최대주응력의 비율은 약 3으로 유추되었다(Soh et al., 2018). 따라서 앞의 수치모델의 경계 조건 응력은 이 지역의 응력 상태와 일관되게 설정되었다. 총 25개의 수압파쇄 자료 중 70%인 17개 자료가 광역적 최대 압축응력 방향인 N70°E로부터 반시계 방향으로 회전되어 있으며, 이 중 12개 자료는 반시계 방향으로 10°-40°의 범위로 회전되어 있는 양상을 보인다. 이 지역에서 양산단층과 동래단층은 모두 주어진 원거리 지구조 응력 방향과 약 60°의 각도를 보여 전단성향이 낮은 편이다. 개개의 응력측정 자료의 방향이 순전히 단층의 존재만으로 회전되었다고 보기 어려운 점도 있고, 단층에 따라 물성도 다를 수 있어서 단층의 영향에 의한 응력 회전일지라도 어느 단층의 영향으로 회전된 것인지에 관한 연구는 더 진행될 필요가 있다. 적어도 실제 측정된 응력 방향은 단층 전단성향이 낮은 경우의 불연속면 단층 모델로 모사한 결과(Fig. 3d) 보다는 지구조 응력 방향으로부터 훨씬 많이 회전되어 있음을 알 수 있다. 또한 응력 측정 위치는 단층들로부터 수 km 범위에 분포하여 연속체 단층 모델로 모사한 응력 교란 영역 범위에 분포한다고 볼 수 있다.

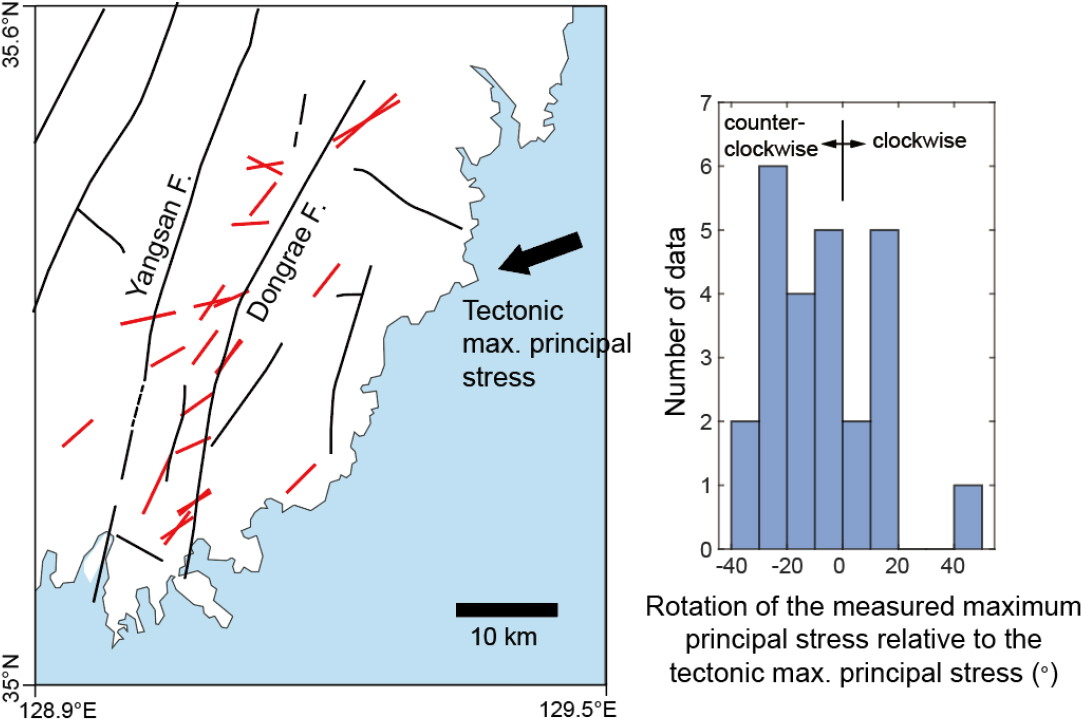
Fig. 4.

Orientations of the maximum principal stress measured from hydraulic fracturing stress measurements (red) and the distribution of faults in southeast Korea (modified from Kang et al., 2023), compared with the tectonic maximum principal stress.

균열에 의한 시추공벽 응력 교란 모델

시추공벽 응력

본 연구의 두 번째 모델은 균열이 관통하는 시추공벽에서의 응력 상태 모델이다. 원거리 응력이 작용하는 지반에 시추공을 굴착하면 시추공 주변으로 응력이 교란되면서 특정 방향으로 응력이 집중 또는 이완되는 현상이 발생하며 이는 Kirsch의 해법(식 (3))으로 잘 기술된다.

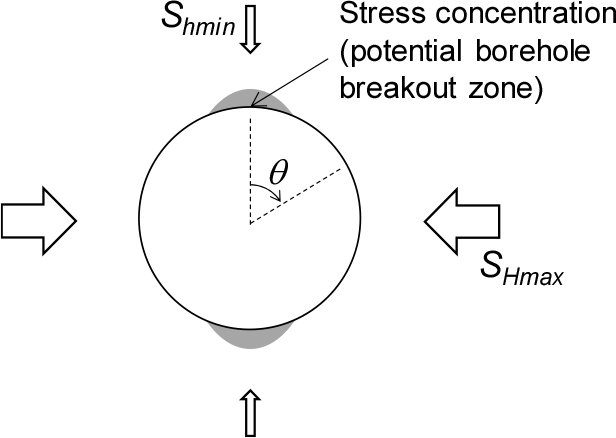
여기서, σθθ는 시추공벽 접선방향 응력, S_Hmax와 S_hmin는 원거리 최대, 최소 수평주응력, 𝜃는 S_hmin 방향으로부터의 각도이다. 시추공이 관통하는 암석이 등방, 균질하면 σθθ가 최대가 되는 방향은 항상 S_Hmax 방향으로부터 ±90°인 방위가 된다(Fig. 5). 시추공벽 응력 상태가 특히 중요한 이유는 σθθ의 크기가 암석의 강도를 초과하면 시추공벽 압축파쇄대가 발생하고 이러한 파쇄대가 항상 원거리 최대 압축응력 방향과 직교하는 방향에서 발생하게 되므로 원거리 응력 방향의 지시자로 활용되기 때문이다. 따라서 암석이 등방, 균질하면 굳이 수치분석으로 응력 상태를 구현할 필요는 없다.

Fig. 5.

Schematic showing the local stress conditions around a borehole.

그러나 시추공이 균열을 관통하는 경우에는 균열에 의한 추가 응력 교란이 발생할 수 있으므로 이 경우에 시추공벽 응력 교란은 수치분석을 이용하여야만 분석이 가능하다. 균열에 의한 시추공벽 응력 상태의 교란을 모사하기 위하여 본 연구에서는 앞의 단층 모델처럼 균열을 연속체 요소와 불연속면 요소로 각각 구현하여 결과를 비교하였다. 시추공을 가르는 균열의 3차원적 방향성을 모사하기 위하여 3차원 모델을 통해 구현하였다.

모델 설정

모델은 3 m × 3 m × 3 m의 정육면체 암체를 직경 10 cm의 시추공이 모델 상부 중심에서 하부 중심으로 관통하도록 구성하였다. 시추공은 암체 내에 평행하게 배열된 다수의 원형 형태의 균열(2 m 직경)을 관통한다(Fig. 6). 균열은 연속체 모델의 경우 폭 2 cm의 얇은 디스크 형태로 구현하였으며(Fig. 6a), 불연속면 균열의 경우에는 원형 평면 자체로 구현하였다(Fig. 6b). 균열의 방향은 추후 비교할 실자료의 경우를 참조하여 주향 210°, 경사 60°로 설정하였다. 두 모델 모두 암체는 영률 20 GPa의 선형탄성, 등방성, 균질성 매질로 가정하였다. 연속체 균열의 경우 영률 0.6 GPa, 불연속 균열의 경우 마찰계수 0.3으로 가정하여 분석하였다. 모델은 약 60,000개의 사면체 요소와 10,000개의 삼각형 요소로 격자화하였으며 격자는 시추공과 균열 주변에서 더욱 조밀하도록 구성하였다.

모델의 경계 조건 역시 추후 비교할 실자료의 경우를 참조하여 측방 한 면으로 S_Hmax 46 MPa, 직교하는 다른 측면으로 S_hmin 26 MPa, 상단면으로 연직응력(S_v) 39 MPa을 적용하였으며, 각 면의 반대쪽 면에는 롤러 경계 조건을 부여하였다. Fig. 6에 보이듯이 S_Hmax의 방향은 N70°E 방향으로 작용한다.

Fig. 6.

Models of (a) disc-shaped continuum fractures and (b) circular-shaped discontinuous fractures, traversing a borehole.

모델 결과

모델 결과는 시추공벽의 σθθ의 분포 양상에 초점을 맞추어 분석하였다. Fig. 7은 흔히 시추공 영상검층처럼 시추공벽을 360° 스캔한 후 N을 기준으로 잘라 펼쳐놓은 결과를 보여주며, 도시된 색은 σθθ의 크기를 나타낸다. 평면인 균열은 시추공벽 영상에서 사인곡선 형태로 나타난다. 이 예에서는 S_Hmax가 N70°E-S70°W의 방향으로 작용하므로 균열이 없다면 σθθ가 최대가 되는 방위각은 S_Hmax로부터 ±90°인 160°와 340°에 나타난다. 연속체 모델로 구현된 균열의 경우 최대 σθθ의 방위각이 약 30° 반시계 방향으로 회전되어 모사되었다(Fig. 7a). 반면에 불연속 균열 모델에서는 균열 바로 인접한 영역에서만 매우 국지적으로 최대 σθθ 방향이 회전될 뿐 전체적인 최대 σθθ방향은 균열이 없는 경우와 유사하게 나타난다(Fig. 7b).

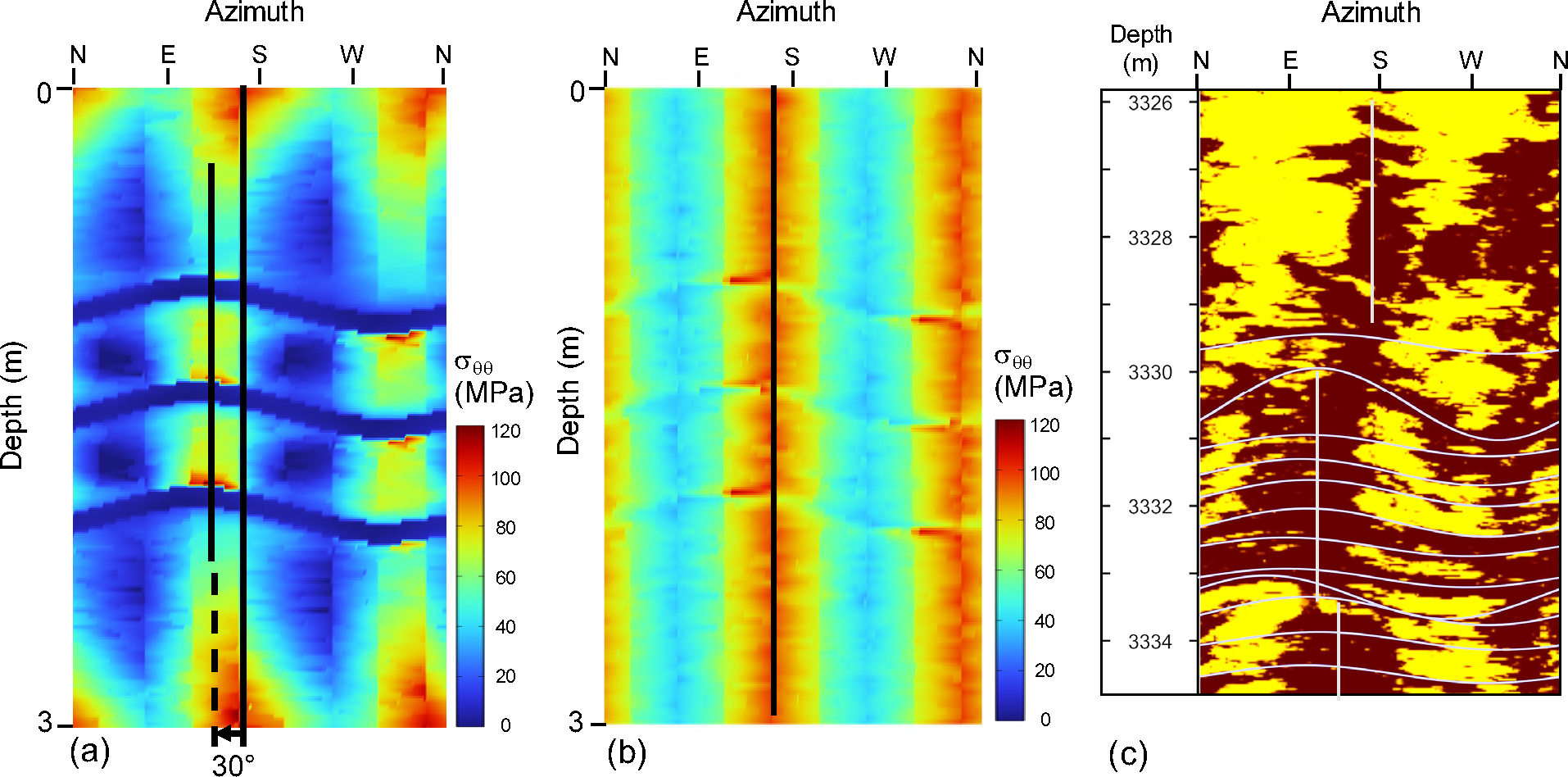
Fig. 7.

Modeled tangential stress (σθθ) patterns in a borehole wall: (a) with continuum fracture elements, (b) with discontinuous fracture planes, and (c) borehole breakouts observed in a borehole in New Zealand (from Rajabi et al., 2016).

만일 최대 σθθ 값이 해당 암석의 강도보다 높으면 암석의 파쇄가 발생하여 시추공벽 압축파쇄대가 형성된다. 사실 이 모델 예에서 사용한 균열의 방향과 응력 조건은 뉴질랜드의 타라나키 분지의 시추공에서 관찰한 사례와 유사하다(Rajabi et al., 2016; Massiot et al., 2019). 이 분지의 한 시추공에서 실제 관찰된 시추공벽 압축파쇄대는 Fig. 7c에 보인다(Rajabi et al., 2016). 이 시추공의 3,326~3,330 m 구간에는 균열이 없으며 그 하부에는 유사한 방향의 균열들이 준 평행하게 발달해 있다. 균열이 없는 구간과 있는 구간에서 발생한 시추공벽 압축파쇄대의 방위각에는 평균 약 30°의 차이가 관찰된다. 실제 관찰되는 균열의 방향에는 상당한 분산이 있어 개개의 균열에 의한 응력 교란에 대한 체계적이고 정량적인 연구가 되어야 할 것으로 생각된다. 이 현상은 연속체 균열 모델에서 균열 때문에 반시계 방향으로 회전된 σθθ의 모델 양상과 상당히 일치한다. 반면에 불연속면 균열 모델은 이러한 응력 회전 양상을 효율적으로 모사하지 못하였다.

결 론

본 연구에서는 수치모델에서 단층과 균열 등 불연속을 어떤 방식으로 구현하는 것이 불연속면에 의한 응력 교란을 모사하는 데 있어 효과적인지에 대해 두 끝 성분(연속체 모델과 불연속면 모델) 기법을 통해 검토하였다. 2차원 단층 모델의 경우, 연속체 모델로 모사한 응력 교란의 영역적 범위와 응력 회전 정도가 실제 측정한 대규모 단층 주변 응력 회전 양상과 더 유사한 것으로 보인다. 반면 불연속면 모델의 경우 응력 회전 정도와 응력 교란 영역 범위가 실제 측정한 사례보다 덜 효과적으로 모사되는 것으로 나타난다. 균열에 의한 시추공벽 응력 교란 모델의 경우에도 실제 관찰한 응력 교란 양상은 불연속면 모델보다 연속체 모델에서 더욱 효과적으로 모사됨을 확인하였다.

다시 한 번 부연하면 연속체 모델이 불연속면 주변 응력 교란을 좀 더 효과적으로 모사할 수 있다고 하더라도, 이 기법이 불연속면 모델 방식 보다 모든 면에서 우월하다고 볼 수는 없다. 불연속면 모델 방식은 단층과 균열의 취성 전단거동을 해석하는데 물리적 기반이 강고하여 전단에 동반된 균열 전파나 신장 등의 동적 거동 이해에 유리하다. 실제 수압파쇄 균열 전파 등의 연구에서는 불연속면 모델이 광범위하게 활용되고 있다(Jiang et al., 2015). 본 연구에서 검토한 단층/균열에 의한 정적 응력 교란은 매질의 불균질성을 강조하여 모사하는 것이 효과적임을 시사한다.