서 론
지하수함양은 매우 복잡한 과정 속에 강우의 빈도, 강도, 지속시간 뿐만 아니라 온도, 습도, 풍속과 지하수위 상부에 존재하는 토양 및 암반층의 특성과 깊이, 지형과 식생 분포 및 토지이용과도 관련하여 시공간적으로 매우 광범위하고 다양하게 나타난다(Memon, 1995; Healy, 2010). 따라서 지하수함양은 직접적으로 측정하기 어렵기 때문에 지하수유동 모델을 사용하여 추정하고 있다(Healy, 2010). 근래에 전 세계적으로 기후변화로 인한 이상 고온 현상과 더불어 4대강 주변에 증설된 댐, 보에 의한 하천의 수온상승은 녹조현상을 가속화하였다. 이러한 수질악화, 생태계 파괴 같은 환경문제의 해결을 위해 보의 수문을 개방하였지만 하천 주변 지하수위 저하는 인근에서 얕은 심도의 지하수를 사용하는 곳에서 농업용 용수공급 문제를 발생시켰다. 이를 해결하기 위한 도구로 Visual MODFLOW의 연구결과가 많이 활용되었다. 그러나 Visual MODFLOW는 복잡한 함양분포를 단순화하여 입력할 수밖에 없는 한계로 인해 지표수 유출 모사의 불확실성, 과도한 하도 유출 문제 등을 내포하고 있다. 이를 개선하기 위해 국내외적으로 지하수와 지표수를 연계하여 구동할 수 있는 수치모형(SWAT-MODFLOW, HydroGeoSphere, GSFLOW) 등이 개발되었지만 다양한 수문학적 입력변수를 다루는데 있어서 사용이 용이치 않아 수리지질 연구보다는 수문학 혹은 수공학적인 연구에 의해 주도적으로 사용되고 있다(Sophocleous et al., 1999; Kim et al., 2008; Markstrom et al., 2008; Sudicky et al., 2008). 따라서 다양한 수문학적 변수들을 다루는데 있어서 최근에 기후-토양-식생분포를 추정하는 연구에서 활발히 활용되고 있는 Landsat-8 위성영상으로 지하수함양량을 추정하는 연구를 수행하였다(Park and Jeong, 2020).
일반적으로 함양은 식생화된 토지피복, 관개, 토지경작, 농경지 재배작물의 위조점(wilting point), 뿌리심도 등에 의해 변화한다(Scanlon et al., 2005). 따라서 다양한 함양 인자들을 반영하여 지하수함양량을 산정하기 위해 수치모델링을 적용한 연구가 수행되었다(Tsutsumi et al., 2004; Chung et al., 2007). 이러한 결과를 바탕으로 토지이용별 지표유출량, 거주지역과 산림지역의 지하수위를 비교하여 지하수함양모델에서 토지이용변화에 대한 영향을 조사하였고(Jinno et al., 2009), 제주도의 천미천 유역에서 한국형 유역수문모형 SWAT-K(soil and water assessment tool-Korea)를 사용하여 식생에 의한 차단(interception)효과를 규명하였다(Chung et al., 2015). 전 세계 715개 지점에서 수행된 지하수함양모델에 대해 입력변수별 단계적인 평가를 통해 강우와 잠재증발산 그리고 토지이용과 토지피복인자가 가장 의미있는 인자임을 밝혔다(Mohan et al., 2018). 터키에서는 격자기반 물수지 모델인 mGROWA을 사용하여 Ergene강 유역 지하수함양의 공간적 분포에 대한 주요 영향인자는 식생, 토양 유형, 기후등으로 제시하였다(Rukundo and Dogan, 2019).
특히 토지이용, 토지피복과 함께 지하수함양인자 중의 하나인 토양 특성분포에 대한 연구는 최근 50년 동안 원격탐사분야에서 활발히 수행되었다(Sonmez and Slater, 2016). 식생에 대한 모니터링에 대해 ERTS MSS 위성영상의 밴드 5와 밴드 7의 차이가 녹색생물유기체(green bio mass)에 민감하게 반응하는 것을 발견하고 밴드 5와 7의 합을 그 차이로 나눈 매개변수를 제시하였다(Rouse et al., 1973). 식생관련 지수에 대해 경험식과의 상관성을 정리하고 실제와 가상의 예시를 통해 유용성을 증명하였고(Perry and Lautenschlager, 1984), 원격탐사의 식생-토양관계식 개념은 토양 유형을 구분할 수 있는 만큼 토양의 광학적인 특성을 잘 대변한다고 하였다(Baret et al., 1993). 실제 실험실에서 확인한 토양의 분광자료와 위성영상자료와의 상관성은 결정계수 0.9로 매우 잘 맞는 것으로 나타났다(Demattẻ et al., 2009). 인도에서는 지하수함양에서 강우와 식생 밀도의 영향을 확인하기 위해 Modis 위성영상에서 정규화된 식생지수(NDVI)를 산정하고 지하수함양량과 강우, 지하수함양량과 NDVI 상관성은 결정계수 0.858의 회귀곡선식을 따른다고 하였다(Singhal and Goyal, 2012).
현재 원격탐사에서 가장 많이 활용되고 있는 인공위성은 Landsat-8이다. Landsat-8은 이전의 Landsat-7 ETM+의 단점을 보완한 지상의 광학적인 이미지 스캐너(optical land imager, OLI)와 근적외선 탐지기(thermal infrared system, TIRS)를 장착하여 15일에 한번씩 동일지점에 대한 자료를 72시간이내에 제공해 주기 때문에 최근에 국내에서도 전남 장성군 황룡강 유역에서 시공간적인 식생과 토양관련 지수인 수직식생지수(PVI), 정규식생지수(NDVI), 정규경작지수(NDTI), 정규나지지수(NDRI)와 SWAT-MODFLOW의 시공간적인 함양량과의 상관성을 분석하여 위성영상을 통해 함양량 추정의 가능성을 제시하였다(Park and Jeong, 2020).
따라서 본 연구에서는 위성영상으로 지하수 함양변화를 추정하기 위해 복잡한 함양인자간 상관관계를 추정하기 위한 방안으로 인공지능 기계학습법의 일종인 CART 알고리즘을 이용하여 식생과 토양관련 지수외에도 소유역별 강우(PCP), 지형고도(DEM), 지형경사(SLOP), 경사방향(ASPT) 같은 기상과 지형관련 인자들을 입력변수로 하여 시공간적인 함양분포에 대한 의사결정과정을 분석하고 계절적인 함양량 변화를 추정하였다.
연구지역 및 지하수함양량 분포
본 연구지역은 김천지역으로 낙동강 최상류에 위치하고 있으며 감천을 중심으로 유역이 형성되어 있다. 소유역별 지류 연장은 0.43~12.29 km, 지류 경사는 0.001~0.132 m/m, 너비는 3.96~82.64 m, 깊이는 0.27~2.08 m, 지류 최소표고는 29.96~288.42 m, 지류 최대표고는 38.23~836.46 m이다(Fig. 1, Table 1).
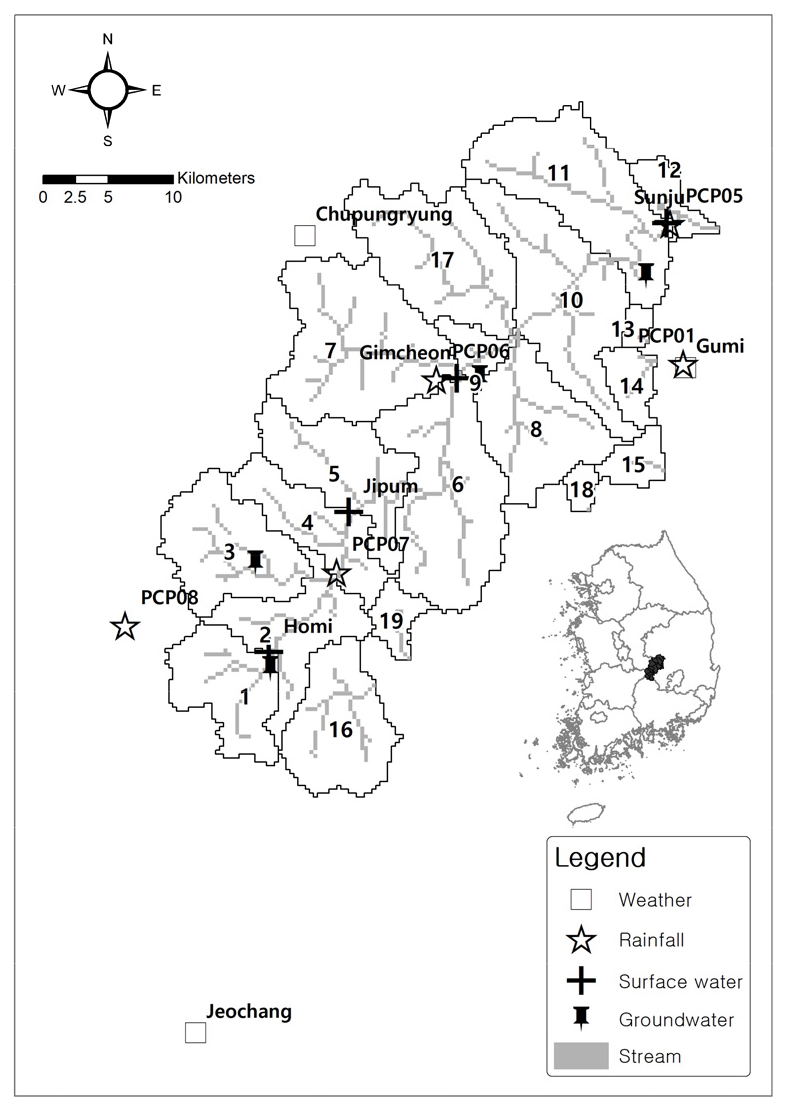
Fig. 1.
Location of monitoring point, stream, and reservoir in the subbasin including Gimcheon district (modified from MOLIT, 2016).
Table 1.
Summarized geomorphic properties of the stream according to subbasin
김천지역은 환경부와 농업과학기술원에 따르면, 16개의 토지피복/토지이용과 87개의 토양통으로 분류되며 가장 분포면적이 큰 순서대로 식생은 침엽수림, 토지이용은 논, 토양유형은 무등과 삼각 토양통이 우세하다(Table 2).
Table 2.
Classification of land use and dominant soil types
김천지역에 대한 수문성분별 모의를 위해 전체유역을 19개의 소유역으로 구분하고 각각의 소유역에 대해 토지피복과 토양도를 중첩하여 1,799개의 수문응답단위(hydrologic response unit, HRU)를 산정한 결과 FRST/SAMGAG이 가장 우세하고 다음으로 FRSE/SAMGAG순으로 나타났다(Table 3).
Table 3.
Dominant land uses, soil types, and HRU according to subbasin
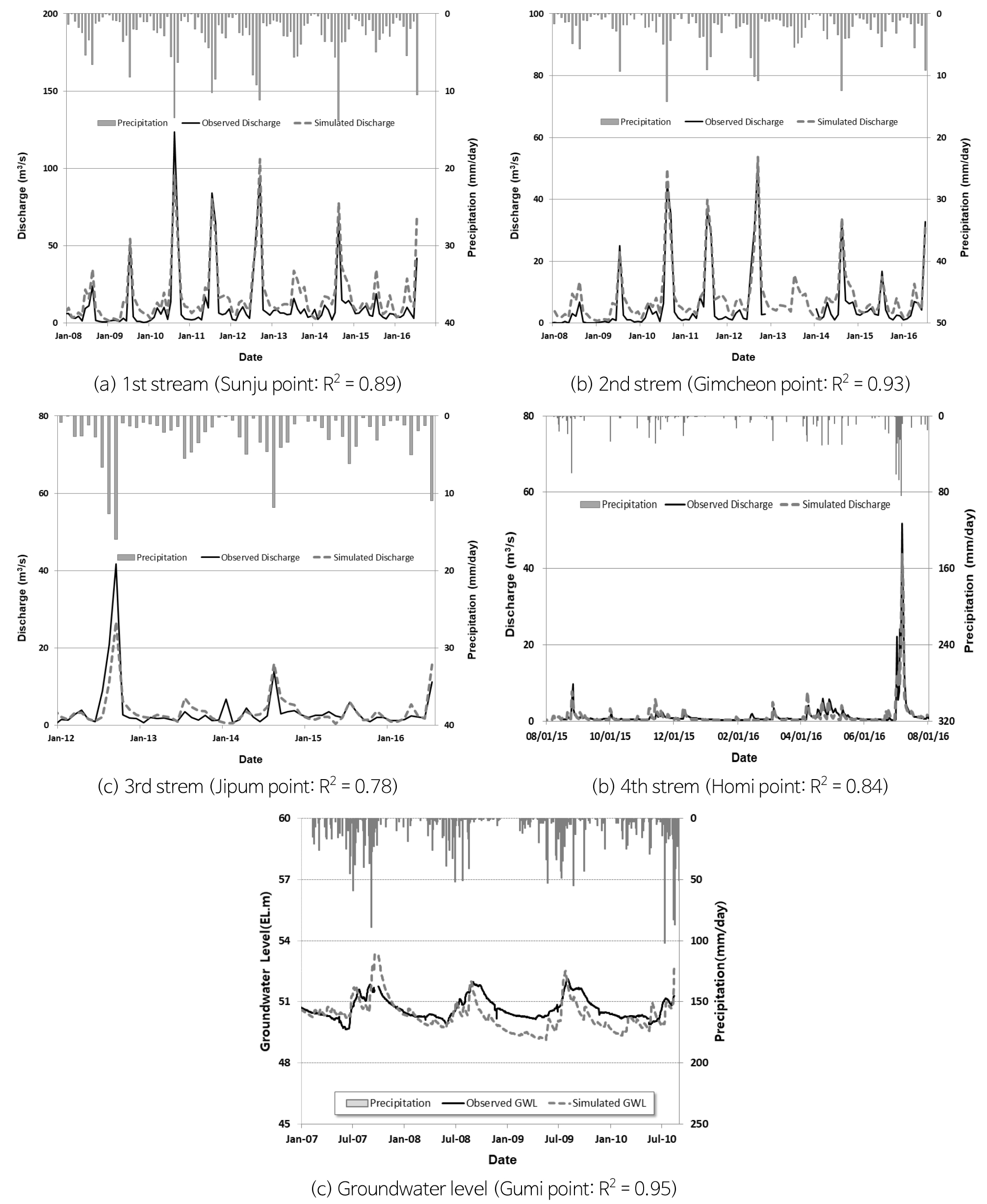
상기 지형자료를 바탕으로 수문모형을 구축하고 검 ‧ 보정을 수행하여 2004년 1월~2016년 7월까지 모의기간 중에 워밍업기간을 제외한 2008~2016년까지 수문성분을 분석하였다(Figs. 2~3, Table 4).
Table 4.
Monthly average values of hydrological components for 2008∼2015 using SWAT-MODFLOW
Note. PRECIP: total amount of precipitation falling on the HRU, ET: actual evapotranspiration from the HRU, PERC: water that percolates past the root zone, SURQ: surface runoff contribution to streamflow in the main channel, GW_Q: groundwater contribution to streamflow, LATQ: lateral flow contribution to streamflow, WYLD: abbreviation of water yield, RCH: groundwater recharge to aquifer.
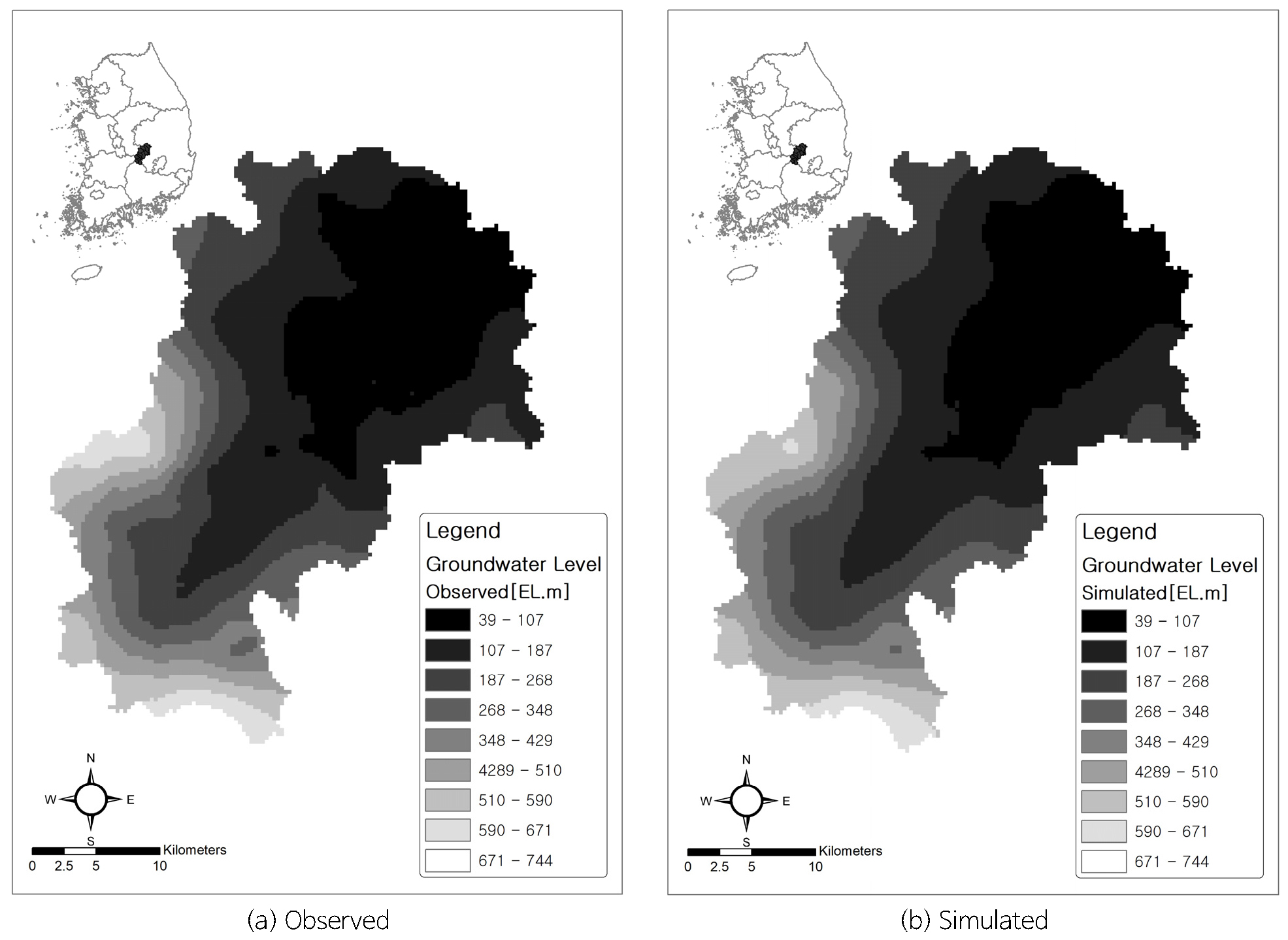
지표수유출 관측지점은 국가에서 운영하는 3개소(선주, 김천, 지품)와 지하수기초조사 당시 조사기간동안 운영했던 1개소(호미)이고 지하수 관측지점은 국가에서 운영하는 1개소(구미)이다. 지표수와 지하수 관측 시계열에 대한 모의 시계열의 결정계수값은 0.78~0.95이고, 지하수 기초조사에서 2016년 5월에 조사한 관측값의 지하수 공간분포에 대해서도 모의값에 대한 결정계수값은 0.98로서 모의값은 관측값에 대해 신뢰성이 높은 것으로 판단된다.
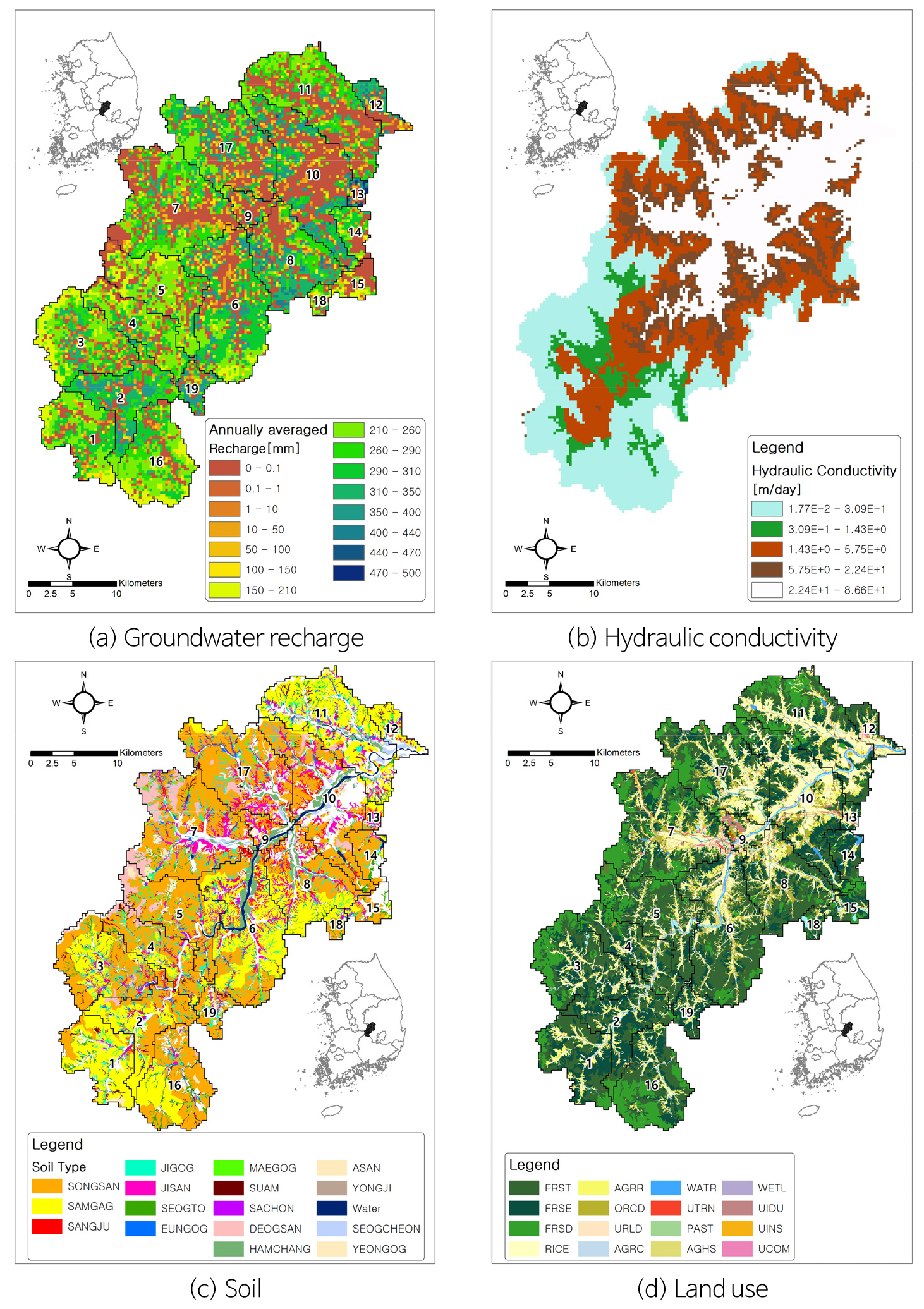
모의된 연평균 함양량에 대해 대수층의 수리전도도, 토양유형, 토지피복 분포와 비교해 보면, 함양량의 공간분포는 대수층의 수리전도도보다는 대수층 상부 토양층과 토지피복의 영향을 더 받는 것으로 나타난다(Fig. 4).
따라서 CN값이 상대적으로 높게 나타나는 덕산과 삼각 토양통이 나타는 지점에서 함양량이 작고, CN값이 작은 송산 토양통에서 함양량이 높은 것으로 나타났다. 또한 환경부 토지피복 분류상 비교적 관개가 잘 되어 있는 농경지(Agricultural Land-Row Crops, AGRR) 그리고 혼효림(Forest-mixed, FRST)혹은 침엽수림(Forest-evergreen, FRSE)지역에서 함양량이 크고, 콘크리트나 아스팔트처럼 불투수성 매질로 피복되어 있는 시가화 건조지역(UTRN, UIDU, UINS, UCOM)이나 매질의 공극률은 크더라도 분급이 나빠서 비산출률이 작은 논지역에서 함양량이 작은 것으로 추정된다.
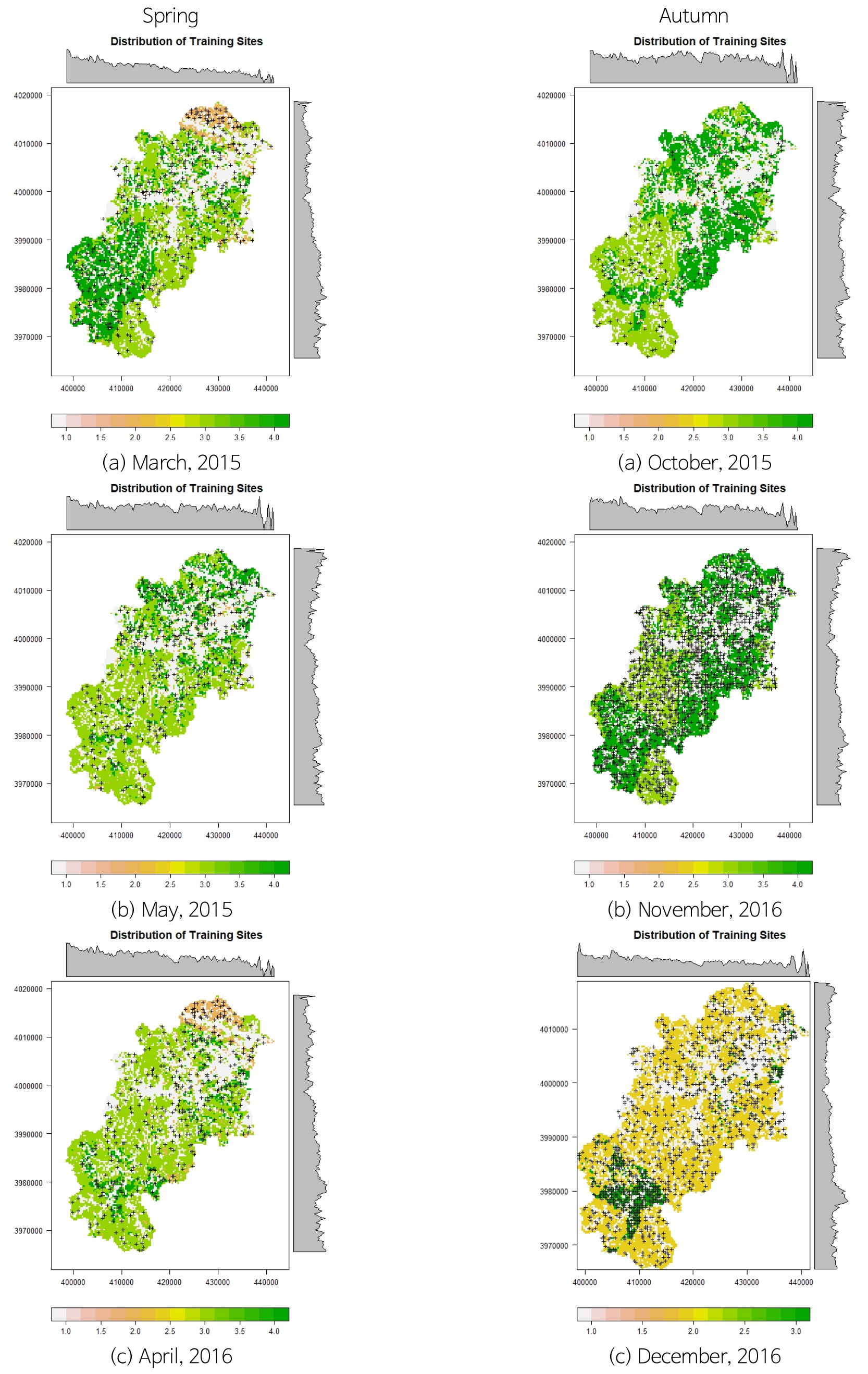
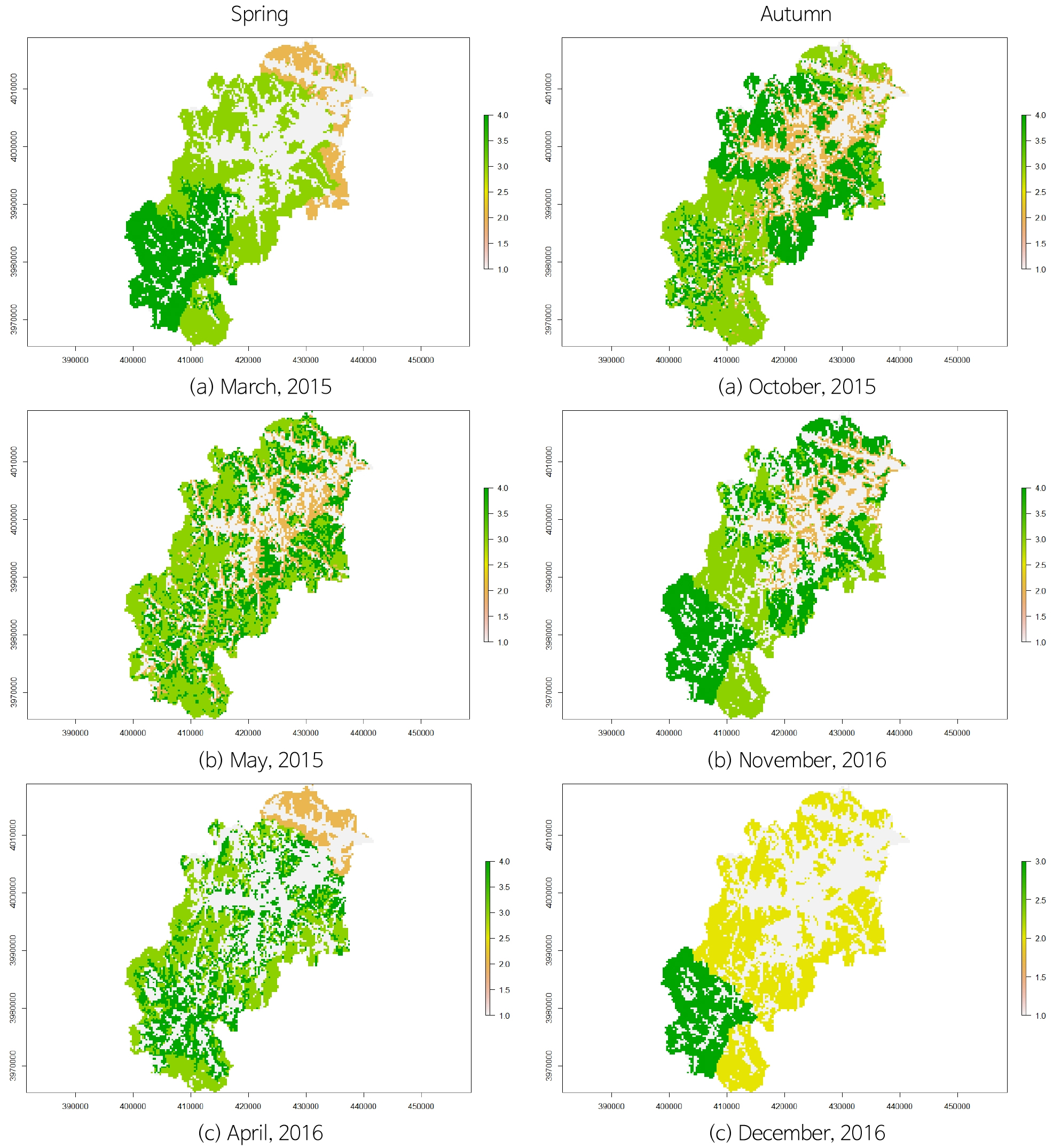
따라서 함양량의 공간적 분포는 우선적으로 지표에서 함양에 영향을 주는 토지피복 및 토양유형의 영향을 받아 불균질하게 나타나며 계절별 식생피복 및 기상인자의 변화로 인해 Fig. 5와 같이 함양량의 시간적인 분포도 변화하는 것으로 판단된다.
선행연구에 의해 함양량과 식생, 토양수분의 공간적 분포의 상관성이 확인되어 이를 통한 함양량 추정가능성을 확인하였지만 복잡한 토지이용과 토양유형을 보이는 국내현실에서 결정계수가 0.2 이하로 나타나 서로 얽혀있는 함양인자간 관계를 규명해 줄 대안이 필요한 실정이다. 본 연구에서는 이를 해결하기 위해 기계학습법의 일종인 분류회귀트리(classification and regression tree, CART)모형을 활용하여 위성영상 분석에 의한 토양-식생지수와 기상, 지형인자를 입력변수로 하여 함양량을 추정하였다.
위성영상 분석
본 연구지역에 대해 2015~2016년 조사기간 동안 분석에 사용할 위성영상으로 USGS에서 실시간으로 무료로 제공해 주는 Landsat-8 OLI/TIRS 자료를 이용하였다. 모사영역이 포함되는 촬영지점의 Path/Row는 115/035이며, 촬영일자는 조사기간 중에서 기상에 따른 제약조건 때문에 지상 상태를 가장 잘 반영하는 영상을 선택하였다. 선택한 촬영일자는 2015년 3월 23일, 2015년 5월 10일, 2015년 10월 17일, 2016년 4월 26일, 2016년 11월 20일, 2016년 12월 7일이고 위성영상 자료 분석은 USGS 사용자 매뉴얼을 참고하여 R 통계프로그램을 활용하였다(Ghosh and Hijmans, 2019; USGS, 2019).
Landsat-8의 영상에 대한 대기보정은 식생과 토지와 관련된 밴드 2~5에 대해 16비트 정수형 센서의 디지털 번호(DN)를 센서의 분광 복사휘도(spectral radiance)와 대기 상층의 반사도(top of atmosphere reflectance, TOA)로 변환하여 수행하였다.
수행된 센서의 분광 복사휘도 보정식과 대기 상층에서 반사도 보정식은 다음과 같다.
여기서, 는 분광복사휘도로서 단위는 , 은 메타파일의 밴드별 복사휘도 계수, 은 메타파일의 밴드별 복사휘도 상수, 는 디지털 번호로서 보정 전 영상의 화소값, 는 태앙각 보정 전 대기 상층에서의 분광 반사도, 는 메타파일의 밴드별 반사도 계수, 는 메타파일의 밴드별 반사도 상수, 는 태양각 보정 후 대기 상층에서의 반사도, 는 메타파일의 지역별 화면당 태양고도각, 은 메타파일의 지역별 최대 태양 고도각으로 관계에 있다.
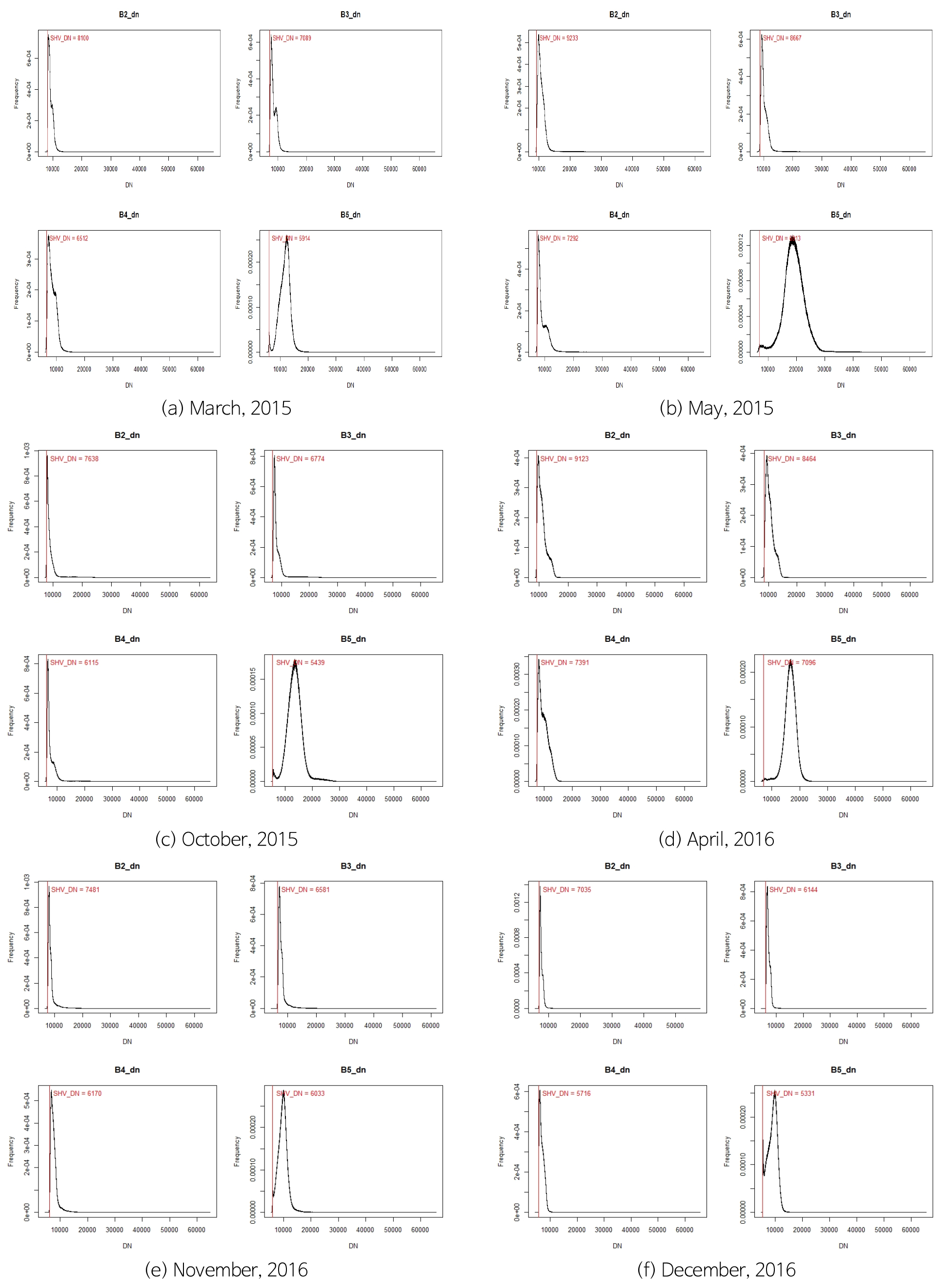
식생과 토양을 분석하기 위해서 위성영상 자료의 메타파일에서 밴드별 보정관련 정보를 활용하여 보정을 수행하였다(Fig. 6). 이를 수행하기 위해 2017년 Alexandre dos Santos가 R 프로그래밍 언어로 구축한 Landsat-8 패키지를 사용하였다(Santos, 2017). 디지털 번호를 센서에서의 분광 복사휘도와 대기 상층에서의 반사도로 변환 후 밴드별 haze 평가를 수행하였고(Goslee, 2011), 1989년 Chavez이 구축한 sodas 방법을 사용하여 대기보정을 통해 대기 상층에서의 반사값을 지표에서의 반사값으로 변환하였다(Fig. 6).
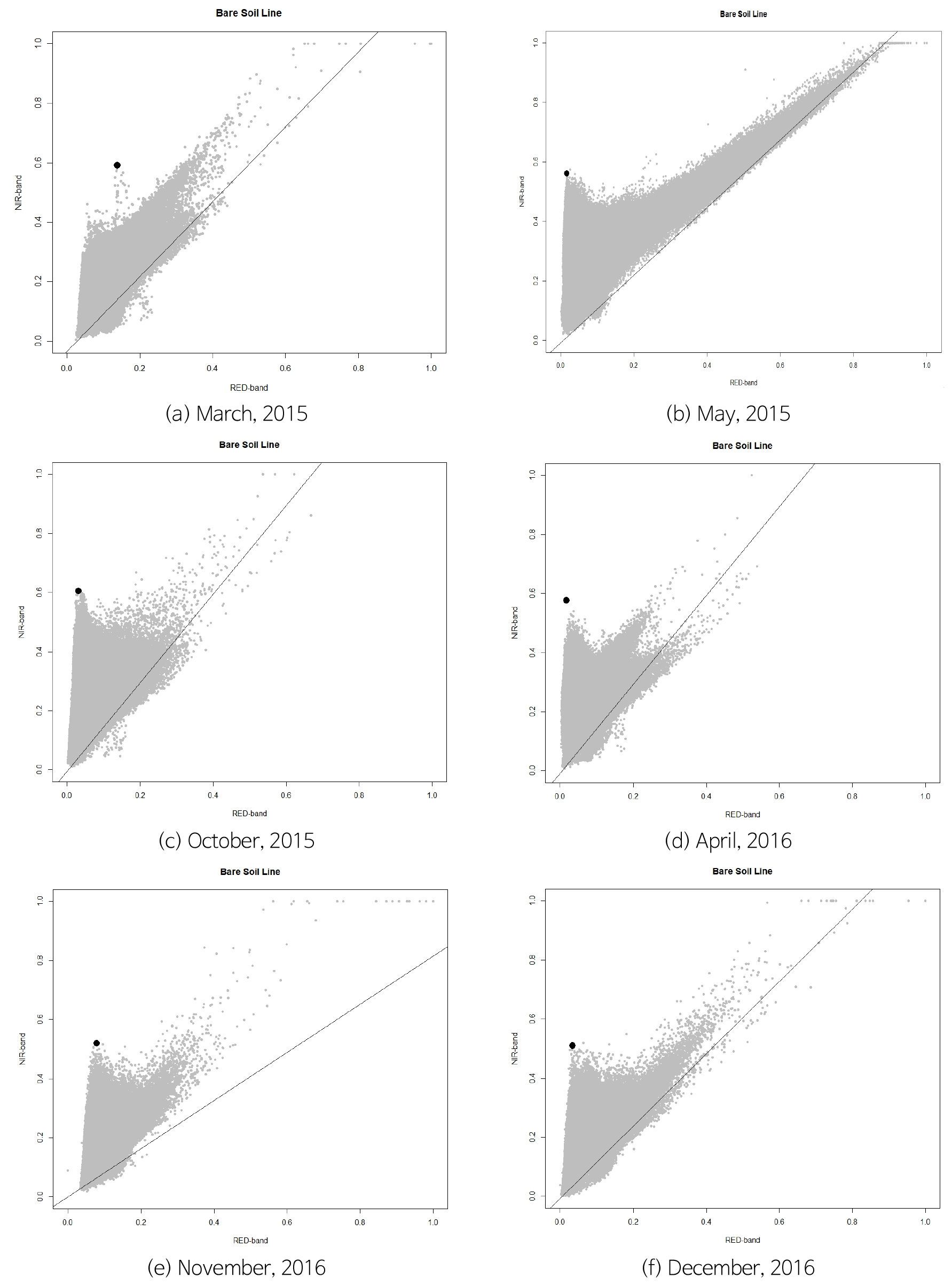
한편, 상기과정을 통해 보정된 위성영상의 밴드 4와 밴드 5를 도시하여 관측일자별 조사지역의 토양-식생 관계식(bare soil line)을 추정하였다(Fig. 7, Table 5).
Table 5.
Intercept, slope, and full canopy about bare soil line in 2015 and 2016
Red-NIR 분포에서 토양-식생관계식의 하단 전반부는 습윤한 토양상태를 반영하며 하단 후반부로 갈수록 건조한 상태를 나타낸다. 토양-식생관계식의 하단에서 상단으로 갈수록 식생밀도가 높게 나타나며 첨두점은 고밀도 식생의 캐노피를 반영한다(Koroleva et al., 2017).
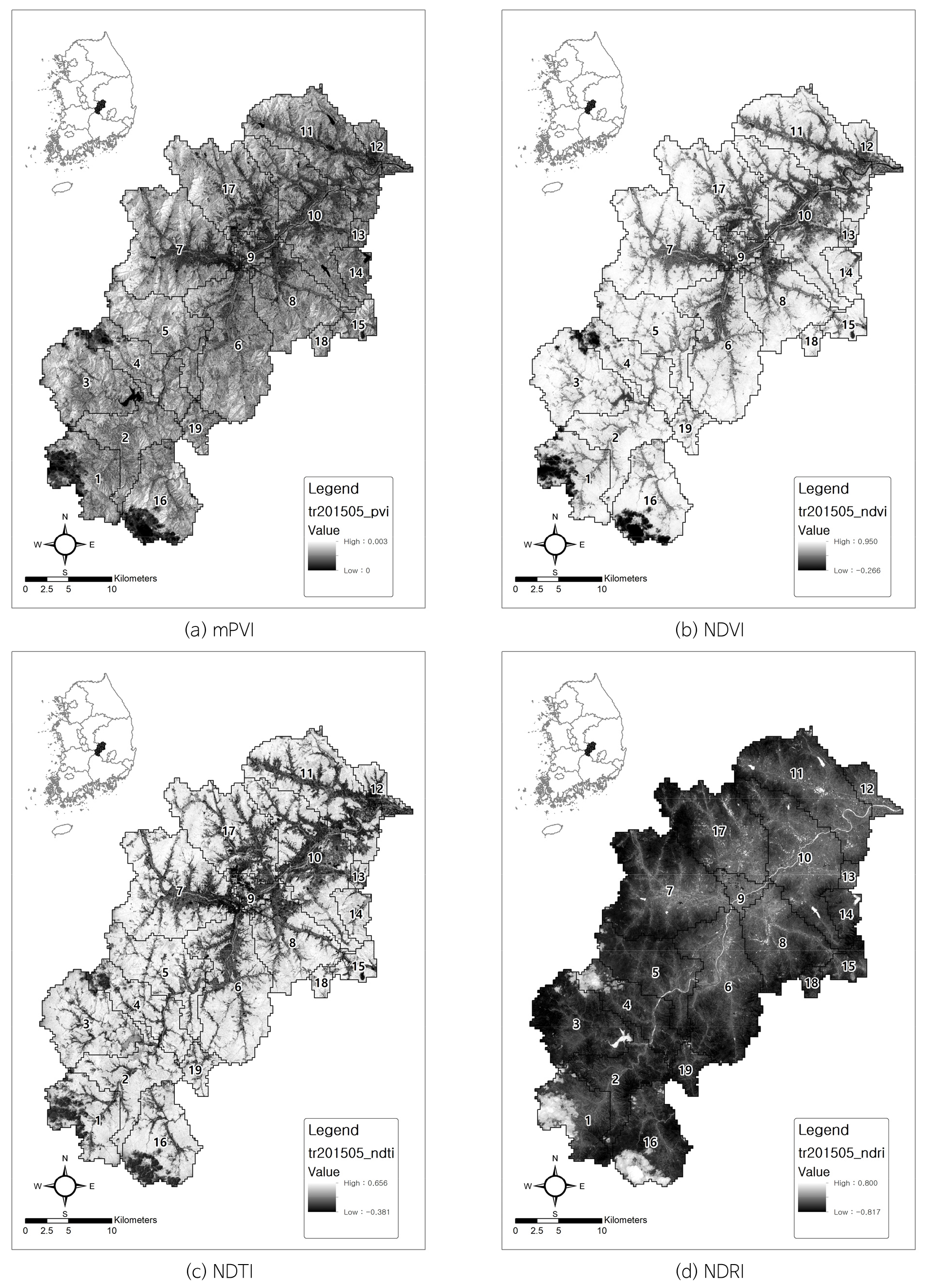
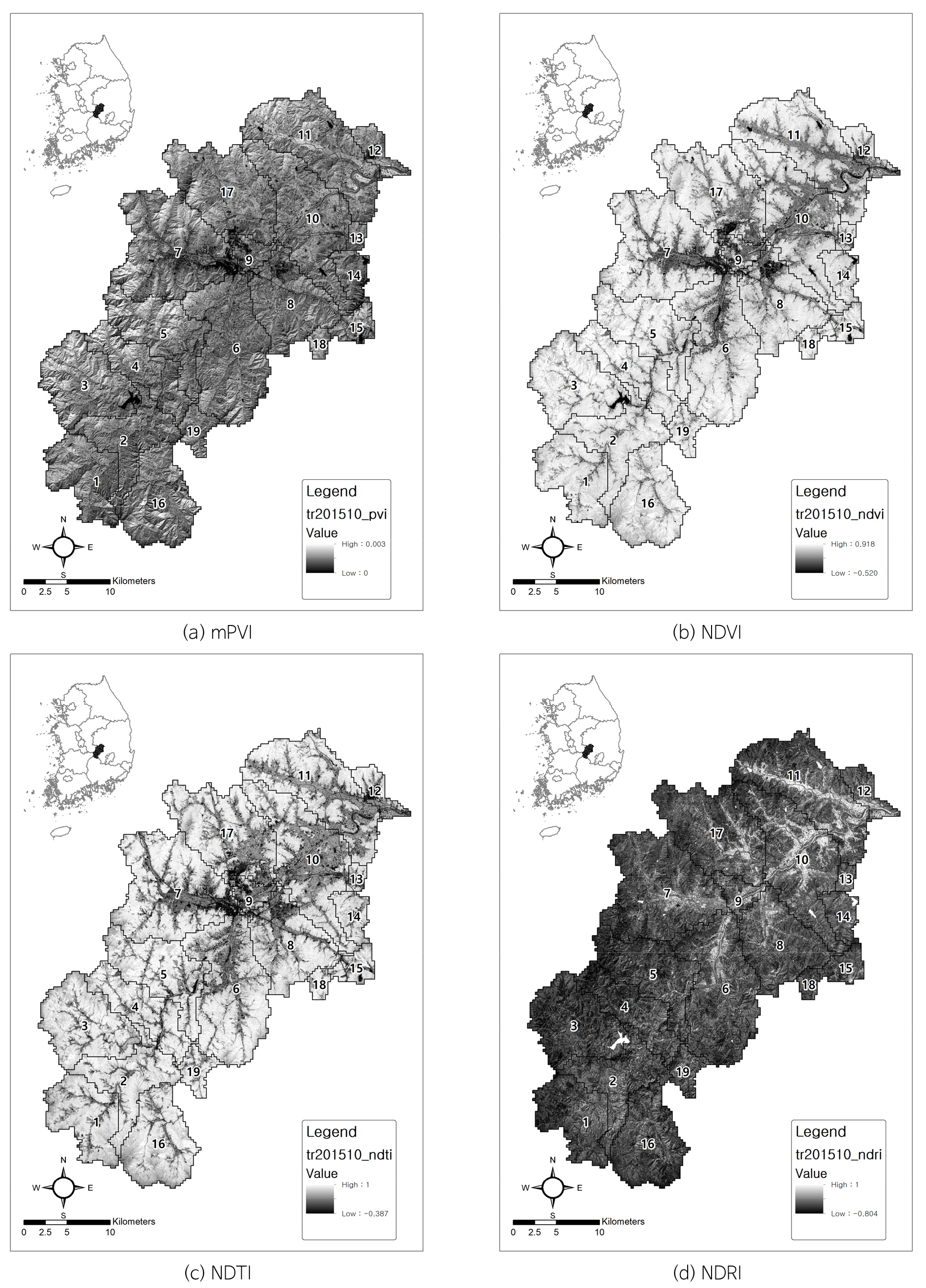
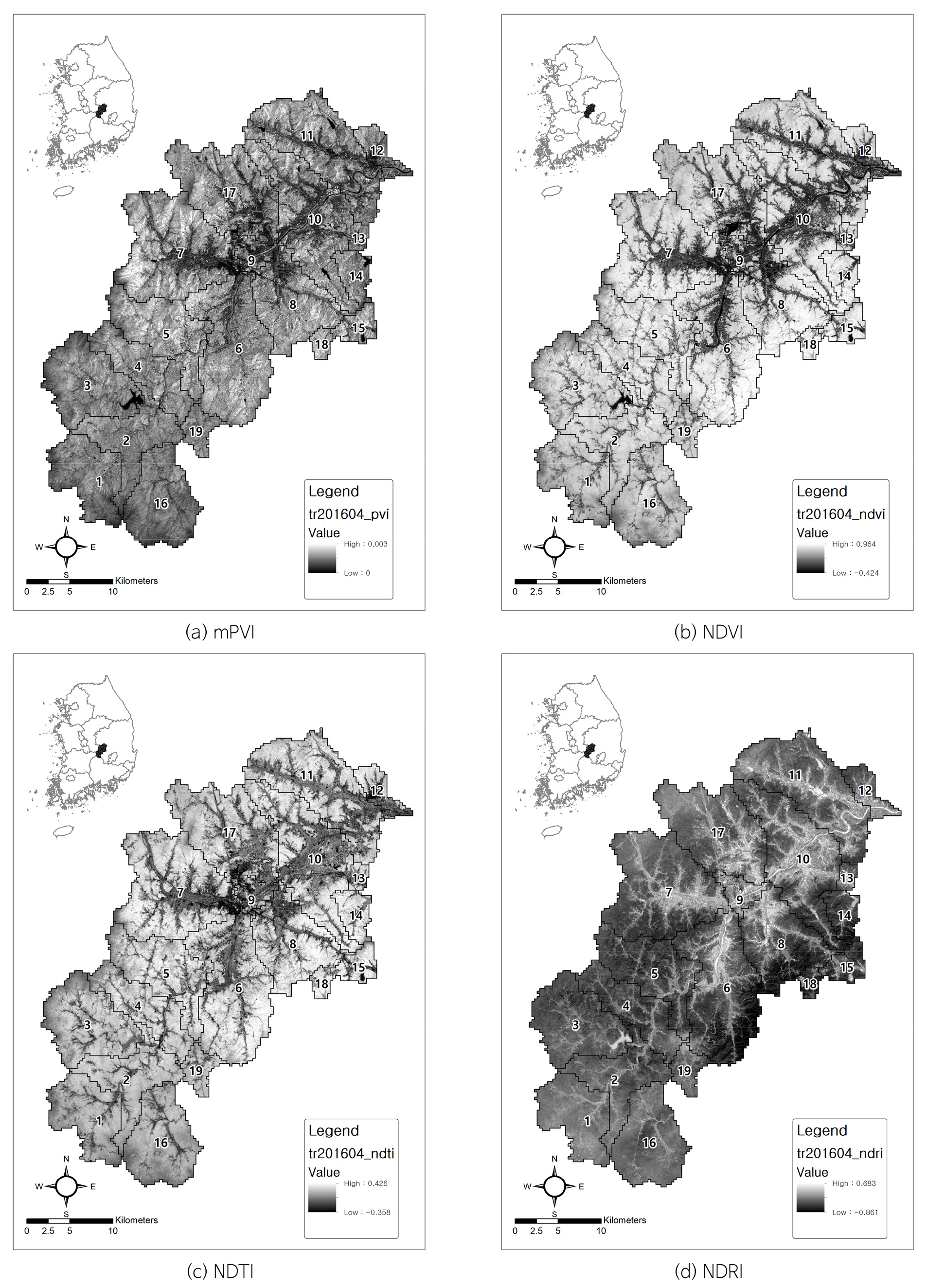
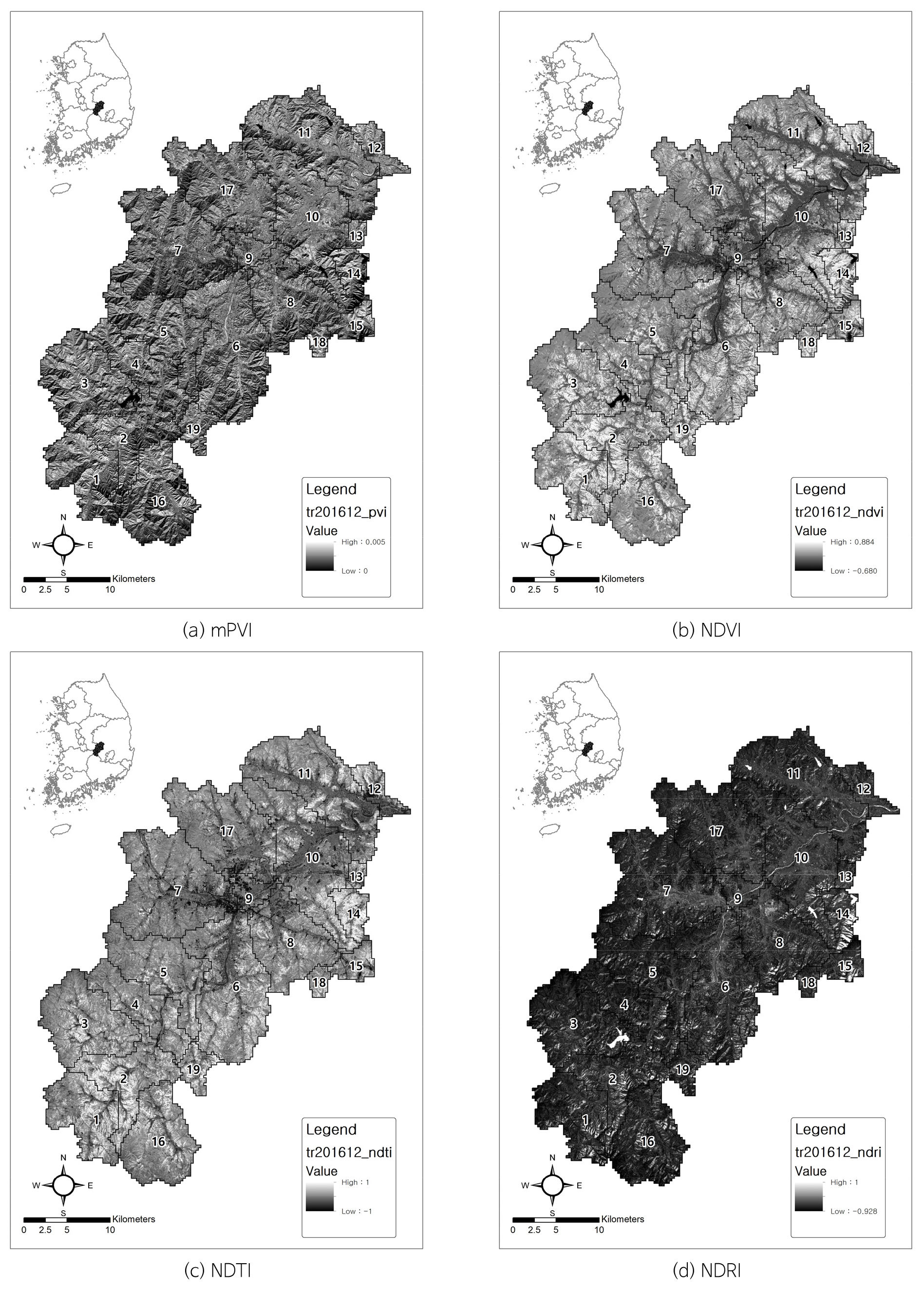
아울러 토양관계식의 기울기와 상수값을 이용하여 수직식생지수(perpendicular vegetation index, PVI)를 작성하고 선행연구결과 다른 토양-식생지수에 비해 함양량 분포와의 상관성이 낮은 것을 개선하기 위해 시행착오를 거쳐 적당한 더미상수값을 적용하였다(Park and Jeong, 2020). 그 결과 수정 수직식생지수(modified perpendicular vegetation index, mPVI)를 기존의 정규식생지수(normalized difference vegetation index, NDVI), 정규경작지수(normalized difference tillage index, NDTI), 정규나지지수(normalized difference residue index, NDRI)와 비교하였다(Table 6, Figs. 8, 9, 10, 11, 12, 13).
Table 6.
Spectral indices for vegetation, tillage, and crop residue discrimination (modified from Park and Jeong, 2020)
| Spectral index | Method of computation | Source and remarks |
|
Normalized Difference Vegetation Index (NDVI) |
for TM band (Landsat-5, but Landsat-7, Band4*1.5) from Rouse et al. (1973) | |
|
for OLI band (Landsat-8) from Burke and Dawes (2014) | ||
|
Normalized Difference Tillage Index (NDTI) |
for TM band (Landsat-5 and 7) from van Deventer et al. (1997) | |
|
for OLI band (Landsat-8) from Burke and Dawes (2014) | ||
|
Normalized Difference Residue Index (NDRI) |
for TM band (Landsat-5 and 7) modified from Serbin et al. (2009) | |
|
for OLI band (Landsat-8) from Burke and Dawes (2014) | ||
|
Modified Perpendicular Vegetation Index (mPVI) | for TM band (Landsat-5, but Landsat7, Band4×1.5) | is slope of bare soil line is intercept of bare soil line 1) if PVI < 0, then indicate water condition so, PVI = 0 2) if PVI = 0, then indicate soil 3) if PVI > 0, then indicate vegetation 4) if PVI > 1, then PVI = 1 modified from Richardson and Wiegand (1977), Perry and Lautenschlager (1984) |
for OLI band (Landsat-8) |
지하수함양량 - 위성영상 공간분포 빈도 분석
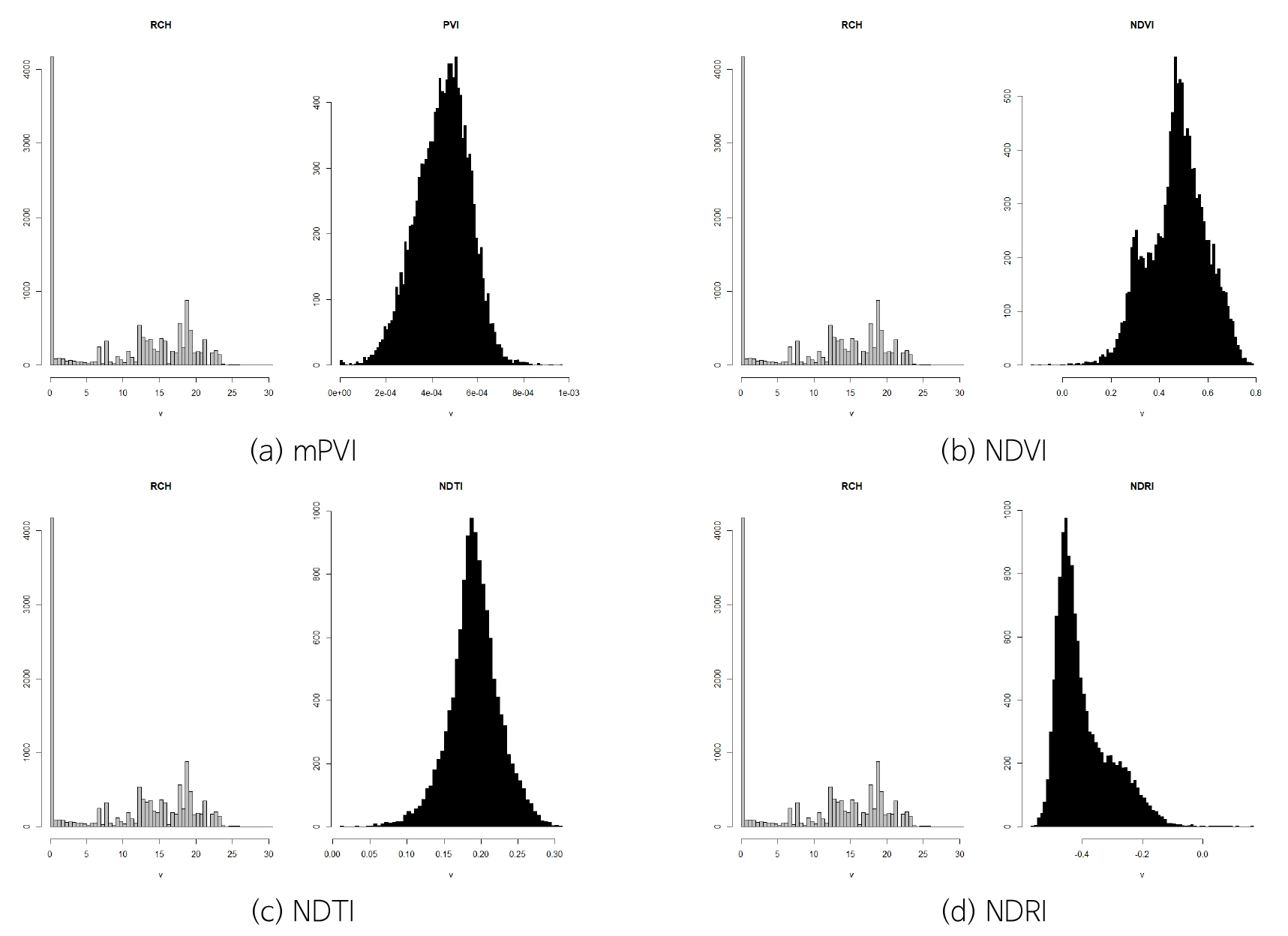
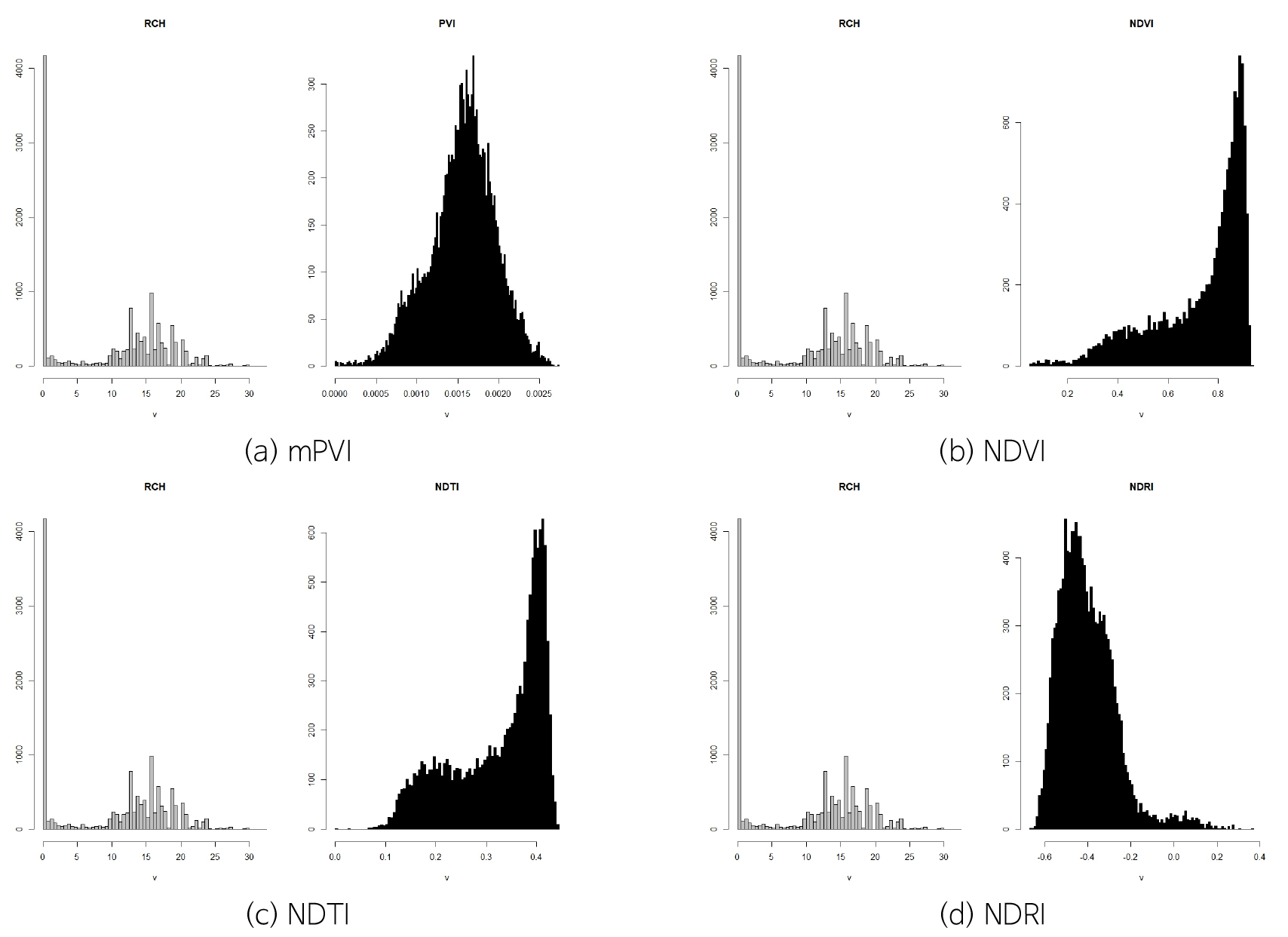
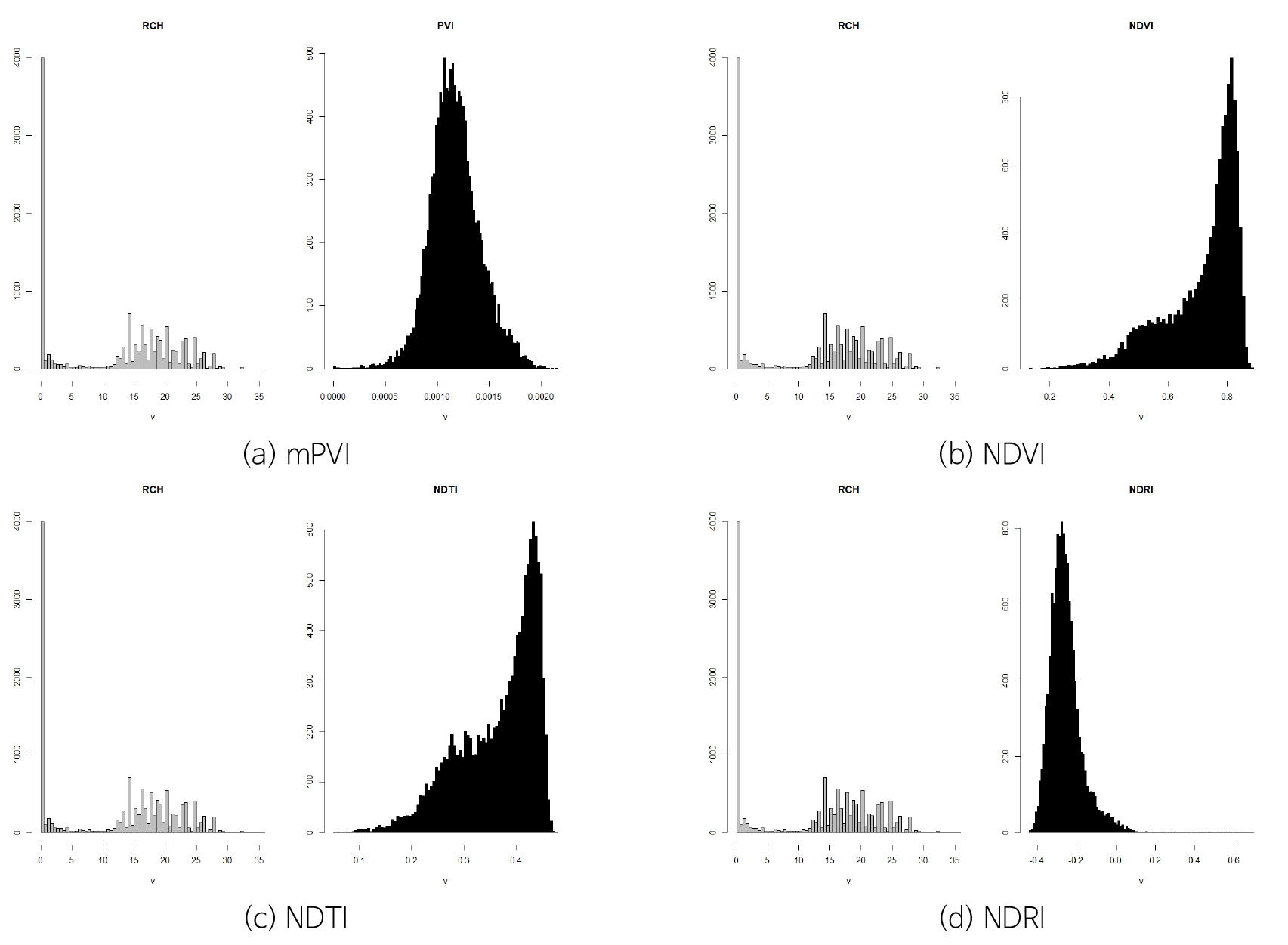
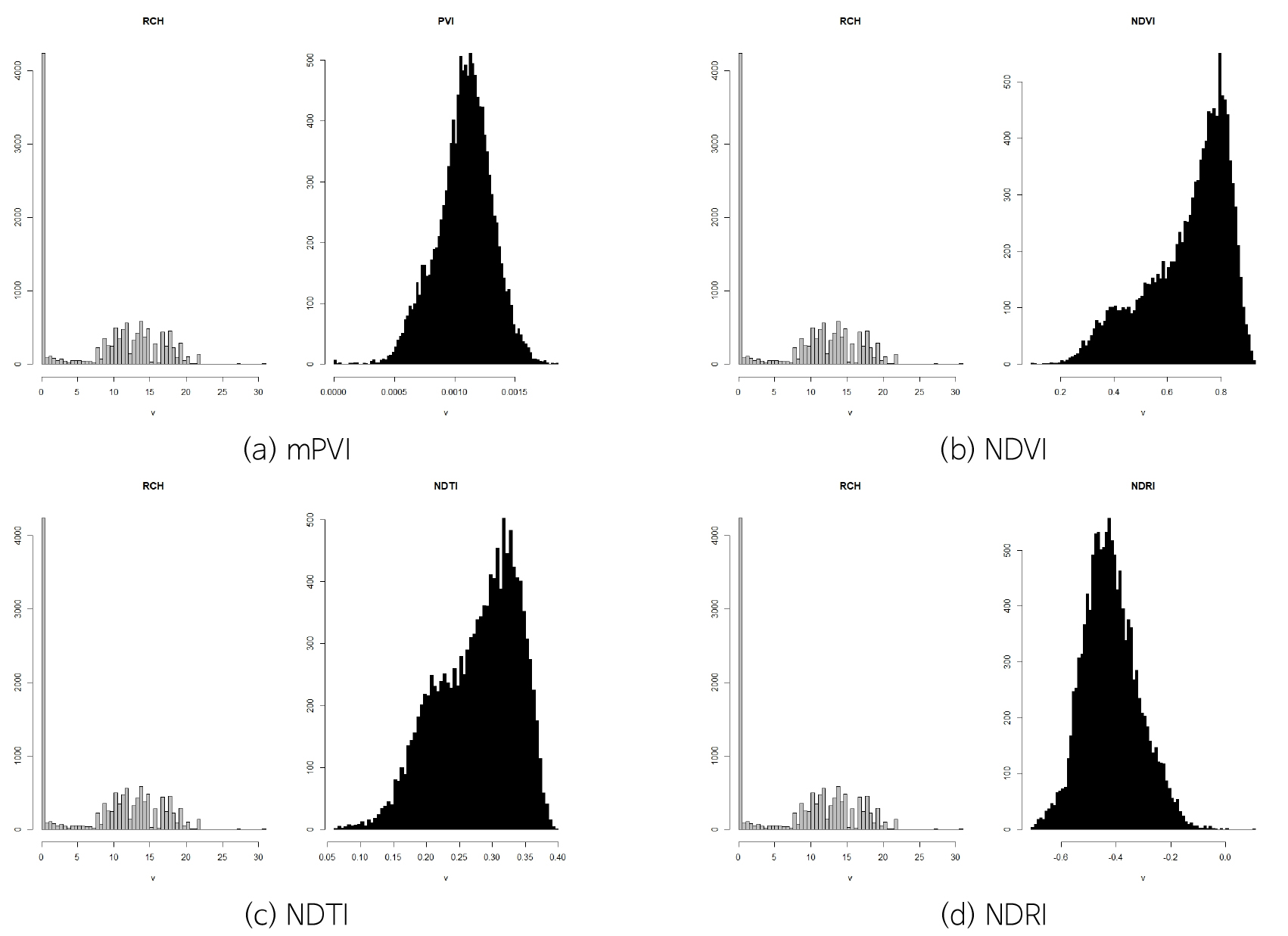
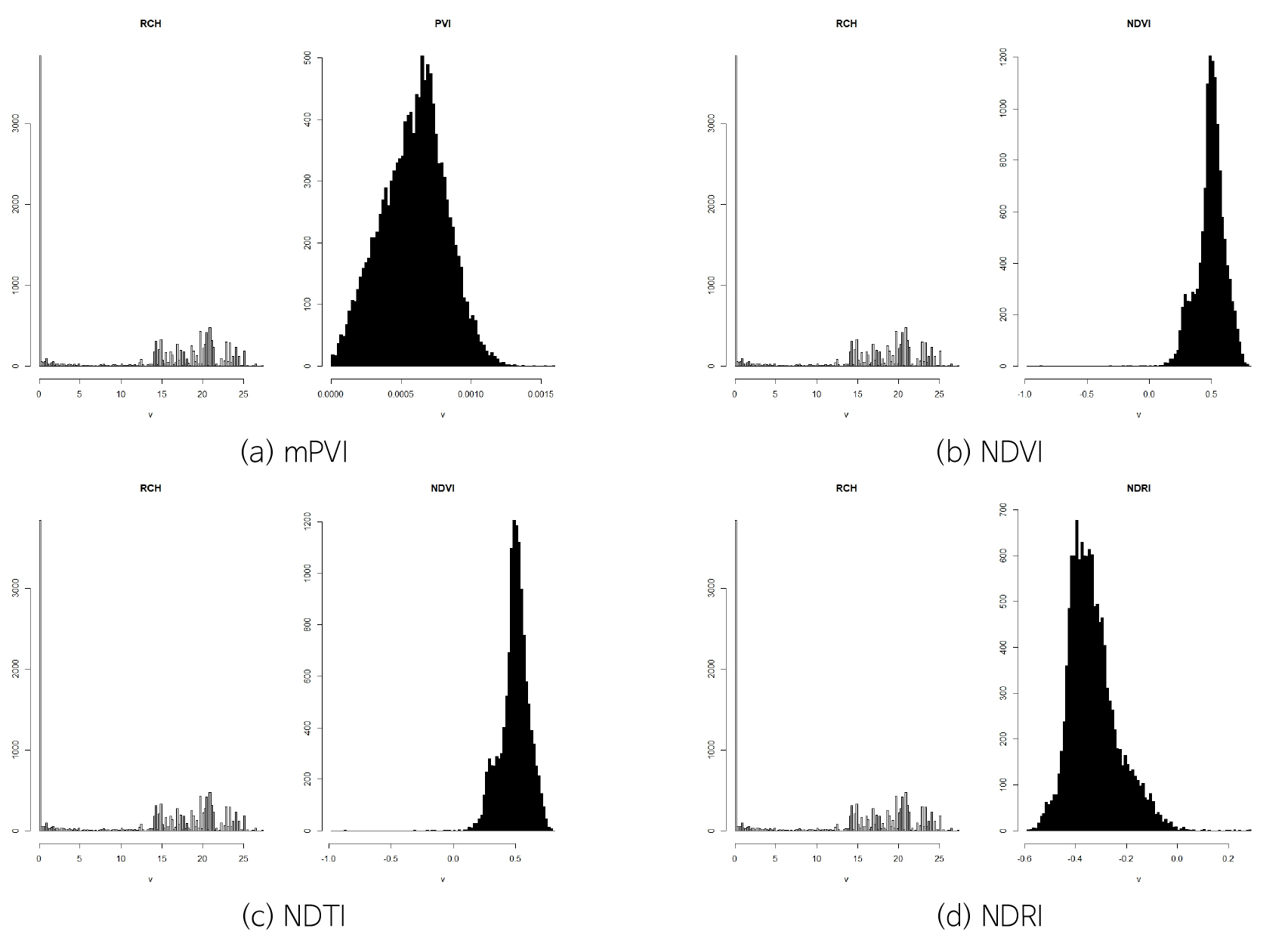
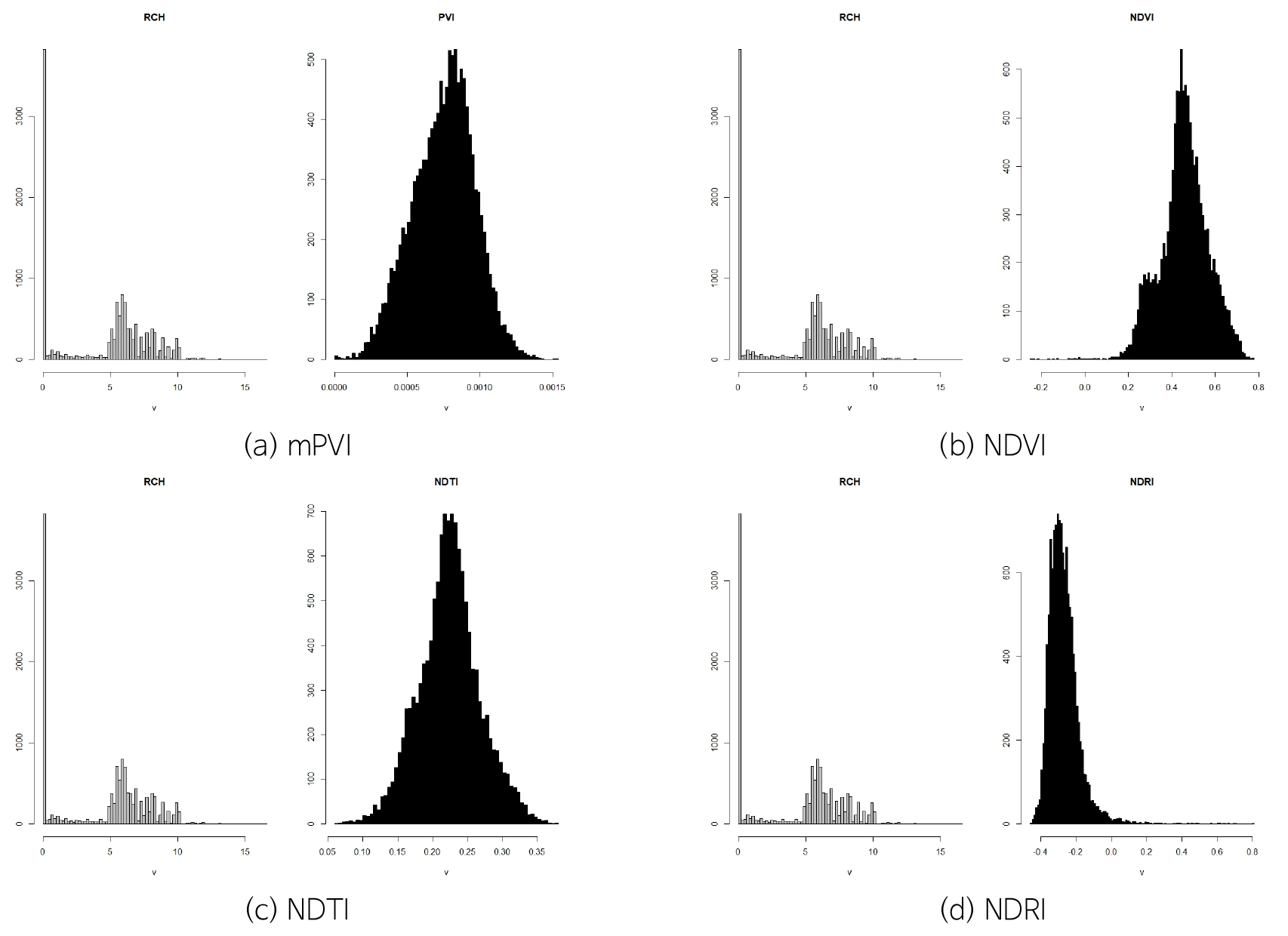
2008~2016년까지 3~5월, 10~12월 평균 지하수함양량 분포와 2015년과 2016년 해당 월의 위성영상자료를 가지고 공간분포에 따른 빈도분석을 수행하였다(Figs. 14, 15, 16, 17, 18, 19).
지하수함양량 격자와 위성영상 격자간 같은 위치에서 서로 중첩되도록 하기 위해 격자간격 300 m인 지하수 함양량에 맞도록 30 m간격의 위성영상 격자 크기를 조정하였다. 위성영상 격자크기 조정은 300 m 격자 크기 내 해당 격자의 평균값을 대표값으로 갖도록 수행하였고 이를 토대로 각 시기별 공간상의 함양량과 토양-식생관련 지수값(mPVI, NDVI, NDTI, NDRI)의 빈도분포를 비교해 보았다.
공간분포에 대한 빈도분석 결과 함양분포는 정규분포에서 벗어나는 양상인 반면, 토양과 식생상태를 반영하는 지수값(mPVI, NDVI, NDTI, NDRI)은 지수마다 일정한 분포를 나타내고 있다. 토양과 식생상태를 모두 반영한 mPVI 값들은 모든 시기에서 0~0.003 이내의 범위 내 정규분포형태를 나타내고 있으며 기존의 PVI와 함양간의 기울기보다 상대적으로 크게 나타난다. 반면, 토지경작상태를 반영한 NDTI 값들은 2015년 3월, 2016년 12월에만 mPVI와 비슷한 범위 내에서 정규분포 형태를 나타내고, 그 외 나머지 기간에는 0.5~0.8까지 첨두점의 범위가 후반부로 확대되면서 첨두점이 하나 더 나타나는 양상이다.
NDVI의 분포양상은 NDTI와 비슷한 비정규 분포이면서 두 개의 첨두점이 나타나는 경향이며 모든 시기에서 첨두점이 0.6~1사이에 분포한다. 반면에 NDRI는 -0.8~0사이에 분포하며 2016년 4월에는 -0.4를 기준으로 정규분포와 비슷한 형태를 나타내고 있다. 전체적으로 갈수기인 3월과 12월에서 NDVI, NDRI를 제외하고 정규분포형태를 나타내고 있다.
지하수함양량 - 위성영상 상관성 분석
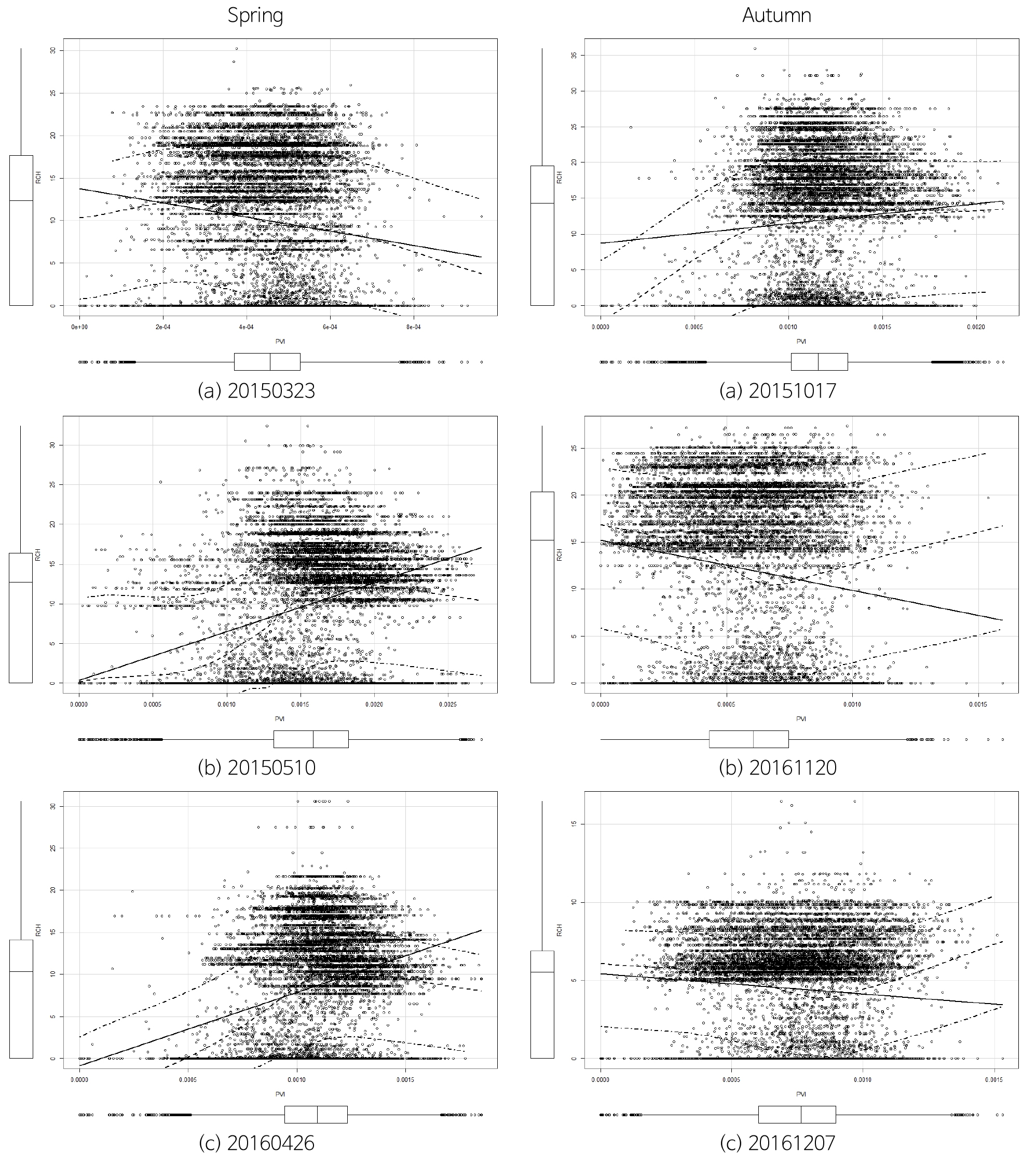
광학위성영상 특성상 구름에 의해 자료의 왜곡이 상기는 여름과 겨울을 제외하고 동일한 격자상에서 봄, 가을 계절별 지하수 함양량과 토양-식생관련 지수에 대해 전통적인 회귀분석을 수행하였다(Tables 7~8, Fig. 20).
분석결과, 상대적으로 함양량에 대해 결정계수가 큰 토양-식생관련 지수는 NDVI와 NDTI이며 산술/기하/조화 평균에서 모두 표준편차보다 1 order 크게 나타나 상대적으로 함양량과의 상관성이 큰 것으로 판단된다. 한편, NDRI는 평균보다 표준편차가 크며 mPVI는 반대로 나타나서 선행연구와 비교할 때 mPVI는 기존의 PVI가 NDRI보다 결정계수가 1 order 낮았던 것이 개선되었다.
Table 7.
Statistical summary of R-squared for correlation of distribution between results according to geomorphological/meteorological data and monthly averaged groundwater recharge using SWAT-MODFLOW by season
Table 8.
Coefficient of first-order regression equation for correlation between spectral indices and monthly averaged groundwater recharge by season
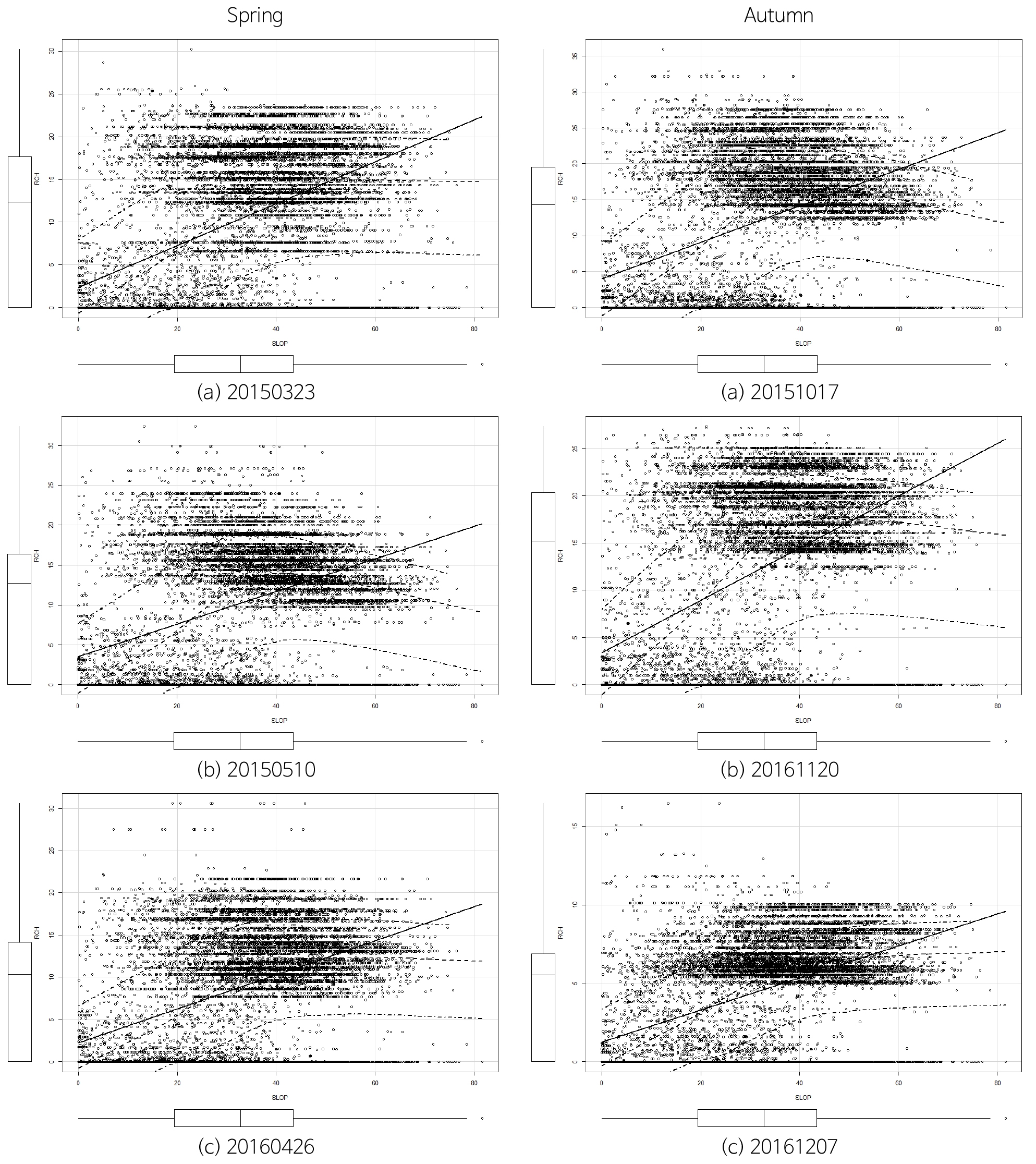
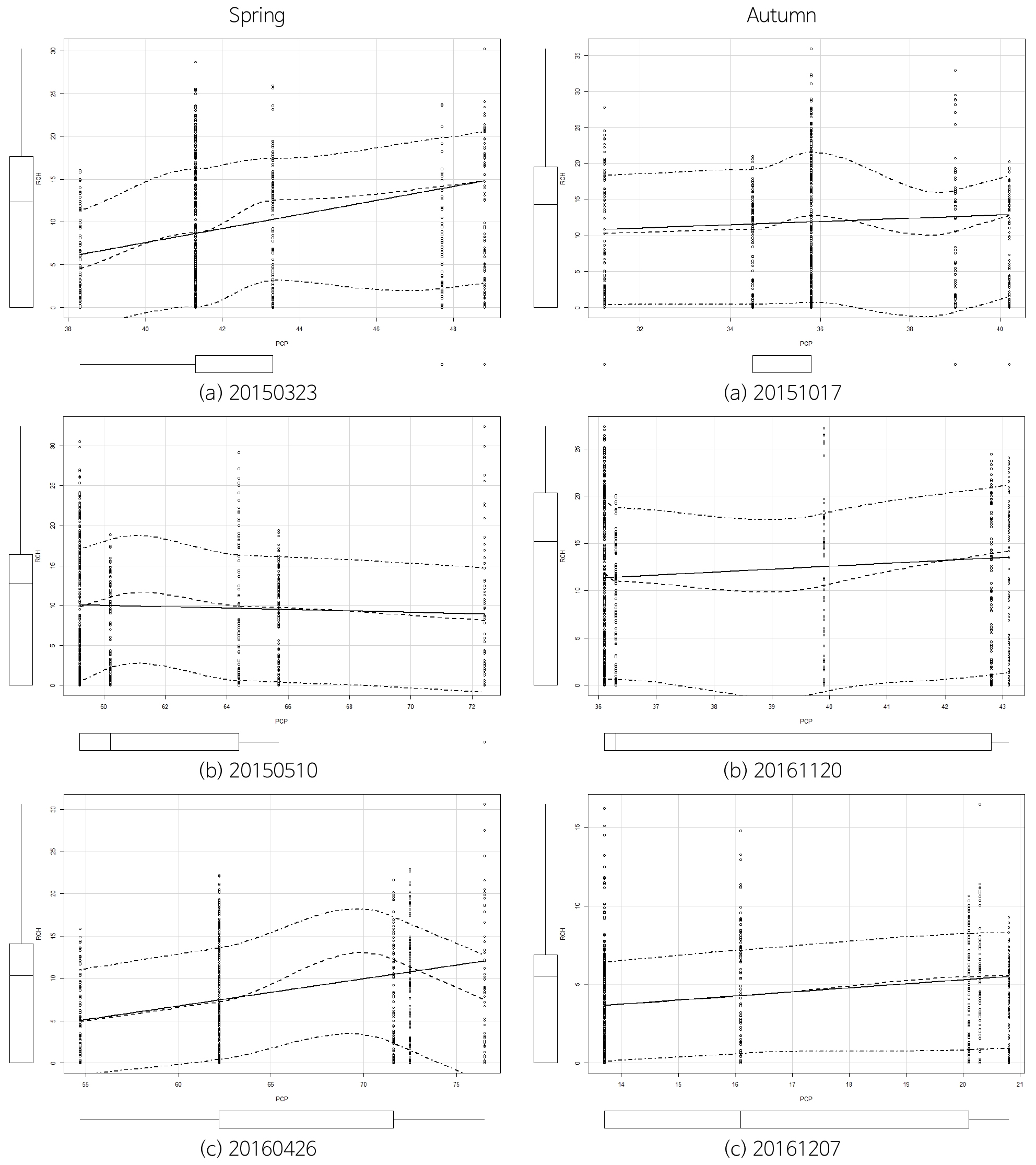
지하수함양량에 대한 식생과 토양관련 지수에 대한 회귀분석 결과, 결정계수가 최대 0.2 이상으로 나타나는 식생과 토양관련지수 이외에도 지하수함양에 주도적으로 영향을 주는 기상인자와 지형인자를 추가하여 분석해보았다(Tables 9~10, Figs. 21~22).
분석결과, 상대적으로 함양량에 대해 결정계수가 큰 기상/지형 인자는 지형경사(SLOP)이며 산술/기하/조화 평균에서 NDVI나 NDTI처럼 표준편차보다 1 order 크게 나타나 상대적으로 함양량과의 상관성이 큰 것으로 판단된다.
전반적으로 지형경사(SLOP)은 NDVI처럼 함양량과 높은 상관성을 나타내면서 좀더 정규분포를 갖고 있기 때문에 당초 예상했던 강우인자보다 더 함양과정에 영향을 주는 것으로 판단된다.
한편, 봄, 가을철 강우분포를 보면 봄철에는 4월의 강우 강도가 상대적으로 크지만 함양량과의 1차 상관식의 기울기는 3월이 큰 편이며, 풍수기에서 갈수기로 넘어가는 가을 보다는 갈수기에서 풍수기로 시작하는 봄철의 함양량과의 상관성이 큰 것으로 나타나 상대적으로 식생의 영향을 덜 받는 갈수기의 강우시 지하수로의 함양 효과가 상대적으로 큰 것으로 판단된다.
Table 9.
Statistical summary of R-squared for correlation of distribution between results according to geomorphological/meteorological data and monthly averaged groundwater recharge using SWAT-MODFLOW in the season
Table 10.
Coefficient of first-order regression equation for correlation between spectral indices and monthly averaged groundwater recharge by season
위성영상을 통한 지하수함양량 추정
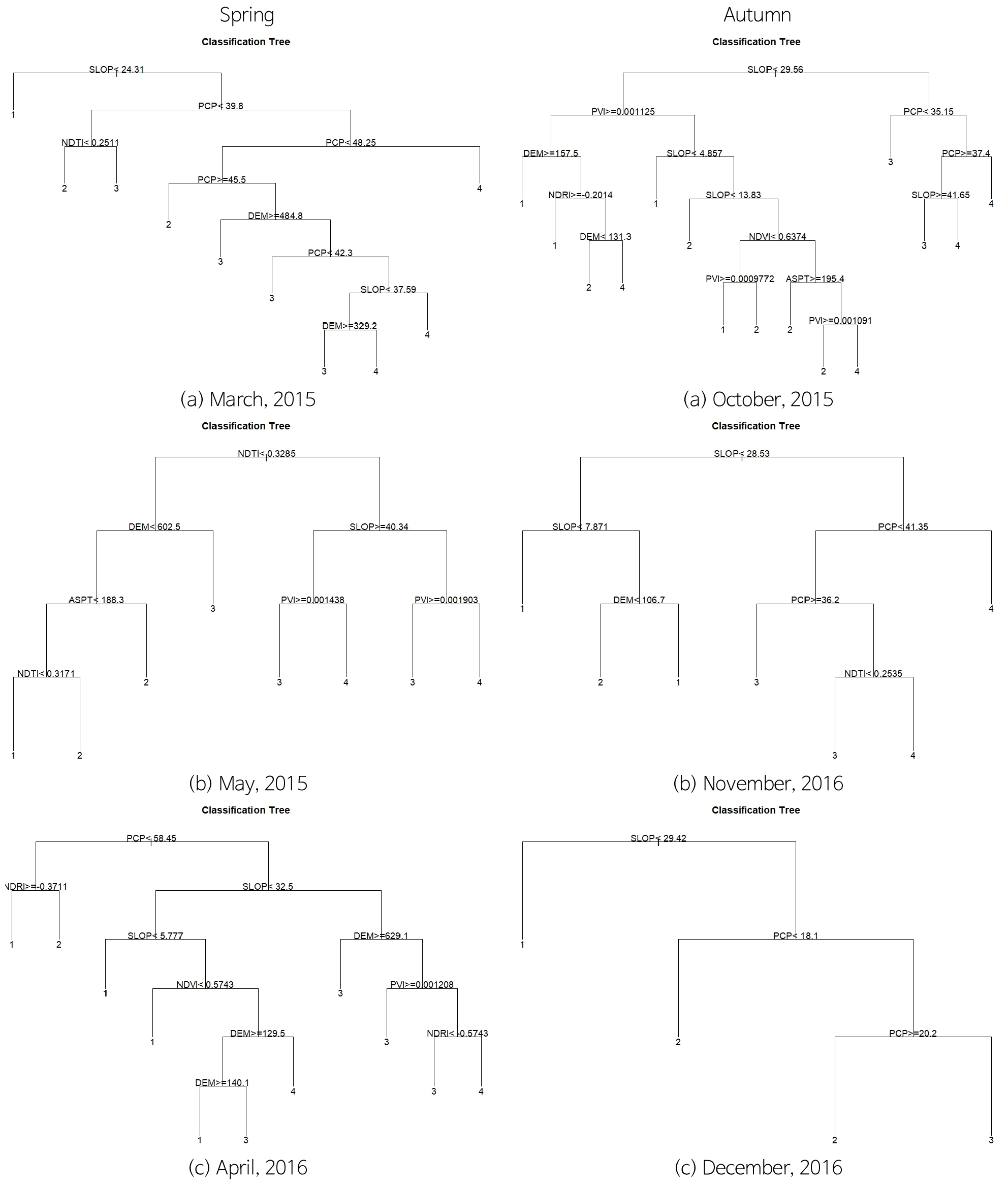
지하수함양량 추정에는 복잡한 함양인자간의 관계를 계절별 위성영상자료의 공간분포에서 CART(classification and regression tree)모형을 사용하여 함양과정에 대해 군집과 회귀방법에 의한 의사결정트리로 나타내어 지하수함양량을 추정하였다(Figs. 23, 24, 25, 26, 27, Tables 11, 12, 13, 14).
CART분석은 전통적인 통계분석과는 다른 분석기법으로 마치 나무를 심는 것(tree-building)과 흡사하며 전통적인 다변량 기법에서 불가능한 예측치간의 복잡한 상호작용을 규명할 수 있다(Breiman et al., 1984). CART 같은 분류트리모형은 판별(discriminant) 분석이나 최소자승법같이 사용자분류(user-specified) 모델에서 정상성(normality)을 가정하지 않기 때문에 반응값이나 특징적인 벡터값을 설명할 수 있는 일련의 관측치로부터 예측을 수행하기에 편리하다.
의사결정나무에 의한 단계적 과정은 나무에서 분기하거나 분기하지 않는 2개의 자식노드로 세워지며 주로 하향식 기법으로 진행된다. 각 진행단계에서는 주어진 자료집합을 가장 적합한 기준으로 분할하는 변수값이 선택된다. 분할적 합성의 기준에는 지니불순도, 분산감소 같은 것이 있는데 이 기준은 가능한 데이터 집합 분할의 경우 수마다 적용되며 그 결과 값들은 병합되어 데이터 집합의 분할이 얼마나 적합한지 측정하는데 사용된다.
지니 불순도는 집합에 이질적인 것이 얼마나 섞였는지를 측정하는 지표이며 CART 알고리즘에서 사용한다. 어떤 집합에서 한 항목을 뽑아 무작위로 라벨을 추정할 때 틀릴 확률을 말한다. 집합에 있는 항목이 모두 같다면 지니 불순도는 최소값(0)을 갖게 되며 이 집합은 완전히 순수하다고 할 수 있다.
항목의 집합에 대한 지니 불순도를 계산하기 위하여 인 를 가정하고 를 로 표시된 집합 안의 항목의 부분이라고 했을 때, 식 (4)와 같이 나타낼 수 있다.
CART에서 소개된 분산감소기법은 목표 변수가 연속적일 경우(회귀 트리)에서 자주 사용된다. 즉, 만약 다른 방법에서 분산감소기법을 사용하기 위해서는 목표 변수를 적용하기 이전에 먼저 이산화 과정을 거쳐야 함을 의미한다. 노드 N에 대한 분산감소는 노드의 분할로 인해 발생하는 목표 변수 x의 분산의 총 감소로 정의된다.
, , 를 각각 분할 전 샘플 지표의 설정이라 하고 분할 테스트가 참이거나 거짓일 때 해당하는 샘플 인텍스는 다음과 같이 나타낼 수 있다.
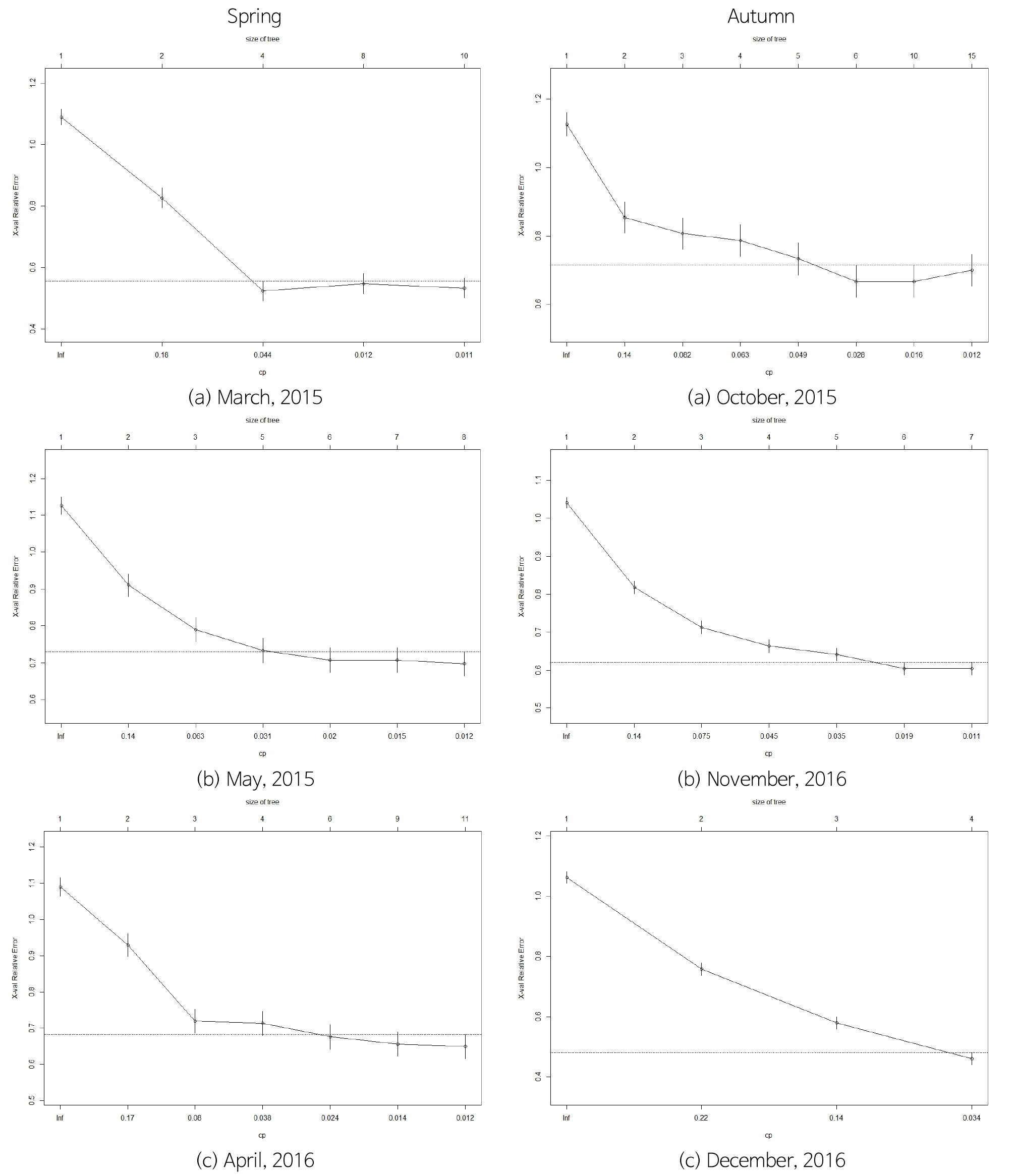
따라서 CART 분석을 수행하기 위해 Fig. 23과 같이 분산을 고려하여 SWAT-MODFLOW의 함양량 분포를 4개의 범위로 나누고, 각각의 함양범위에서 다양한 추출을 무작위적으로 시행하여 자식 노드의 분기를 최소화하면서 분기관련 CP값을 0.01에 근접하도록 추출을 시행하고 교차상관오차의 감쇠양상이 지수적으로 나타나도록 트리모형의 가지치기(pruning)를 수행하였다(Figs. 24, 25, 26, 27).
CART에 의한 분류회귀트리를 보면(Fig. 26), 대부분의 지하수함양량 추정에서 우선순위로 지형경사(SLOP)가 고려되었던 것을 확인할 수 있다. 그 다음으로는 강우(PCP)와 지형고도(DEM)이며 위성영상 촬영 일자별로 토양-식생관련 지수의 순위가 바뀌면서 공간적인 함양량 분포가 결정되었다.
Table 11.
Confusion matrix for groundwater recharge in spring
Table 12.
Confusion matrix for groundwater recharge in autumn
Table 13.
Analysis of error between prediction of recharge according to Landsat-8 OLI data and observation of monthly averaged groundwater recharge using SWAT-MODFLOW by season
Table 14.
Analysis of error for recharge zone in the CART algorithm
그 결과, 전반적인 정확도(Overall accuracy)는 0.5~0.7로 나타났으며 공간분포에 대한 Kappa계수는 0.3~0.6으로 나타났다. Kappa계수에 대한 코엔의 기존 해석으로는 양호~적당한 것으로 평가되지만, 코엔의 해석이 관대하게 평가되고 있다(McHugh, 2012). 따라서 결정계수값과 비교할 수 있도록 McHugh(2012)가 제안한 결과로 적용하면 위성영상을 사용하여 CART모형을 통해 추정한 함양량의 시공간적 분포는 통계적으로 상관성이 있게 예측이 가능한 것으로 판단된다.
향후 SWAT-MODFLOW의 입력값으로 위성영상결과를 적용하여 함양량을 산정한다면, 위성영상 분석결과와 기상, 지형인자에서 예측한 함양량의 Kappa계수값은 더 개선될 것으로 예상되며 이를 통해 위성영상을 통한 함양량 연구가 활발해 질 것으로 기대한다.
결 론
지하수함양은 매우 다양한 변수들이 서로 작용하여 복잡한 과정을 거치기 때문에 이를 직접적으로 측정하기 어렵다. 따라서 지하수함양의 시공간적 분포를 제시할 수 있는 수치모델링 접근 방법 중 하나인 SWAT-MODFLOW의 결과를 바탕으로 지하수함양량과 위성영상간의 상관성을 분석하였다.
빈도분석 결과 지하수함양량 분포 대비 토양-식생관련 지수와 강우, 지형인자 중에서 수정 수직식생지수(mPVI)와 지형경사(SLOP)는 정규분포를 나타내는 반면, 나머지 인자들은 비정규 분포양상을 띠고 있다. 회귀분석 결과 지하수함양량 대비 NDVI와 NDTI 그리고 지형경사(SLOP)는 매우 유익한 양의 상관성을 나타내고 있다.
김천지역에 대한 위성영상 분석을 통해 토양-식생 관련식(BSL)을 추정한 결과, 기울기는 약 0.815~1.506의 범위를 나타내고 있고, 절편은 약 -0.035~-0.000013의 범위였다. 지난 2005~2013년 동안 월평균 지하수함양량이 상대적으로 증가하는 3월과 11월에는 Red 밴드가 약 0.138, 0.079로 나타나 다른 기간에 비해 약 2~8배 정도 증가하는 것으로 나타났다.
복잡한 함양과정을 단순화하여 위성영상과 강우, 지형인자로부터 지하수함양량을 추정하기 위해 분류회귀트리(CART) 모형을 적용한 결과, 함양의 공간분포에 지배적인 영향인자는 지형경사(SLOP)와 강우(PCP)이며 지형고도(DEM)와 토양-식생관련 지수가 시기별로 지하수함양에 다양하게 영향을 주는 것으로 판단된다.
기존의 선행연구를 보면, 강우량이 300 mm 이상인 2003년 인도 서부지방에서 지하수 함양과 NDVI의 그래프는 결정계수 0.8 이상의 포물선 형태의 상관성을 나타내고 있지만, 장성지역에서 적용했던 지하수함양량과 토양-식생 관련 지수의 상관성 그래프에서 결정계수값은 최대 0.2 이하로 나타나 시공간별로 복잡한 토양-식생 분포 양상을 보이는 국내에서는 상대적으로 NDVI의 상관성이 다소 낮은 것으로 판단된다. 따라서 복잡한 함양과정을 단순화하여 분포시키는 수단으로 기계학습법의 하나인 CART모형을 사용하여 시기별 토양과 식생, 강우와 지형인자를 입력변수로 트리모형을 적절히 가지치기(pruning)한 결과 전반적인 정확도(Overall accuracy)가 0.5~0.7, 카파계수가 0.3~0.6으로 나타나 합리적으로 지하수 함양량 예측이 가능하다고 판단된다.