Review of Quantification of Fracture Characteristics Based on Topological Analysis

Hyorok Son; Young-Seog Kim

doi:10.9720/kseg.2021.1.001

Preview

Review

The Journal of Engineering Geology. 31 March 2021. 1-17
https://doi.org/10.9720/kseg.2021.1.001

Review of Quantification of Fracture Characteristics Based on Topological Analysis

위상기하 분석법을 이용한 단열계 특성 정량화의 소개

Hyorok Son¹

Young-Seog Kim²^*

손 효록¹

김 영석²^*

¹Master Course, Department of Earth & Environmental Sciences, Pukyong National University

²Professor, Department of Earth & Environmental Sciences, Pukyong National University

¹부경대학교 지구환경과학부 석사과정

²부경대학교 지구환경과학과 교수

^{*Corresponding Author}

ABSTRACT

It is important to evaluate the fracture network in a rock volume because fractures control the ground conditions and fluid flow characteristics. Therefore, various attempts have been made to quantify fracture networks to better understand ground and flow conditions. The use of fracture density alone (a quantitative parameter based on geometric analysis) does not fully explain the evolution of fracture networks, or quantify the spatial relationship (e.g. connectivity) of fractures in a rock mass. Therefore, the need for fracture network characterization based on topological analysis has recently emerged. In Korea however, the topological analysis of fracture networks within a rock mass has rarely been studied. As such, the definition of the topological analysis of fracture networks and the graph theory related to the topological analysis are briefly summarized in this study. We also introduce an application method for these analyses to fracture characterization. If the topological method is used for the analysis of fracture networks, it can also be adopted to analyze fluid flow characteristics of groundwater, characterize petroleum reservoirs, and analyze the evolution of a fracture network. In addition, topological analysis can be useful for site selection of major facilities such as nuclear waste disposal sites because it can be used to evaluate the stability of the potential sites.

Keywords

fracture network

topology

graph theory

fracture connectivity

fluid flow

암체 내에 발달하는 단열계는 지반의 특성뿐만 아니라 유체의 유동특성을 제어하기 때문에 이들을 평가하는 것은 매우 중요하다. 따라서 이들을 정량화하기 위한 다양한 시도가 있어왔다. 그러나 기하학적 분석을 통해 획득한 정량적 매개변수인 단열밀도만으로는 단열계의 진화를 설명하기 어렵고, 단열계의 연결패턴 같은 암석 내 단열의 공간적 관계를 정량화하기 어렵다. 따라서 최근 기존에 이뤄지던 기하학적 분석과 함께 위상기하 분석을 통한 단열계의 특성화 필요성이 대두되고 있다. 그러나 암체에의 다양한 적용성에도 불구하고, 아직 국내에서는 단열계의 위상기하 분석이 지질매체에 적용되어 연구된 적은 거의 없다. 따라서 본 연구에서는 최근 단열연구 분야에서 주목받고 있는 단열계 위상기하 분석의 정의와 개념, 위상기하 분석과 관련된 그래프이론, 그리고 이들을 적용하는 방법에 대해 간략히 소개하고자 한다. 이러한 위상기하학적 연구방법이 단열계의 분석에 사용된다면 암체 내 단열을 따라 흐르는 지하수나 석유 저류암의 유동특성과 단열계의 진화를 정량화하는데 유용하게 사용될 수 있다. 또한 방사성폐기물처분장과 같이 유체의 유동특성이 중요한 주요 시설물의 부지선정 등에 유용하게 활용될 수 있을 것이다.

키워드

단열계

위상기하학

그래프이론

단열 연결성

유체유동

MAIN

서 론
단열계의 위상기하
단열계의 연결성
단열계의 밀집성(abundance)
단열계의 위상기하와 그래프이론
단열계의 위상기하를 이용한 연구사례
정단층의 특성 분석
단열계의 구조적 복잡성과 지하수 유동 사이의 관계 분석
단열계 내 공간적 특성의 다양성 분석
단층손상대 유형별 연결성과 배열의 정량화
프로그램을 이용한 단열계의 위상기하학 분석
토 의
단열계의 3차원 위상기하 분석
단열계의 위상기하에 영향을 미치는 요인
결 론

서 론

암체 내 구조적 불연속면인 단열은 암석의 강도, 투수성, 공극률 같은 물리적 속성을 제어한다(Adler and Thovert, 1999). 또한 단열은 암체 내에서 개별로 존재하지 않고 여러 개 단열의 집합인 단열계로 존재해 서로 영향을 미치며 주변 단열과의 관계에 의해 복잡한 패턴을 이루면서 존재한다. 따라서 단열계 패턴의 특성화는 사면 안정성 조사(Clarke and Burbank, 2011; Krabbendam and Glasser, 2011), 암체 내 유체의 거동특성 조사(Berkowitz and Balberg, 1993; Adler and Thovert, 1999; Jolley et al., 2007; Singhal and Gupta, 2010), 이산화탄소의 지중저장(Odling et al., 1999; Bisdom et al., 2014; Pérez-Flores et al., 2017) 등에 이용되었다. 기존 연구에서는 한 단열계를 특성화 할 때 그들의 기하학적 특성(단열의 개수, 길이, 자세 등)만을 분석하였지만, 최근 들어서 단열 간 공간적 관계를 설명하기 위해 기존의 기하학적 분석과 함께 위상기하학적 분석이 이뤄지고 있다(Sanderson and Nixon, 2015, 2018). 또한 단열 혹은 단층의 배열진화를 설명하기 위해서도 위상기하학적 분석이 사용되기도 한다(Duffy et al., 2017; Laubach et al., 2018; Nixon et al., 2020).

위상기하학은 공간적 객체 간의 배열과 기하학적 관계를 설명하는 수학의 한 분야이며, 객체가 존재하는 공간의 연속적인 변형(찢어지는 변형을 제외한 변형, 예로 늘이거나 줄이는 변형)에 대해 변하지 않는 속성을 연구하는 학문이다. 연속적인 변형에 대해 객체의 기하학적 특성(길이, 면적 등)은 변할 수 있지만, 위상기하학적 특성(연결 개수 등)은 변하지 않는다. 이런 위상기하학적 특징을 바탕으로 단열계를 특성화 하면 스케일에 따라 변하지 않는 무차원 매개변수를 구할 수 있다(Jing and Stephansson, 1997; Sanderson and Nixon, 2015).

단열계의 위상기하적 분석은 단열계의 연결성을 정량화하여 유체의 투수성을 설명할 수 있기 때문에, 암체 내에서 유체의 유동특성과 석유의 구조적 트랩 등을 연구할 때 유용하게 이용될 수 있고, 유체의 거동특성이 중요한 방사성폐기물처분장의 부지선정에도 이용될 수 있다. 또한 같은 단열밀도를 가지거나 같은 기하학적 특징을 가지는 두 단열계라 하더라도 다른 연결성을 가지면 다른 위상기하학적 특징을 보이기 때문에 위상기하학적 분석이 유용하게 이용될 수 있다. 이와 같은 이유에서, 단열계의 특성을 정의 할 때, 기존의 기하학적 분석과 위상기하학적 분석이 함께 이뤄져야 한다는 주장이 부각되고 있다(Sanderson and Nixon, 2015).

단열계를 특성화하는 데 도움이 되는 위상기하학적 분석의 유용성에도 불구하고, 아직 우리나라에서는 위상기하학적 분석의 초보적인 개념과 소개(Son and Kim, 2020) 이외에는 위상기하학적 분석이 지질매체에 적용되어 연구된 적은 거의 없다. 따라서 이 논문에서는 위상기하에 대한 정의와 적용에 대해 간략히 정리하고, 현재까지 이루어진 단열계 특성화에 이용된 위상기하학적 연구들을 소개하고자 한다.

단열계의 위상기하

2차원에서, 단열계의 위상기하는 한 단열의 트레이스인 단열선(line), 노드(node), 노드 사이를 잇는 브랜치(branch)로 이뤄진 네트워크로 설명한다(Fig. 1a; Sanderson and Nixon, 2015). 단열 간 관계에 기초하여 노드는 단열의 말단을 나타내는 I-노드, 한 단열이 분기하거나 다른 단열에 붙는 관계를 나타내는 Y-노드, 두 단열이 교차 절단하는 관계를 나타내는 X-노드, 이렇게 세 가지 유형으로 구분되며(Manzocchi, 2002), 이중 I-노드는 독립된 노드, X-노드와 Y-노드는 연결된 노드로 분류된다. 브랜치는 이들의 양 끝에 위치하는 노드의 유형에 기초하여 양 끝 모두 독립된 노드가 있는 II-브랜치(II-), 한 쪽 끝에만 연결된 노드가 있는 IC-브랜치(IY-, IX-), 양 끝 모두 연결된 노드가 있는 CC-브랜치(YY-, YX-, XX-), 이렇게 크게 세 가지(혹은 여섯 가지) 유형으로 구분 된다(Sanderson and Nixon, 2015). 노드(I-, Y-, X-) 혹은 브랜치(II-, IC-, CC-)의 각 유형별 개수의 비율을 구해 삼각형의 세 꼭짓점이 각 유형를 나타내는 삼각도표에 각각의 비율 작도하면 단열계의 연결성에 대한 정보를 얻을 수 있다(Fig. 1b; Manzocchi, 2002). 또한 노드와 브랜치의 각 유형별 개수를 수학적으로 조합하여 단열계의 연결성을 정량화하는 매개변수를 구할 수 있다(Manzocchi, 2002; Sanderson and Nixon, 2015).

https://static.apub.kr/journalsite/sites/kseg/2021-031-01/N0520310101/images/kseg_31_01_01_F1.jpg

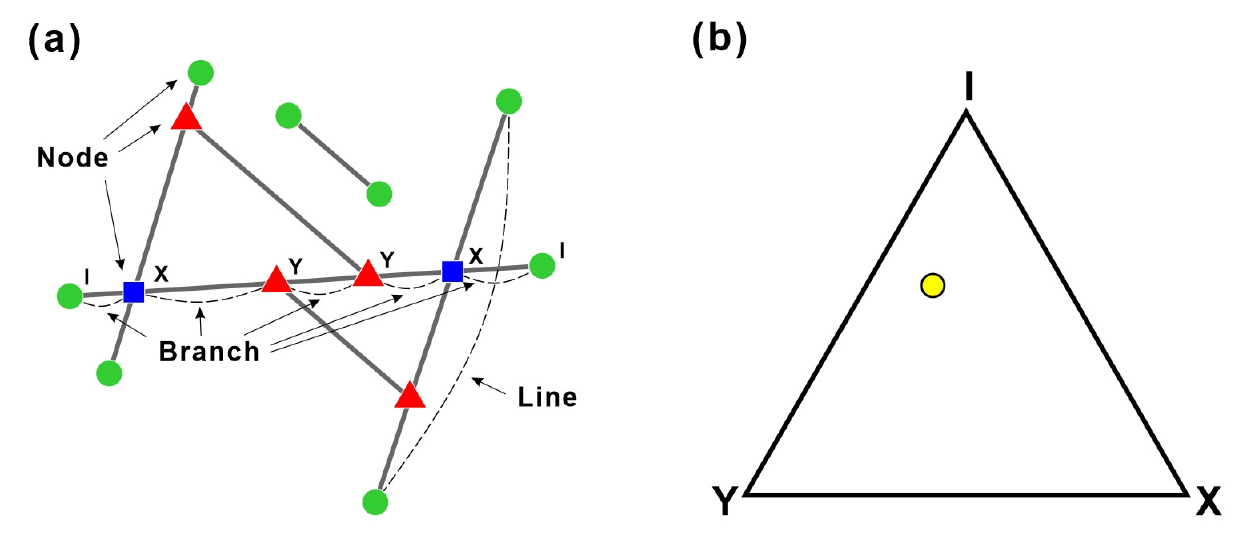
Fig. 1

Terminology of node and branch model (modified from Nyberg et al., 2018). (b) The triangular plot of a relative number of nodes in (a) (after Manzocchi, 2002).

단열계의 연결성

노드의 각 유형별 개수를 세어 구할 수 있는 첫 번째 매개변수는 총 브랜치 개수(N_B)와 총 단열선 개수(N_L)의 비율(N_B/N_L)이다. 한 개의 단열선은 두 개의 종단 노드(I-노드 혹은 Y-노드)를 가져 총 단열선 개수(N_L)는 다음과 같이 계산된다(Sanderson and Nixon, 2015).

(1)

N_{L} = 1 / 2 (N_{I} + N_{Y})

식 (1)에서, N_I은 I-노드의 개수, N_Y는 Y-노드의 개수다. 한 개의 브랜치는 두 개의 노드를 가지고, I-노드는 한 개의 브랜치, Y-노드는 세 개의 브랜치, X-노드는 네 개의 브랜치를 가져 총 브랜치의 개수(N_B)는 다음과 같이 계산된다(Sanderson and Nixon, 2015).

(2)

N_{B} = 1 / 2 (N_{I} + 3 N_{Y} + 4 N_{X})

식 (2)에서, N_X는 X-노드의 개수다. 따라서 총 브랜치 개수와 총 단열선 개수의 비율(N_B/N_L)은 다음과 같다(Sanderson and Nixon, 2015).

(3)

N_{B} / N_{L} = 1 / 2 (N_{I} + 3 N_{Y} + 4 N_{X}) / 1 / 2 (N_{I} + N_{Y}) = (N_{I} + 3 N_{Y} + 4 N_{X}) / (N_{I} + N_{Y})

또한 각 노드 유형의 비율을 P_I, P_Y, P_X라고 설정하고, P_I, P_Y, P_X의 합은 1이기 때문에 총 브랜치 개수와 총 단열선 개수의 비율(N_B/N_L)을 다음과 같이 나타낼 수 있다(Sanderson and Nixon, 2015).

(4)

N_{B} / N_{L} = (P_{I} + 3 P_{Y} + 4 P_{X}) / (P_{I} + P_{Y}) = (4 - 3 P_{I} - P_{Y}) / (P_{I} + P_{Y})

총 브랜치 개수와 총 단열선 개수의 비율(N_B/N_L)을 노드 삼각도표에 표시한 Fig. 2a를 보면 단열계의 위상기하에 따라 총 브랜치 개수와 총 단열선 개수의 비율(N_B/N_L)이 변함을 확인 할 수 있다. 단열계에 I-노드를 가지는 고립된 단열들이 많다면 N_B/N_L이 1에 근접하고, Y-노드를 가지는 분기(splay)하거나 붙는(abut) 단열들이 많다면 N_B/N_L이 3에 근접하고, X-노드를 가지는 서로 교차하는 단열들이 많다면 N_B/N_L이 무한까지 이를 수 있다(Fig. 2a; Sanderson and Nixon, 2015).

https://static.apub.kr/journalsite/sites/kseg/2021-031-01/N0520310101/images/kseg_31_01_01_F2.jpg

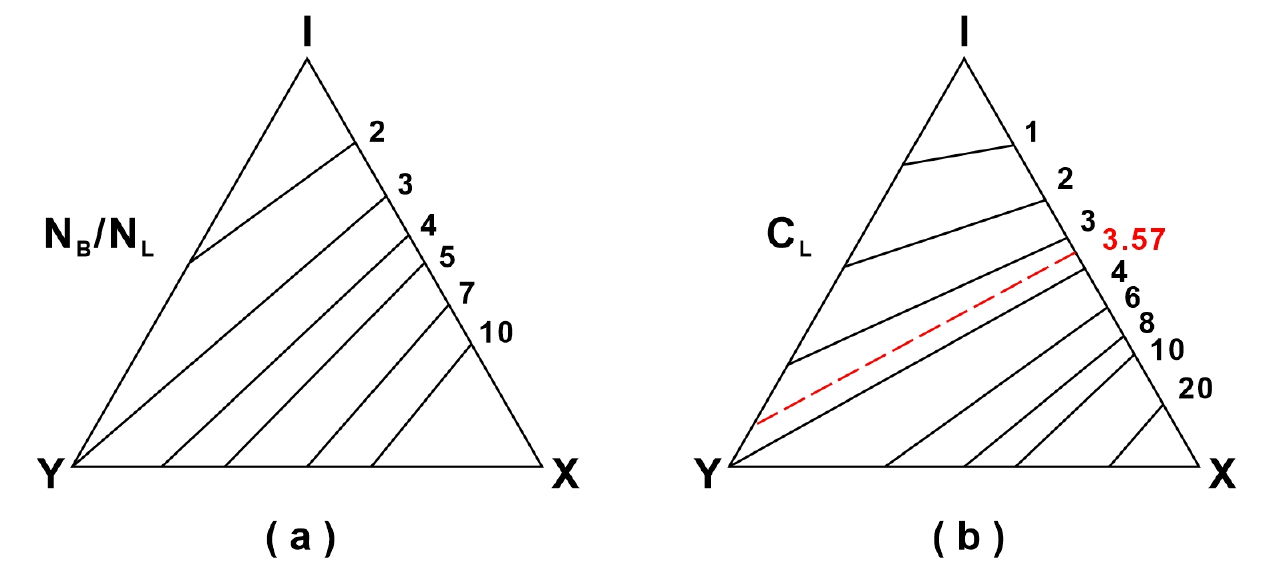
Fig. 2

Triangular plots of a relative number of nodes. (a) Ratio of the number of branches to lines (N_B/N_L). (b) Average number of connections per line (C_L) (modified from Sanderson and Nixon, 2015). The value of 3.57 means that the fracture network is well connected.

두 번째 매개변수는 단열선 당 평균 연결 개수(C_L)이다. 노드의 유형 중에서 Y-노드와 X-노드는 연결된 노드이고, 한 개의 노드는 두개의 단열선을 연결하기 때문에 단열선 당 평균 연결 개수(C_L)는 다음과 같이 계산된다(Sanderson and Nixon, 2015).

(5)

C_{L} = 2 (N_{Y} + N_{X}) / N_{L}

또한 식 (5)에 총 단열선 개수 N_L = 1/2(N_I+N_Y)를 대입하고, 각 노드의 수를 비율로 치환하면 다음과 같이 나타낼 수 있다(Sanderson and Nixon, 2015).

(6)

C_{L} = 2 (N_{Y} + N_{X}) / 1 / 2 (N_{I} + N_{Y}) = 4 (N_{Y} + N_{X}) / (N_{I} + N_{Y}) = 4 (P_{Y} + P_{X}) / (P_{I} + P_{Y})

단열선 당 평균 연결 개수(C_L)를 노드 삼각도표에 표시한 Fig. 2b를 보면 단열계의 위상기하에 따라 단열선 당 평균 연결 개수(C_L)가 변함을 확인 할 수 있다. Balberg et al.(1984)은 일정한 길이를 가지는 단열선의 무작위 배열에서 연결된 단열선의 집합체인 클러스터가 샘플영역을 가로지르며 관통하는 침투임계점에서 단열선 당 평균 연결 개수(C_L)가 3.57임을 보여줬다. 또한 연결된 네트워크를 형성하기 위해서, 하나의 단열선은 다른 두 단열선에 연결되어야하기 때문에 C_L이 2 이하인 단열계는 연결된 네트워크가 없음을 뜻한다(Sanderson and Nixon, 2018).

세 번째 매개변수는 브랜치 당 평균 연결 개수(C_B)이다. 노드의 유형 중에서 Y-노드와 X-노드는 연결된 노드이고, Y-노드는 3개의 브랜치를, X-노드는 4개의 브랜치를 가지기 때문에 브랜치 당 평균 연결 개수(C_B)는 다음과 같이 계산된다(Sanderson and Nixon, 2015).

(7)

C_{B} = (3 N_{Y} + 4 N_{X}) / N_{B}

한 개의 브랜치는 두 개의 노드를 가지기 때문에 브랜치 당 평균 연결 개수(C_B)는 0~2의 값을 가진다. 또한 브랜치의 종단이 독립된 노드일 확률을 P_I = N_I/(N_I+3N_Y+4N_X), 연결된 노드일 확률을 P_C = (3N_Y+4N_X)/(N_I+3N_Y+4N_X)라고 하면, 각각의 브랜치 유형의 확률은 아래와 같이 계산된다(Sanderson and Nixon, 2015).

(8)

P_{I I} = {P_{I}}^{2}, {P_{I}}_{C} = P_{I} P_{C}, P_{C C} = {P_{C}}^{2}

이렇게 구해진 확률은 브랜치 삼각도표에 하나의 선으로 표시된 C_B를 따라 표시된다. 브랜치 삼각도표에서, 단열계에 II-브랜치가 많다면 C_B는 0에 근접하고, IC-브랜치, CC-브랜치가 많아지며 2에 근접하는 것을 알 수 있다(Fig. 3a).

https://static.apub.kr/journalsite/sites/kseg/2021-031-01/N0520310101/images/kseg_31_01_01_F3.jpg

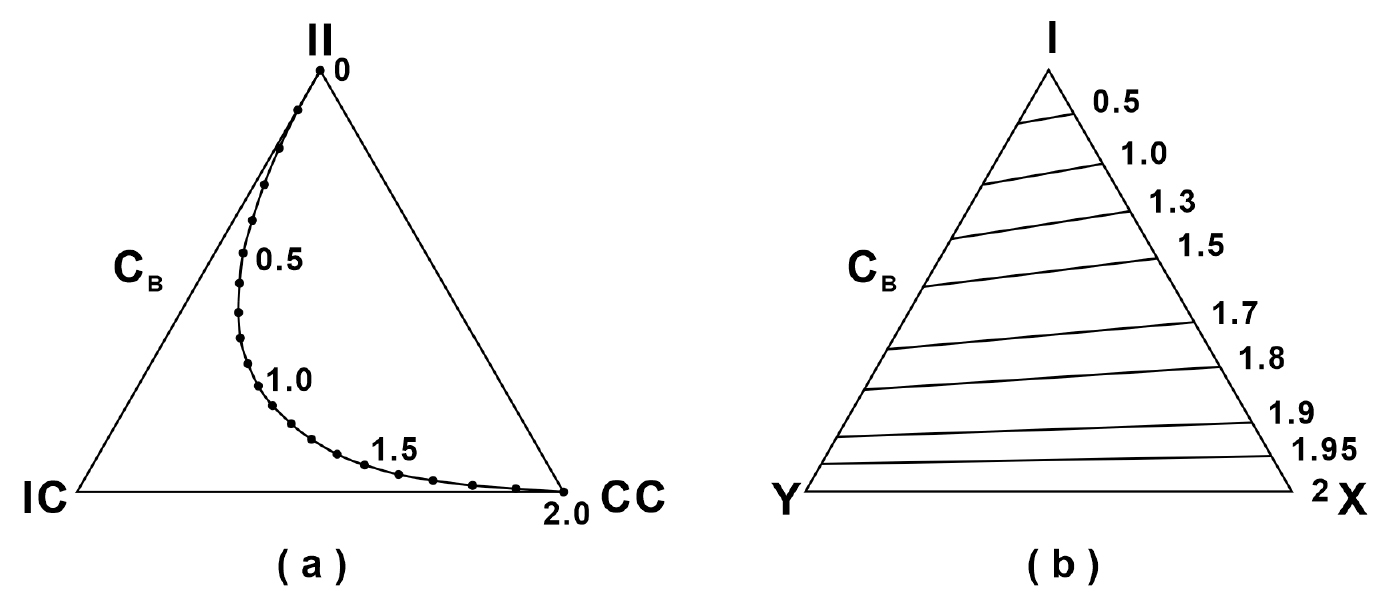
Fig. 3

(a) Triangular plots of the relative number of each branch type with average number of connections per branch (C_B). (b) Triangular plots of the relative number of nodes with average number of connections per branch (C_B) (modified from Sanderson and Nixon, 2015).

앞서 소개한 단열계의 연결성을 나타내는 매개변수 중, 단열계의 단열선에 기초한 매개변수(N_B/N_L, C_L)보다 브랜치에 기초한 매개변수(C_B)가 유용하게 이용된다. 이는 브랜치에 기초한 매개변수는 일정 범위가 아닌 특정한 값을 지시하기 때문이다. 예를 들면, 대부분 CC-브랜치로 이뤄진(노드 삼각도표에서 YX축에 표시되는) 단열계에서, 단열선에 기초한 매개변수(N_B/N_L, C_L)는 다양한 값을 가질 수 있는 반면(Fig. 2), 브랜치에 기초한 C_B는 2에 근접하는 값을 가지는 것을 알 수 있다(Fig. 3). 또한 브랜치가 단열선보다 식별하기 쉽다는 점, 단열선 길이보다 같거나 짧아 원형 샘플링에 의해 절단되는 정도가 적다는 점, 단열선 길이 분포보다 평균값에 더 집중된 분포를 가진다는 점을 이유로 브랜치에 기초한 매개변수가 유용하게 이용될 수 있다(Sanderson and Nixon, 2015).

단열계의 밀집성(abundance)

노드의 유형별 개수를 세어 단열계의 밀집성을 지시하는 매개변수도 구할 수 있다. 2차원의 단면에서, 단열계의 밀집성을 지시하는 매개변수에는 단위면적 당 단열선의 개수를 나타내는 2차원 단열밀도(P₂₀, 2D fracture density), 단위면적 당 단열선의 길이를 나타내는 단열강도(P₂₁, fracture intensity), 단위면적 당 단열선이 이루는 면적을 나타내는 무차원 단열강도(P₂₂, dimensionless intensity)가 있으며 각각은 아래의 식으로 계산된다(Sanderson and Nixon, 2015).

(9)

P_{20} = N_{L} / A [L^{- 2}], P_{21} = \sum L / A [L^{- 1}], P_{22} = N_{L} {L_{C}}^{2} / A = P_{21} L_{C} (N_{L} L_{C} / A = P_{21})

식 (9)에서, A는 샘플링 면적이고 L_C는 특성 길이로 단열선 길이의 산술평균을 나타내며, 아래의 식으로 계산된다.

(10)

L_{C} = \sum L / N_{L}

앞서 말했듯이 단열선 길이는 샘플링 범위를 벗어나는 경우가 많아 절단되는 경우가 많기 때문에 단열계의 브랜치 길이로 매개변수를 구하는 것이 더 유용하다. 따라서 단열계의 브랜치 길이로 구한 매개변수 식은 아래와 같다(Sanderson and Nixon, 2015).

(11)

B_{20} = N_{B} / A [L^{- 2}], B_{21} = \sum L_{B} / A [L^{- 1}] = N_{B} B_{C} / A, B_{22} = N_{B} {B_{C}}^{2} / A = B_{21} L_{C} (N_{B} B_{C} / A = B_{21})

단열계의 단열선과 브랜치 길이의 합은 같기 때문에, B₂₁ = P₂₁이다.

단열계의 위상기하와 그래프이론

그래프이론은 노드(꼭짓점)와 브랜치(빗변)로 구성된 그래프의 특성을 연구하는 수학의 한 분야이다(Sanderson et al., 2019). 한 단열계를 하나의 그래프로 간주하면 단열선(line)은 하나 이상의 브랜치로, 단열선의 말단과 교차점을 노드로 볼 수 있다. 단열계 특성화에 그래프 이론을 적용하면 단열계를 이루는 그래프 원소(노드, 브랜치, 영역, 연결요소)들의 관계를 오일러식을 통해 알 수 있다. 또한, 그래프는 단열계의 기하와는 독립된 성질을 갖지만 단열계의 위상기하와는 연관지어 설명 할 수 있다(Sanderson et al., 2019).

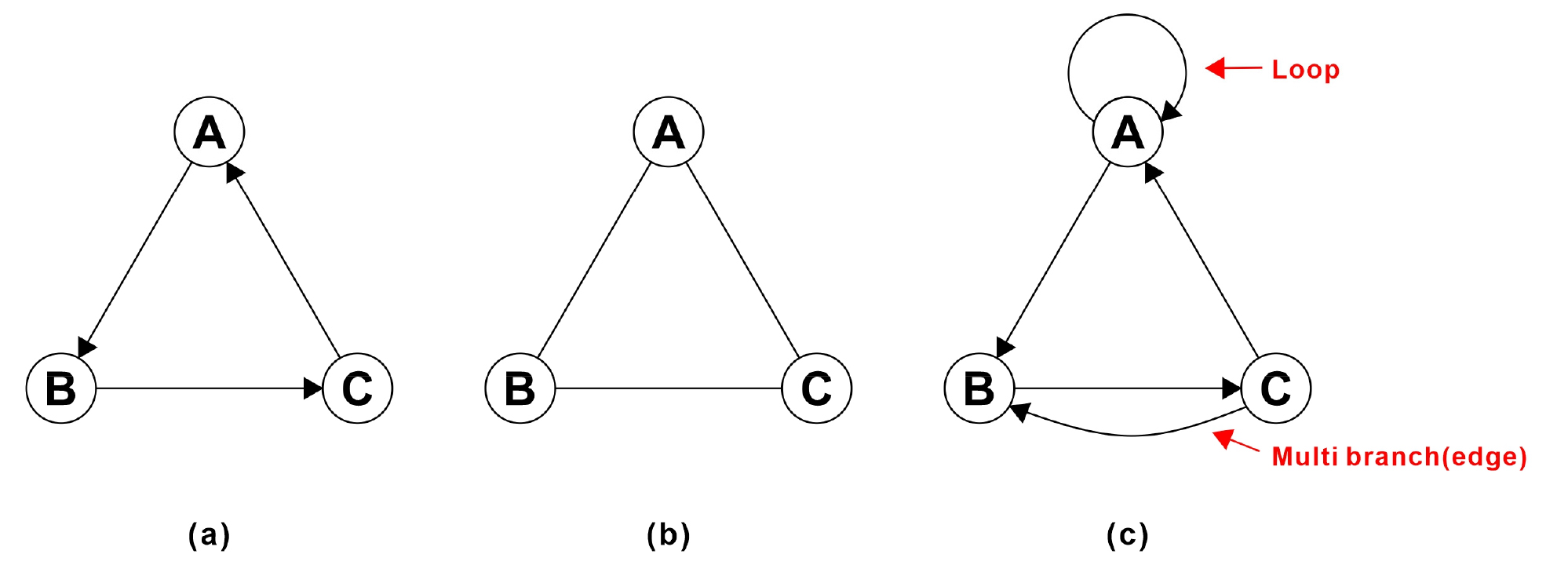
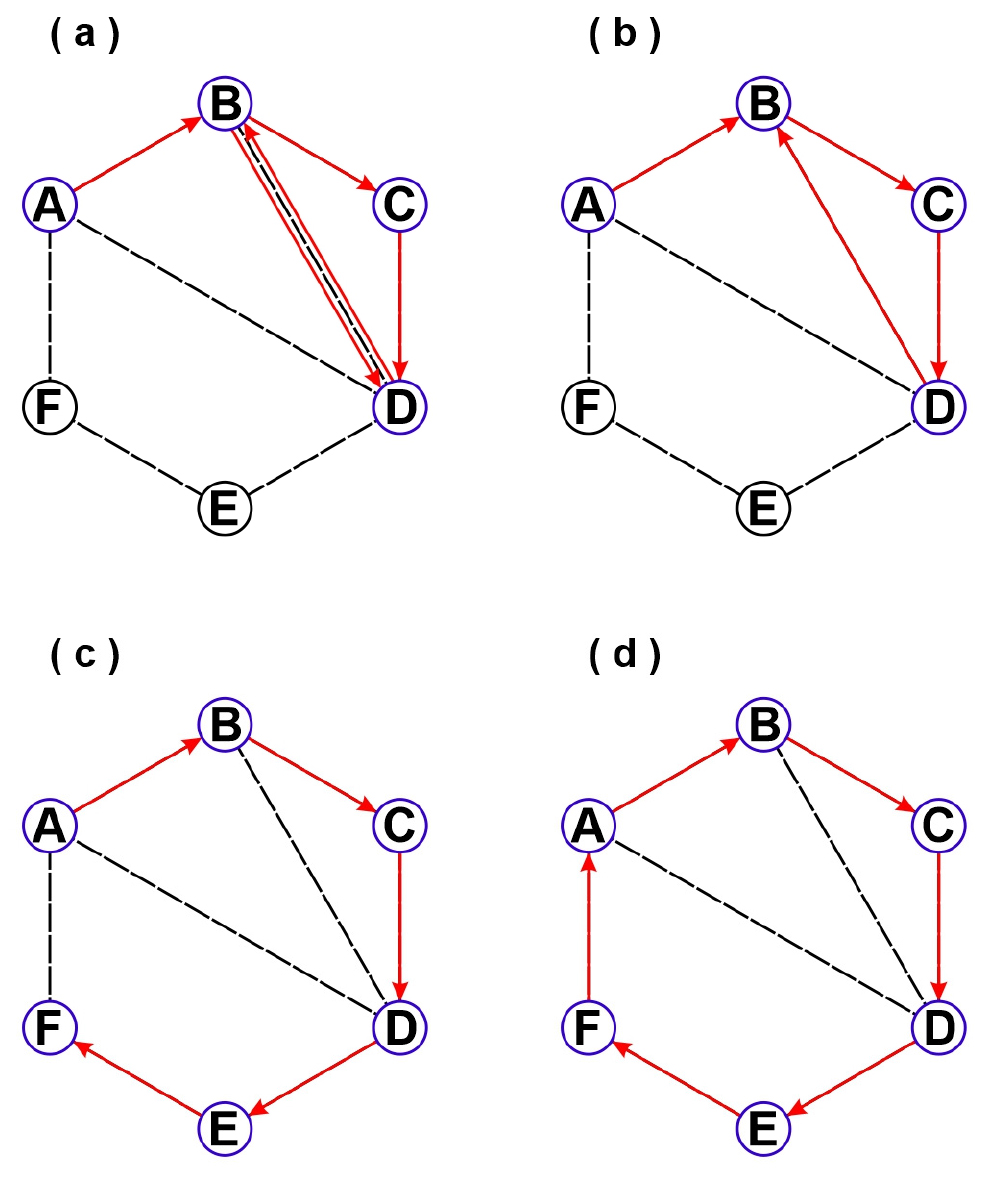
그래프는 노드를 횡단하는 방향의 유무에 따라 유향그래프(directed graph)와 무향그래프(undirected graph)로 나뉜다. 단열계는 무향그래프 중 루프(loop)가 없고 멀티 브랜치(multi branches)가 없는 단순무향그래프(simple undirected graph)로 간주한다(Fig. 4). 또한 단열계는 2차원 평면에서, 브랜치가 노드에서만 만나는 평면그래프(planar graph)로 간주한다. 그래프에서, 인접한 노드를 횡단하는데 네 가지 방법이 있다. 보행(walk)은 인접한 노드를 횡단하는 것이고(Fig. 5a의 ABCDBD), 브랜치를 반복하지 않는 보행을 트레일(trail, Fig. 5b의 ABCDB), 브랜치와 노드를 반복하지 않는 보행을 경로(path, Fig. 5d의 ABCDEF)라고 한다. 마지막으로 순환(cycle, Fig. 5d의 ABCDEFA)은 횡단을 시작하는 노드와 횡단을 종료하는 노드가 같은 경로를 말한다. 또한 노드와 브랜치는 영역(regions)과 연결요소(connected components)을 형성하는데, 영역은 순환으로 둘러싸인 다각형이고, 연결요소는 하나 이상의 경로를 가지는 연결된 노드와 브랜치의 집합체이다(Fig. 6c).

https://static.apub.kr/journalsite/sites/kseg/2021-031-01/N0520310101/images/kseg_31_01_01_F4.jpg

Fig. 4

Examples of a directed graph (a), an undirected graph (b), and a directed graph with a loop and a multi branch (c).

https://static.apub.kr/journalsite/sites/kseg/2021-031-01/N0520310101/images/kseg_31_01_01_F5.jpg

Fig. 5

Examples of traversing adjacent nodes. (a) Walk (ABCDBD), (b) trail (ABCDB), (c) path (ABCDEF), and (d) cycle (ABCDEFA).

https://static.apub.kr/journalsite/sites/kseg/2021-031-01/N0520310101/images/kseg_31_01_01_F6.jpg

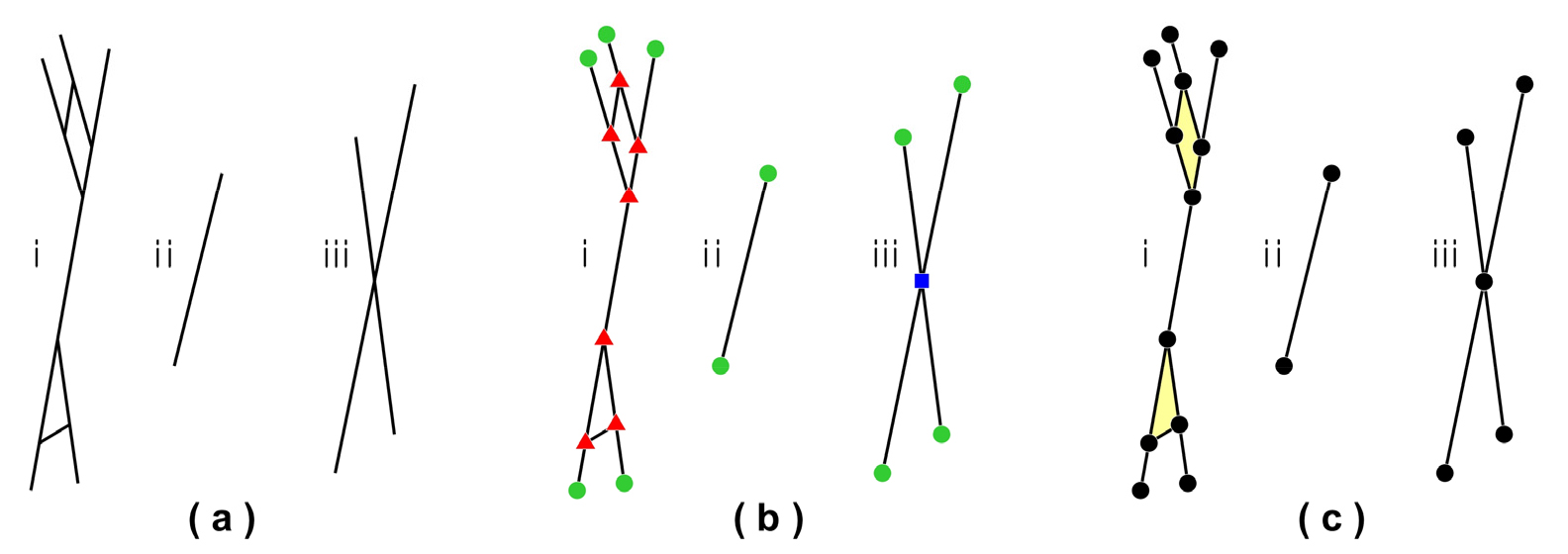
Fig. 6

(a) Trace map of fracture network with three connected components (i–iii). (b) Node and branch model of (a), notation as in Fig. 1a. (c) Graph features (node, branch, connected components, regions) of (a) (modified from Sanderson et al., 2019).

그래프 이론에서, 그래프의 연결성을 나타내는 매개변수는 평균노드차수(<d>, average degree of node)이다. 차수는 한 노드 당 연결된 브랜치 수를 뜻하며, 한 브랜치 당 두 개의 노드를 가지기 때문에 평균노드차수(<d>)는 아래와 같이 계산된다(Sanderson et al., 2019).

(12)

< d > = 2 | B | / | N |

식 (12)에서, B는 브랜치의 개수이고 N은 노드의 개수이다. I-노드가 많은 단열계의 경우 평균노드차수가 1에 근접하고, Y-노드가 많은 단열계는 3에 근접하고, X-노드가 많은 단열계의 경우 4에 근접한다(Fig. 7).

https://static.apub.kr/journalsite/sites/kseg/2021-031-01/N0520310101/images/kseg_31_01_01_F7.jpg

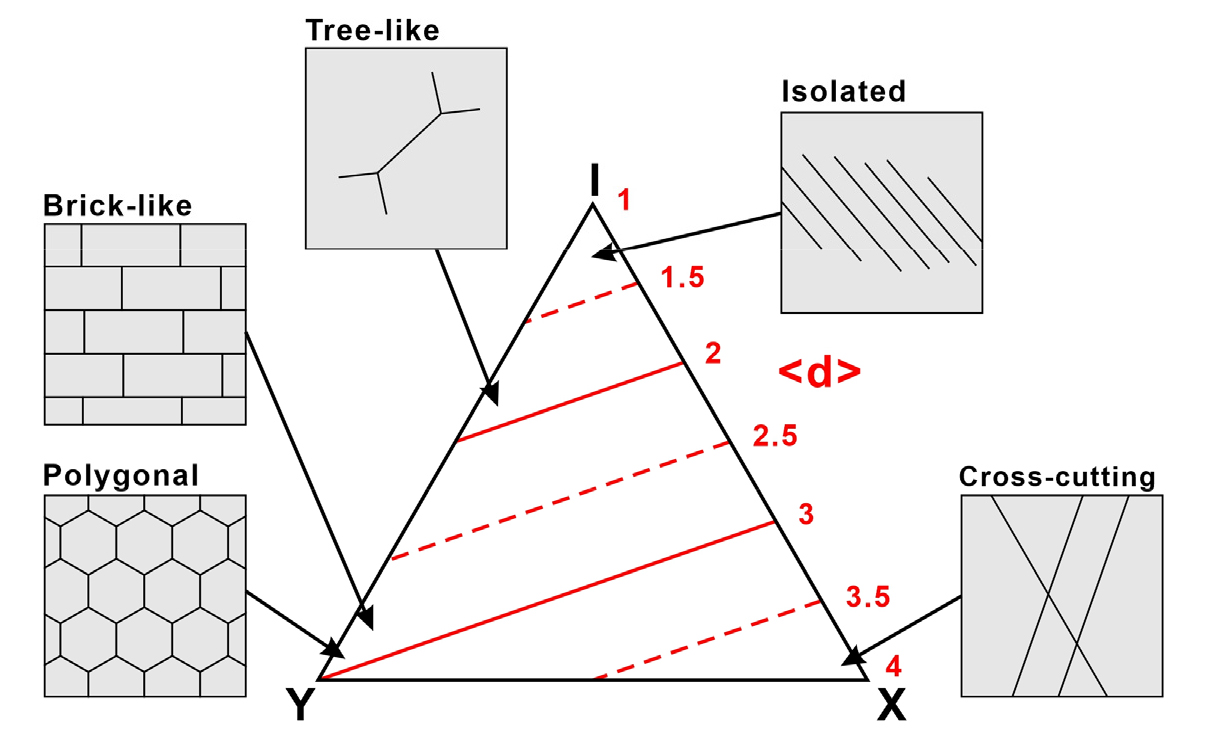
Fig. 7

Triangular plots of nodes with average degree of nodes (<d>) and examples of fracture networks showing the different average degree of nodes (<d>) (modified from Sanderson et al., 2019).

다면체에 적용되는 오일러 공식(Euler, 1758)으로 그래프를 이루는 네 가지 원소인 노드, 브랜치, 연결요소, 영역의 관계를 방정식으로 나타낼 수 있다. 평면그래프에서, 오일러 공식은 아래와 같다.

(13)

| N | - | B | + | R | - | K | = 0

식 (13)에서, B는 브랜치의 총 개수, N은 노드의 총 개수, R은 영역의 총 개수, K는 연결요소의 총 개수다. 식 (13)을 이용하여 단열계의 노드, 브랜치, 연결요소의 개수를 이용하여 영역 개수를 구할 수 있다. 샘플링되는 전체면적(A)을 알고 있다면 이를 영역 총 개수(R)로 나누어, 블록의 평균면적(A/R)을 구할 수 있다(Sanderson et al., 2019). 또한 블록의 평균면적을 샘플링 전체면적으로 나누어 단열에 의해 파괴된 정도를 나타내는 무차원블록강도(R₂₂, dimensionless block intensity)도 구할 수 있다(식 (14); Nixon et al., 2020).

(14)

R_{22} = A / R \times A^{- 1} = 1 / R

식 (14)에서, R은 노드와 브랜치로 둘러싸인 영역의 개수를 나타내므로 이 영역의 외부를 1로 두어 암체 전체를 나타내기 위해 식 (14)를 아래와 같이 변환할 수 있다.

(15)

R_{22} = 1 / R + 1

식 (15)에서, 무차원블록강도가 1에 가까우면 파쇄가 거의 없음을 나타내고, 0에 가까우면 파쇄가 많이 이뤄짐을 나타낸다(Nixon et al., 2020).

단열계의 위상기하를 이용한 연구사례

정단층의 특성 분석

Morley and Nixon(2016)은 단층계의 위상기하학적 특성과 등가네트워크(equivalent network) 특성을 바탕으로 12개의 정단층계를 7가지 유형으로 분류하였다. 여기에 이용된 특성에는 단층계의 각 노드 유형(I-, Y-, X-)별 비율, 단층계의 각 브랜치 유형(II-, IC-, CC-)별 비율, 단층의 분기 유형(splay(Ys), abut(Ya), cross-cut(Yc))별 비율, 단층계의 노드차수(d)의 분포, 브랜치 당 평균 연결 개수(C_B)가 이용되었다. 또한 이 분류를 바탕으로, 단층계가 진화하면서 여러 요인에 의해 단층계의 위상기하학적 특성이 변화함을 제시하였고, 이 요인에는 변형률의 증가, 기존에 존재하던 패브릭의 영향, 시간차를 두고 가해지는 주응력 사이의 각 등이 있다. 변형률이 증가하면서 단열계의 위상기하는 Y-노드, IC-브랜치, Ya-노드의 비율이 커지고, 연결성도 증가함을 보여주었으며 이는 단열계의 패턴이 비교적 복잡해짐을 뜻한다. 기존 약대(패브릭)의 영향이 커지면서 단열계의 위상기하는 Y-노드, IC- 및 CC-브랜치, Ya-노드의 비율이 커지고, 연결성도 증가함을 보여주었으며 이 또한 단열계의 패턴이 복잡해짐을 뜻한다. 이보다 더 많은 수의 기존 약대가 영향을 미친다면 이 값들이 다시 처음으로 되돌아가는 경향을 보인다. 이는 많은 수의 약대의 영향이 커진다면 단열계의 위상기하는 더 단순한 패턴을 가짐을 뜻한다. 첫 번째 주응력과 두 번째 주응력사이의 각도가 증가함에 따라 단열계의 위상기하는 Y-노드, IC- 및 CC-브랜치, Ya-노드(이후 Yc-노드까지)의 비율이 커지고, 연결성도 증가함을 보이며 단열계 패턴이 복잡해짐을 뜻한다. 이런 위상기하학적 분석이 기존의 단열계 특성화 방법을 보완할 수 있는 방법이다.

단열계의 구조적 복잡성과 지하수 유동 사이의 관계 분석

Dimmen et al.(2017)은 단열계의 위상기하분석과 공극률 분석을 이용하여 단열계에서 구조적으로 복잡한 영역과 유체유동사이 관계를 정량화하고 시각화하였다. 이들은 단열계를 따라서 발달하는 낮은 공극률을 가지는 고결된 마운드의 공간적 분포를 조사하고, 이들이 발달하는 단열계의 기하학적 특성(단열 밀도), 위상기하학적 특성(연결된 노드 빈도)의 공간적 분포를 조사하였다(Fig. 8). 단열들의 상호작용(relay, intersection 등)으로 형성된 구조적으로 복잡한 영역은 단열 밀도와 연결된 노드 빈도가 높은 영역과 일치함을 보이며, 이 영역은 연결성이 높음을 지시한다. 또한 이 영역과 마운드가 있는 영역이 일치함을 보여주었으며, 이는 구조적으로 복잡한 영역에서 유체유동의 증가로 유체와 암석 간 상호작용이 증가하여 고결작용이 더 많이 일어난 결과로 해석하였다.

https://static.apub.kr/journalsite/sites/kseg/2021-031-01/N0520310101/images/kseg_31_01_01_F8.jpg

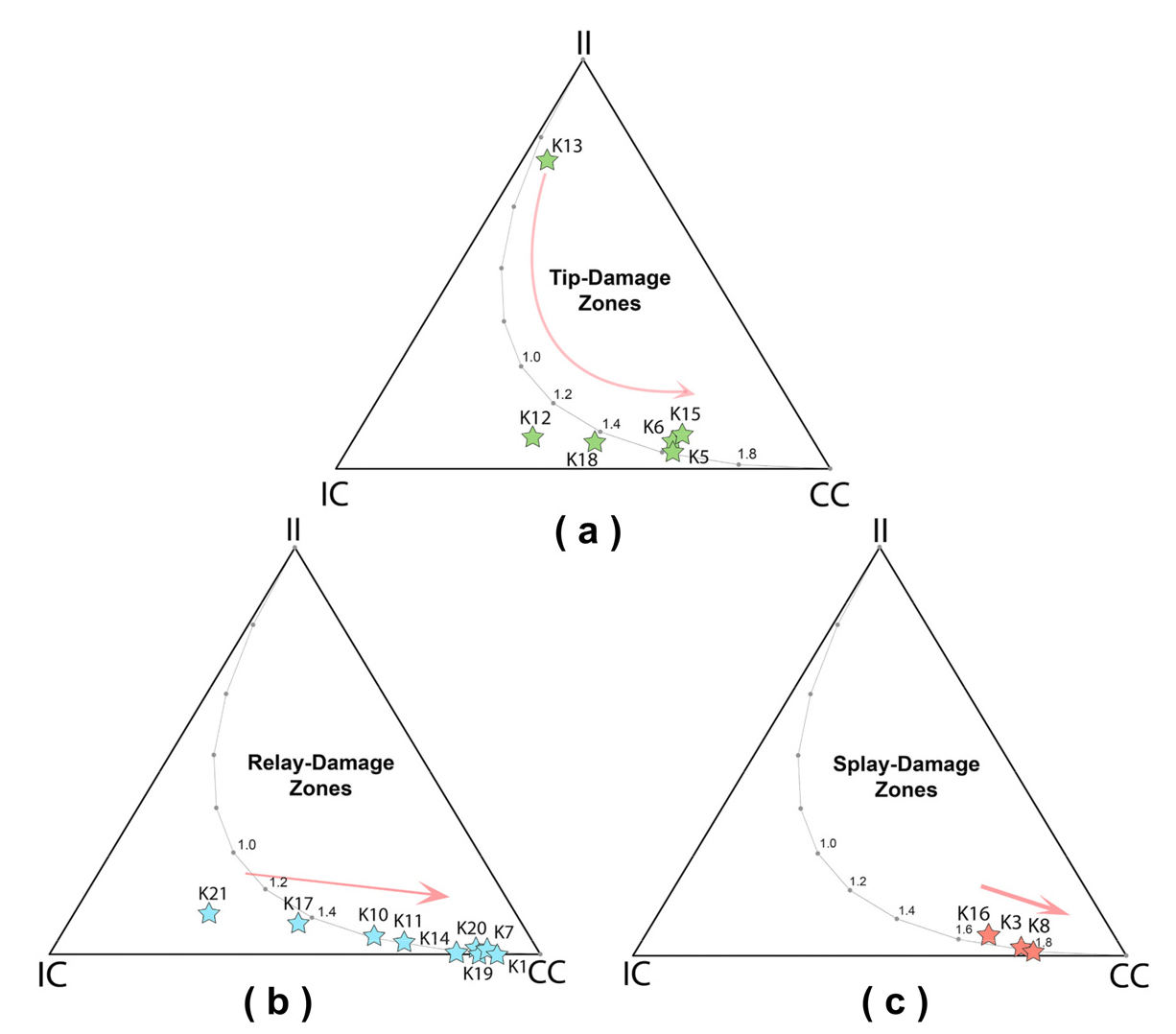
Fig. 8

One of the results of the study by Dimmen et al. (2017). (a) Digitized map of the fracture network (V2). (b) Contour map of fracture intensity showing the abundance of the fracture network. (c) Contour map of connecting node frequency showing the connectivity of the fracture network. (d) Graph of fracture intensity. (e) Graph of connecting node frequency. (f) Graph of topography profile along the fracture network. The mounds are related with the regions which have high fracture intensity and connecting node frequency (from Dimmen et al., 2017).

단열계 내 공간적 특성의 다양성 분석

Procter and Sanderson(2018)은 단열계의 원형 샘플링 면적 내 각 노드 유형의 수를 세어 위상기하 분석을 하였고, 원형 샘플선과 만나는 단열의 수를 세어 얻은 단열강도의 공간적 변산도(variability)를 분석하였다. 여기서 변산도는 측정값들의 분포가 얼마나 분산/밀집되었는지를 나타내는 통계치이다. 원형 샘플 선과 만나는 단열 개수를 세어 단열강도(P₁₀)를 계산하는 것은 샘플 원 면적 내 단열의 총 길이를 측정해 얻은 단열강도(P₂₁)를 계산하는 것은 보다 빠른 자료처리를 할 수 있다는 장점이 있으며, 이 둘은 거의 비슷한 정밀도를 가지고 있음을 확인하였다. 또한 ANOVA test를 이용하여 단열이 발달하는 한 층 내에서 또는 다른 층 사이에서 그리고 지역(공간)별로 단열강도(P₁₀)의 변산도를 분석하였고, 이를 바탕으로 연구지역 단열밀도의 공간적 매핑을 실시하였다.

단층손상대 유형별 연결성과 배열의 정량화

Nixon et al.(2020)은 단층손상대의 유형(tip-, relay-, splay) 별 위상기하를 분석하여 각 유형의 연결성과 배열을 정량화 하였다(Fig. 9). 말단(tip-)손상대는 I-노드와 II-, IC-브랜치의 비율이 큰 위상기하학적 특징을 보이며, 브랜치 당 평균 연결 개수(C_B)가 적었다. 이와 달리 연결(relay-), 분기(splay-)손상대에서는 Y-노드와 CC-브랜치의 비율이 크고 C_B가 큰 값을 가지는 잘 연결된 단층계의 위상기하학적 특성을 보였다. 이들은 단층이 전파되고, 서로 상호작용하고, 서로 연결되어 성숙도가 높아지면서 위상기하가 어떻게 변하는지를 제시하였다. I-노드와 II-브랜치가 많은 네트워크에서 성숙해질수록 Y-노드와 CC-브랜치가 많은 네트워크로 진화해 결과적으로 연결성이 더 높아진다는 결론을 내렸다. 또한 평면에서 얻을 수 있는 말단(tip-), 연결(relay-)손상대에 대한 정보와 단면에서 얻을 수 있는 분기(splay-)손상대에 대한 정보를 통합하여 단층손상대의 3차원 위상기하와 연결성 분석에 대한 가능성을 제시하였다. 그들은 단층손상대의 위상기하학적 진화정도가 유체유동에 중요하게 적용된다는 점을 강조했다.

https://static.apub.kr/journalsite/sites/kseg/2021-031-01/N0520310101/images/kseg_31_01_01_F9.jpg

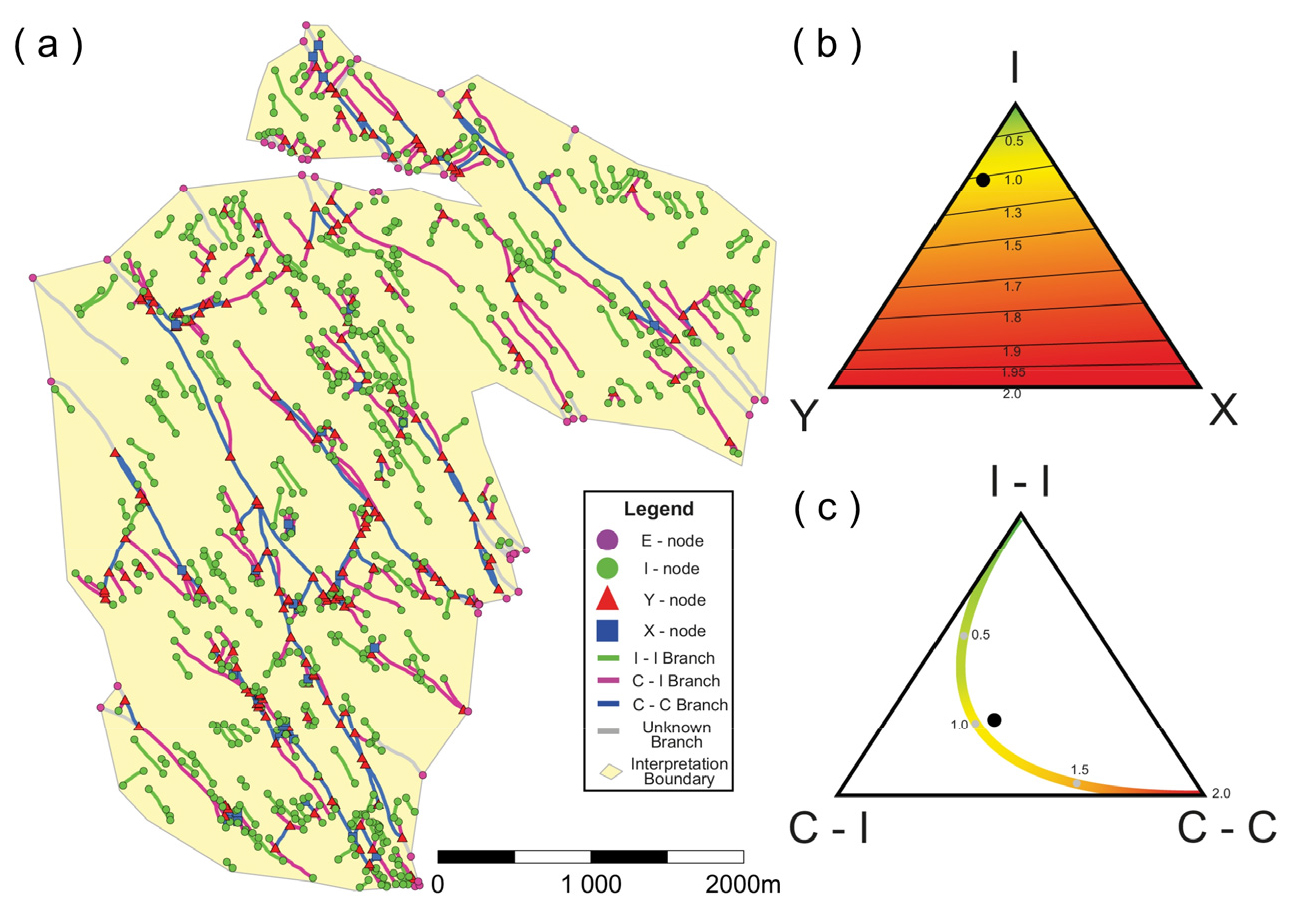
Fig. 9

Branch triangular plots of fault tip damage zone; (a) relay damage zone, (b) and splay damage zone; (c) study area of Nixon et al. (2020). The red arrows represent the direction of evolution into a more complex fracture network (from Nixon et al., 2020).

프로그램을 이용한 단열계의 위상기하학 분석

단열계의 2차원 패턴 정량화는 단열계 형성의 기원이 되는 메커니즘을 이해하고, 지하에서의 단열계 크기와 확장범위에 대한 추정에 도움이 되며, 이들을 바탕으로 단열계가 발달한 암체의 연결성과 투수성 같은 특성에 대한 정보를 얻을 수 있다(Healy et al., 2017). 단열계의 2차원 패턴을 정량화 할 때 여러 가지 프로그램이 이용되는데, 여기서는 그 중 MATLAB^TM과 ArcGIS^TM를 이용한 위상기하 분석에 대해서 간략하게 소개하고자 한다.

먼저 MATLAB^TM은 FracPaQ라는 툴박스를 이용하여 분석을 실시한다(Healy et al., 2017). 이용되는 입력 데이터로는 .JPG(.JPEG) 혹은 .TIF(.TIFF)같은 이미지 파일이나, .SVG 같은 노드 파일을 이용한다. 이 툴박스를 실행하면 단열 개별의 특성(길이, 방향)과 단열계 전체의 특성(연결성, 투수성)에 대한 정량적 분석을 도시화하는 트래이스 맵과 도표들이 출력된다(Fig. 10).

https://static.apub.kr/journalsite/sites/kseg/2021-031-01/N0520310101/images/kseg_31_01_01_F10.jpg

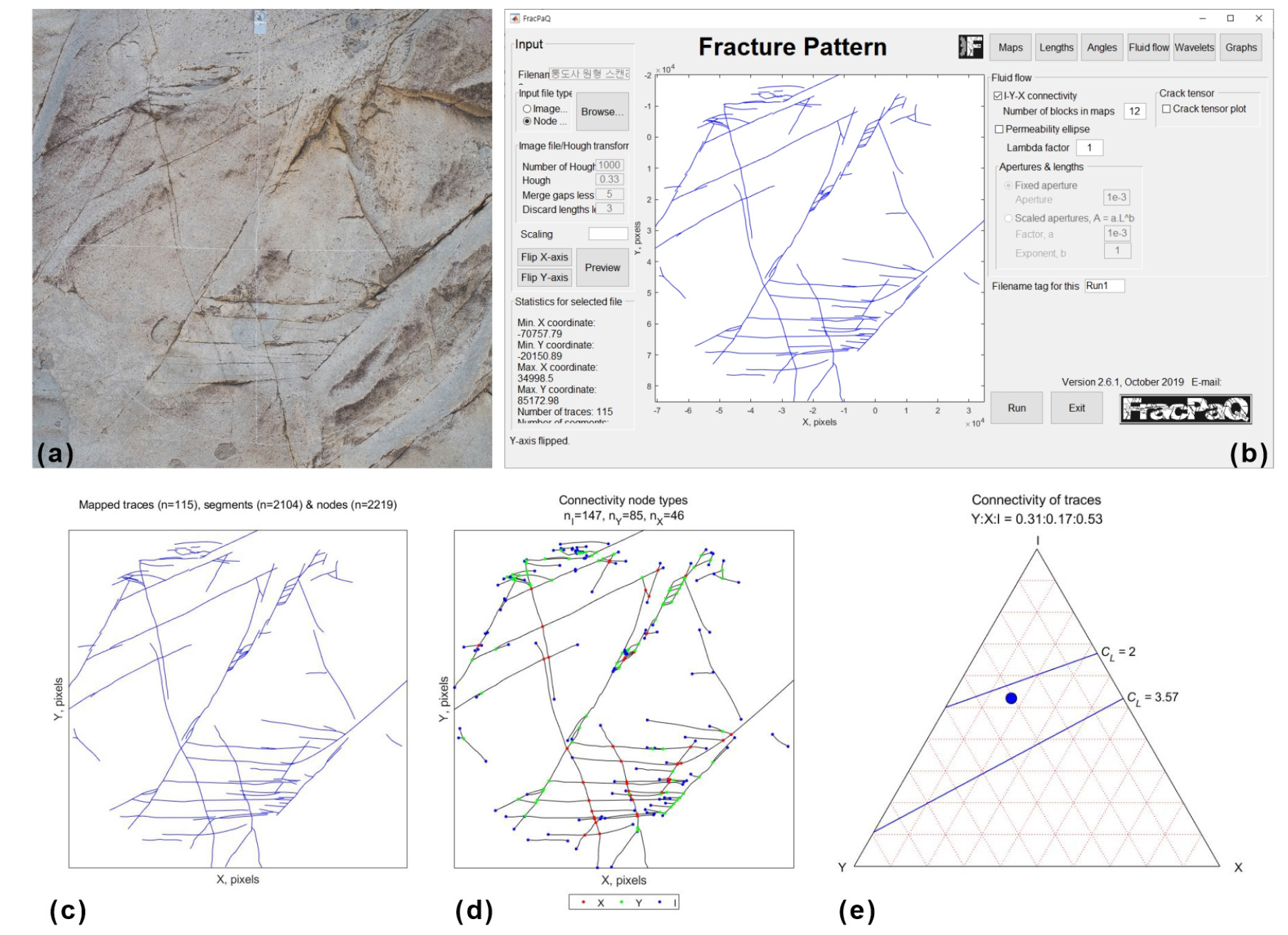
Fig. 10

Example use of FracPaQ: a MATLAB^TM toolbox for topological analysis of fracture networks. (a) Outcrop photograph of a fractured plane at Tongdosa, Yangsan, Korea. (b) Screenshot of FracPaQ in use on a Windows computer. (c) Trace map of (a). (d) Trace map with topology characteristics. (e) Triangular plot of (a).

ArcGIS^TM는 NetworkGT라는 툴박스를 이용하여 분석을 실시한다(Nyberg et al., 2018). 디지털화된 이미지를 입력하여 툴박스를 실행하면, 단열밀도에 대한 장미도, 위상기하에 관한 도표, 위상기하학적 매핑을 출력 할 수 있다(Fig. 11).

https://static.apub.kr/journalsite/sites/kseg/2021-031-01/N0520310101/images/kseg_31_01_01_F11.jpg

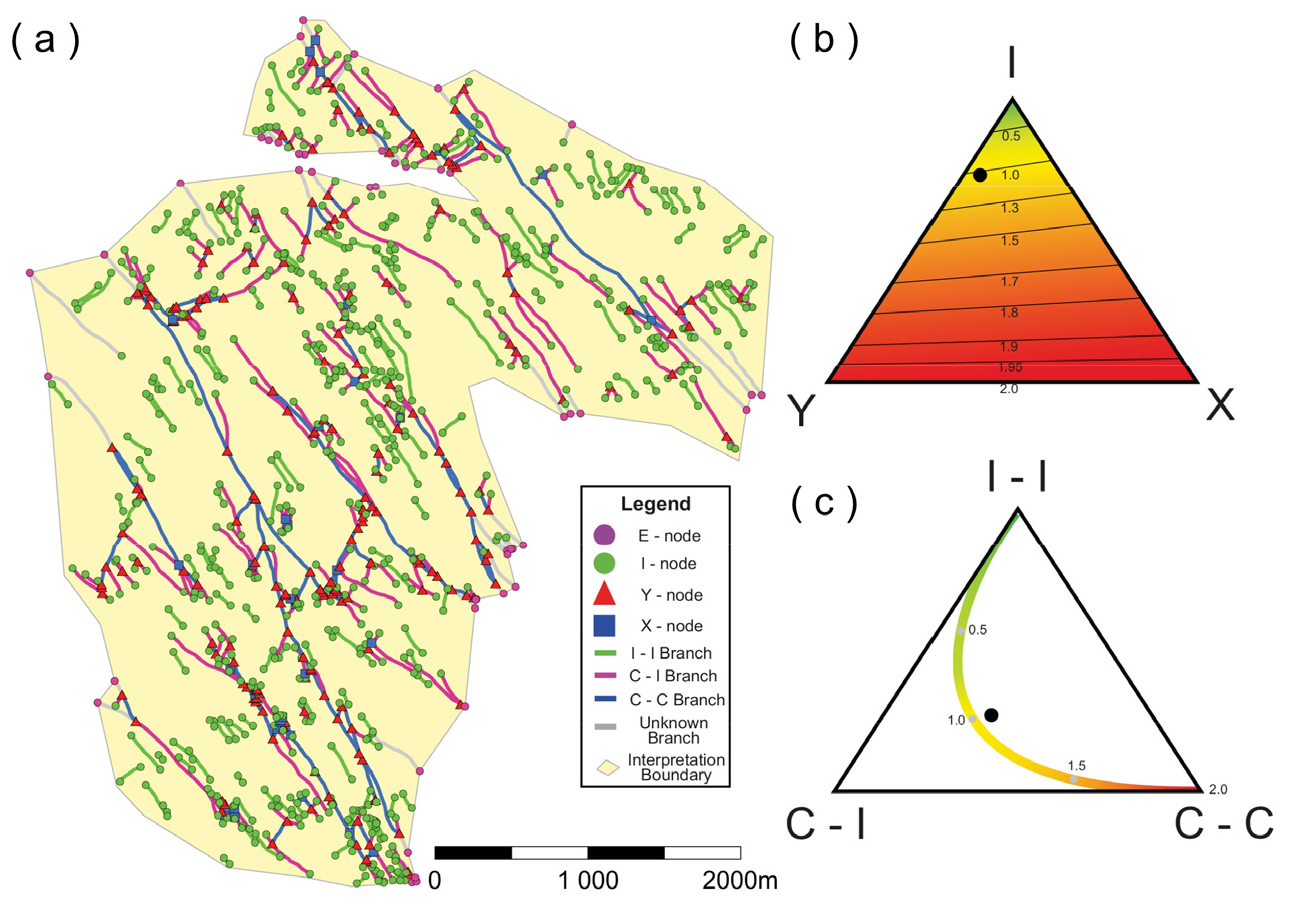
Fig. 11

Example use of NetworkGT: a GIS toolbox for geometric and topological analysis of fracture networks. (a) Trace map with topological characteristics of a fractured offshore locality in NW Devon, UK. (b) Triangular plot of nodes in (a). (c) Triangular plots of branches in (a) (from Nyberg et al., 2018).

토 의

일반적으로, 단열계 연구에 이용되는 데이터는 지표에 드러난 2차원의 단열계 자취로부터 획득한다. 하지만 단열계는 암체 내에 발달하는 3차원 구조로, 단열계의 정확한 연결성 분석을 하기 위해서는 3차원 분석이 이뤄져야 한다. 또한 단열 강도(밀도)는 단열이 발달하는 층의 두께, 암석, 지체구조적 환경 등 여러 요인의 영향을 받는다고 알려져 있다. 단열계의 위상기하와 단열강도(밀도)가 밀접하게 연관되어 있기 때문에 결국 단열강도(밀도)를 결정하는 요소들이 단열계의 위상기하에 영향을 미칠 것이다. 따라서 이 장에서는 단열계의 3차원 위상기하분석과 위상기하에 영향을 미치는 요인에 대해서 토의하려 한다.

단열계의 3차원 위상기하 분석

Sanderson and Nixon(2015)은 시추공 영상검층을 이용하여 단열계의 3차원적 위상기하 분석 가능성을 논의하였다. 대부분 단열계의 길이규모는 시추공 지름의 길이규모보다 크기 때문에 시추공 영상검층으로 단열계 전체의 정보를 얻는 것은 어려운 실정이다. 하지만 그들은 영상검층에서 획득한 단열계 일부의 위상기하학적 특성으로 단열계 전체의 특성을 추측하는 가능성을 제시하였다. Fig. 12의 시추공 영상검층에서, 단열의 말단은 I-노드(초록)로, 단열이 교차하는 곳을 X-노드(파랑)로, 다른 단열에 붙거나 분기하는 곳을 Y-노드(빨강)로 표시하였다. Fig. 12d는 영상검층에서 획득된 각 노드의 비율을 노드삼각도표에 도시한 것이다.

https://static.apub.kr/journalsite/sites/kseg/2021-031-01/N0520310101/images/kseg_31_01_01_F12.jpg

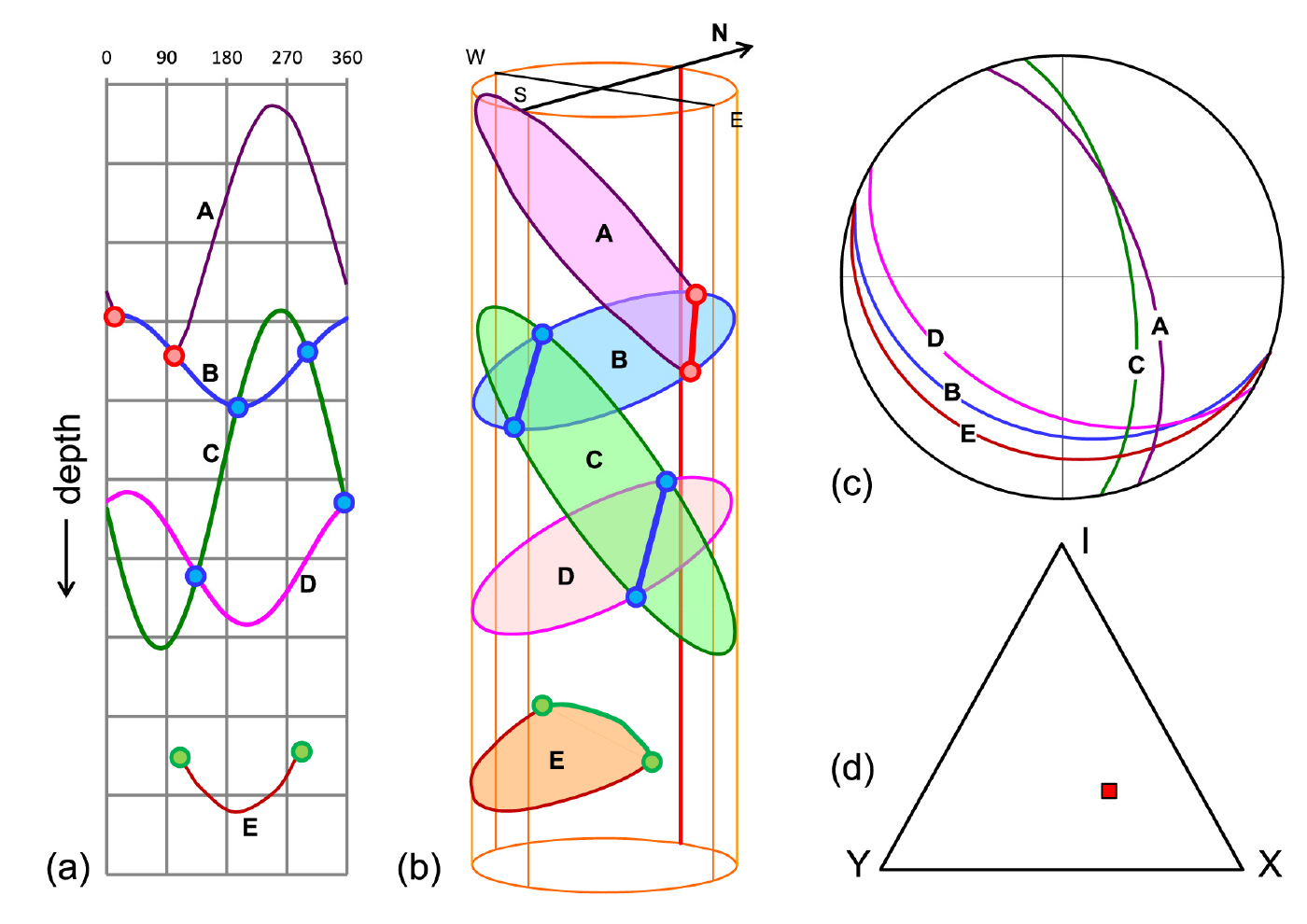
Fig. 12

Example of three-dimensional topology analysis of fracture network using borehole image log data. (a) Borehole image log of fracture network consisting of nodes and branches. (b) Three-dimensional borehole with fracture network. (c) Stereogram of (a). (d) Triangular plot of (a) (from Sanderson and Nixon, 2015).

Sanderson et al.(2019)은 단열계의 3차원 위상기하 분석에 대한 추가 연구에서, 단층계의 탄성파탐사체(seismic volume)와 단열계의 단층촬영(CT scanning)으로부터 3차원 위상기하학적 분석의 가능성을 논의하였다. 이들은 단열계(또는 단층계)의 정육면체 샘플을 이용해 이론적인 단열계의 3차원 위상기하분석방법을 제시하였다. 기존 단열계의 2차원 분석에서 브랜치와 단열선은 면으로, 노드는 선으로, 그리고 단열계에 의해 만들어진 블록(다각형의 영역)은 다면체로 표현될 것이다. 정육면체의 윗변은 2차원 분석에서 시행되는 트레이스 맵이고, 두 옆면은 단면을 나타낸다. 서로 다른 위상기하를 가지는 세 면의 매개변수 평균을 구해 해당 단열계의 3차원 위상기하를 분석하는 방법을 제시하였다(Fig. 13e). 또한 단열의 브랜치면 경사를 이용해 브랜치면이 샘플면과 만나는 확률과 노드선 선경사를 이용해 노드선이 샘플면과 만나는 확률을 구해 3차원 위상기하의 추정값을 구할 수 있음을 보여주었다(Fig. 13b). 하지만 이에 대해서는 아직 추가적인 연구가 더 필요한 실정이다.

https://static.apub.kr/journalsite/sites/kseg/2021-031-01/N0520310101/images/kseg_31_01_01_F13.jpg

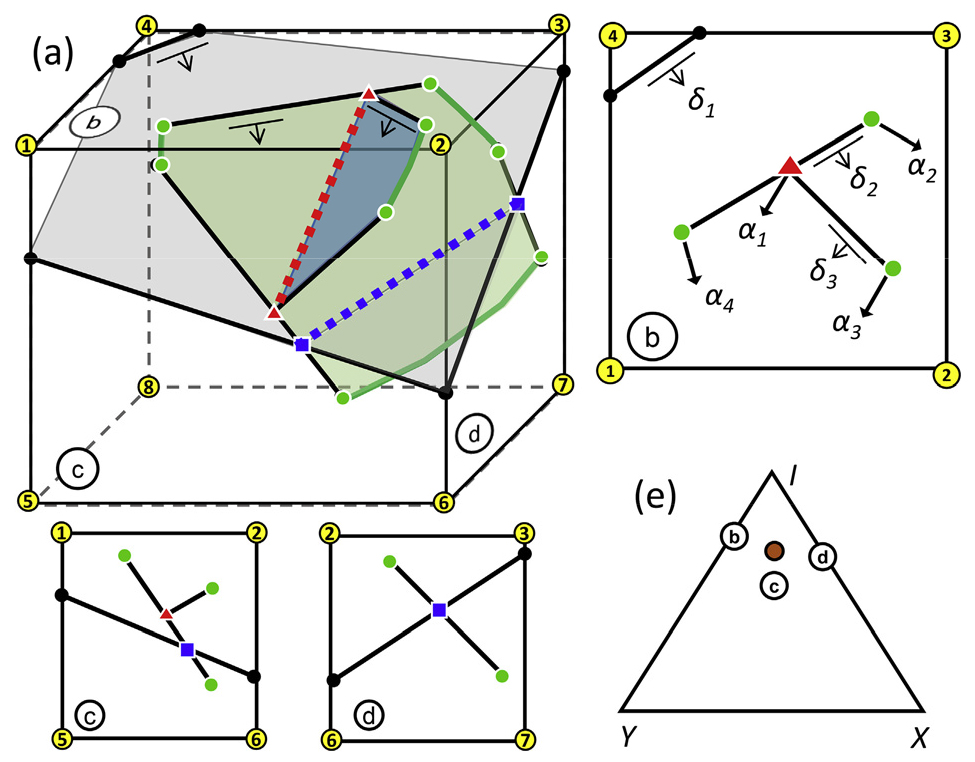
Fig. 13

(a) Projection of the fracture network within a cube. (b) Top surface of (a) with plunges of lines and dips of fractures. (c) And (d) are two side sections of (a). (e) Triangular plots of each surface of (a) and average value of them (from Sanderson et al., 2019).

단열계의 위상기하에 영향을 미치는 요인

단열계의 위상기하학적 분석이 단열계의 특성화에 유용하다는 것은 인정되고 있지만 최근에 이러한 연구들이 시작되었기 때문에 아직은 분석에서의 많은 문제점들이 제대로 논의되지 못하고 있다. 특히 단열계의 위상기하에 영향을 미치는 요인들을 분석하고 해석하는데 있어서는 매우 많고 복잡한 제어요소들이 단열계의 형성에 관여하고 있기 때문에 아직도 이들에 대한 이해가 많이 부족한 실정이다. 단열계의 위상기하를 제어하는 요소들에는 층의 두께와 단열강도, 석회암의 백운암화, 단층이 존재하는 암체의 지체구조적 변형사 등이 있다.

기존에는 단열이 발달하는 층의 두께(bed thickness)와 단열강도 사이는 반비례관계라고 알려져 왔지만(Ladeira and Price, 1981; Pollard and Aydin, 1988; Huang and Angelier, 1989; Narr and Suppe, 1991), Procter and Sanderson(2018)의 연구에서는 층의 두께와 단열강도 사이의 연관성이 보이지 않았고, 심지어 다른 연구(Wennberg et al., 2006; Ortega et al., 2010)에서는 층 두께와 단열 강도가 비례한다는 결론을 지었다. 따라서 이런 문제들을 해결하기 위해서는 층 두께와 단열강도(밀도), 그리고 단열계의 위상기하 사이의 관계에 대한 추가적인 연구들이 더욱 많이 이뤄져야 한다.

Nixon et al.(2020)의 연구에서는 석회암의 입자크기와 이암의 조성차이로 인한 다양한 단층손상대 양상을 확인 할 수 있었고, 결국 이들이 단층손상대의 위상기하에 영향을 미치기 때문에 단층손상대를 특성화 하는데 위상기하를 이용해야 한다고 주장하고 있다. 또한 여러 연구자들(Rustichelli et al., 2015; Giorgioni et al., 2016; Korneva er al., 2018)에 의해 석회암의 백운암화 정도가 단열밀도와 단열간격에 영향을 미친다고 보고되었다. 이들의 연구결과를 바탕으로 석회암의 백운암화 정도가 단열계의 위상기하에 영향을 미칠 수 있음을 고려 할 수 있지만 이에 대해서도 더욱 정량적인 분석을 통한 추가적인 연구가 더 필요한 실정이다.

또한 Duffy et al.(2017)은 지체구조적 변형사에 따른 정단층의 위상기하 발달과정을 보여주었다. 한 방향으로 응력이 작용했을 경우 비교적 간단한 위상기하를 가지는 단층계를 형성하는 반면, 두 방향으로 응력이 작용했을 경우에는 비교적 복잡한 위상기하를 가지는 단층계가 형성되는 것을 확인하였다. 이를 바탕으로 단층계를 특성화 하는데 위상기하를 이용하는 것이 유용하다고 주장하고 있다. 따라서 앞으로 이러한 단열계에 대한 위상기하학의 적용은 좀 더 발전된다면 단열계의 진화와 유체의 유동특성뿐만 아니라 방사성폐기물처분장과 같은 주요 시설물의 부지선정과 활성단층을 분석하여 미래의 단층파열 가능성을 예측하는 분야에까지도 적용이 가능할 수 있을 것으로 판단된다.

결 론

본 연구에서는 단열계를 특성화 할 때, 단열계의 위상기하를 분석하여 특성화하는 방법에 대하여 간략히 소개하고, 단열계 위상기하 분석의 연구동향을 고찰해 보았다. 기존의 단순 밀도분석이나 기하학적 분석만으로는 단열계의 연결성과 같은 단열 간 공간적 관계에 대한 정량적 정보를 얻기 힘들기 때문에 위상기하학적 분석도 같이 시행하여 단열계를 특성화 해야 한다. 단열계의 위상기하학적 분석으로 단열계의 연결성과 밀집성을 나타내는 매개변수를 구하는 방법과 단열계를 그래프이론에 적용해 연결성을 나타내는 매개변수를 구하는 방법을 소개하였다. 또한 위상기하학을 이용한 단열계 특성분석의 최근 연구동향, 단열계의 3차원적 위상기하분석 그리고 단열계 위상기하에 영향을 미칠 수 있는 요소에 대해 토의하였다. 위상기하 분석법으로 단열계의 연결성과 풍부성을 정량화하여 단열계가 발달하는 암체의 투수성을 설명할 수 있어 지하수 유동 특성을 이해하는데 도움이 될 수 있고, 방사성폐기물처분장과 같은 주요 시설물의 부지선정과 안정성을 평가하는 데에도 도움이 될 수 있다. 또한 위상기하 분석은 단열배열의 발달특성 연구에도 도움이 될 수 있다. 본 연구 결과를 아래와 같이 정리하였다.

(1) 2차원에서 단열계의 위상기하는 단열선(lines), 노드(nodes), 브랜치(branches)로 이뤄진 네트워크로 설명된다. 이들의 개수를 수학적으로 조합하여 단열계의 연결성을 나타내는 매개변수(N_B/N_L, C_L, C_B)와 밀집성을 나타내는 매개변수(B₂₀, B₂₁, B₂₂)를 구할 수 있다.

(2) 단열계를 그래프이론에 적용한다면 한 단열계는 노드(꼭짓점)와 브랜치(빗변)로 이뤄진 평면 그래프로 간주 할 수 있다. 이들의 개수를 이용하여 단열계의 연결성을 나타내는 매개변수(<d>)를 구할 수 있다. 또한 오일러 공식을 이용하여 노드, 브랜치, 영역, 연결요소의 관계를 나타내는 방정식을 얻을 수 있다.

(3) 최근까지 단열계의 위상기하 분석을 이용한 다양한 연구가 이뤄져 왔으며, 앞으로 더 많은 활용이 가능할 것이다. 현재까지는 주로 단층손상대의 각 유형별 연결성과 배열을 정량화하는 연구, 구조적 복잡성과 지하수 유동 사이의 관계에 대한 연구 등 다양한 단열 연구에 단열계의 위상기하 분석으로 얻은 연결성에 대한 데이터가 이용되었다.

(4) 아직은 더 많은 연구가 필요하지만 여러 연구자들에 의해 단열계의 3차원 위상기하 분석에도 다양한 이론적 접근이 이뤄져 왔다. 또한 단열밀도에 영향을 미치는 여러 요인들이 단열계의 위상기하에도 영향을 미칠 것으로 생각되어 연구되고 있으며, 이에 대해서는 앞으로 더 많은 추가적인 연구가 필요해 보인다.

Acknowledgements

이 논문은 부경대학교 자율창의학술연구비(2019년)에 의하여 연구되었음.

References

Adler, P.M., Thovert, J.F., 1999, Fractures and fracture networks, Kluwer Academic Publishers, 431p. 10.1007/978-94-017-1599-7

Balberg, I., Anderson, C.H., Alexander, S., Wagner, N., 1984, Excluded volume and its relation to the onset of percolation, Physical Review B, 30(7), 3933-3943. 10.1103/PhysRevB.30.3933

Berkowitz, B., Balberg, I., 1993, Percolation theory and its application to groundwater hydrology, Water Resources Research, 29(4), 775-794. 10.1029/92WR02707

Bisdom, K., Gauthier, B.D.M., Bertotti, G., Hardebol, N.J., 2014, Calibrating discrete fracture-network models with a carbonate three-dimensional outcrop fracture network: implications for naturally fractured reservoir modeling, American Association of Petroleum Geologists Bulletin, 98(7), 1351-1376. 10.1306/02031413060

Clarke, B.A., Burbank, D.W., 2011, Quantifying bedrock-fracture patterns within the shallow subsurface: implications for rock mass strength, bedrock landslides, and erodibility, Journal of Geophysical Research, 116(F4), F04009. 10.1029/2011JF001987

Dimmen, V., Rotevatn, A., Peacock, D.C.P., Nixon, C.W., Nærland, K., 2017, Quantifying structural controls on fluid flow: insights from carbonate-hosted fault damage zones on the Maltese Islands, Journal of Structural Geology, 101, 43-57. 10.1016/j.jsg.2017.05.012

Duffy, O.B., Nixon, C.W., Bell, R.E., Jackson, C.A.L., Gawthorpe, R.L., Sanderson, D.J., Whipp, P.S., 2017, The topology of evolving rift fault networks: single-phase vs multi-phase rifts, Journal of Structural Geology, 96, 192-202. 10.1016/j.jsg.2017.02.001

Euler, L., 1758, Elementa doctrinae solidorum, Novi Commentarii Academiae Scientiarum Petropolitanae, 4, 109-140.

Giorgioni, M., Iannace, A., D'Amore, M., Dati, F., Galluccio, L., Guerriero, V., Mazzoli, S., Parente, M., Strauss, C., Vitale, S., 2016, Impact of early dolomitization on multi-scale petrophysical heterogeneities and fracture intensity of low-porosity platform carbonates (Albian-Cenomanian, southern Apennines, Italy), Marine and Petroleum Geology, 73, 462-478. 10.1016/j.marpetgeo.2016.03.011

Healy, D., Rizzo, R.E., Cornwell, D.G., Farrell, N.J.C., Watkins, H., Timms, N.E., Gomez-Rivas, E., Smith, M., 2017, FracPaQ: a MATLAB^TM toolbox for the quantification of fracture patterns, Journal of Structural Geology, 95, 1-16. 10.1016/j.jsg.2016.12.003

Huang, Q., Angelier, J., 1989, Fracture spacing and its relation to bed thickness, Geological Magazine, 126(4), 355-362. 10.1017/S0016756800006555

Jing, L., Stephansson, O., 1997, Network topology and homogenization of fractured rocks, In: Jamtveit, B., Yardley, B.W. (Eds.), Fluid Flow and Transport in Rocks: Mechanisms and Effects, Chapman & Hall, 191-202. 10.1007/978-94-009-1533-6_11

Jolley, S.J., Barr, D., Walsh, J.J., Knipe, R.J., 2007, Structurally complex reservoirs: an introduction, Geological Society Special Publication, 292, 1-24. 10.1144/SP292.1

Korneva, I., Bastesen, E., Corlett, H., Eker, A., Hirani, J., Hollis, C., Gawthorpe, R.L., Rotevatn, A., Taylor, R., 2018, The effects of dolomitization on petrophysical properties and fracture distribution within rift-related carbonates (Hammam Faraun Fault Block, Suez Rift, Egypt), Journal of Structural Geology, 108, 108-120. 10.1016/j.jsg.2017.06.005

Krabbendam, M., Glasser, N.F., 2011, Glacial erosion and bedrock properties in NW Scotland: abrasion and plucking, hardness and joint spacing, Geomorphology, 130(3-4), 374-383. 10.1016/j.geomorph.2011.04.022

Ladeira, F.L., Price, N.J., 1981, Relationship between fracture spacing and bed thickness, Journal of Structural Geology, 3(2), 179-183. 10.1016/0191-8141(81)90013-4

Laubach, S.E., Lamarche, J., Gauthier, B.D.M., Dunne, W.M., Sanderson, D.J., 2018, Spatial arrangement of faults and opening-mode fractures, Journal of Structural Geology, 108, 2-15. 10.1016/j.jsg.2017.08.008

Manzocchi, T., 2002, The connectivity of two-dimensional networks of spatially correlated fractures, Water Resources Research, 38(9), 1162. 10.1029/2000WR000180

Morley, C.K., Nixon, C.W., 2016, Topological characteristics of simple and complex normal fault networks, Journal of Structural Geology, 84, 68-84. 10.1016/j.jsg.2016.01.005

Narr, W., Suppe, J., 1991, Joint spacing in sedimentary rocks, Journal of Structural Geology, 13(9), 1037-1048. 10.1016/0191-8141(91)90055-N

Nixon, C.W., Nærland, K., Rotevatn, A., Dimmen, V., Sanderson, D.J., Kristensen, T.B., 2020, Connectivity and network development of carbonate-hosted fault damage zones from western Malta, Journal of Structural Geology, 141, 104212. 10.1016/j.jsg.2020.104212

Nyberg, B., Nixon, C.W., Sanderson, D.J., 2018, NetworkGT: a GIS tool for geometric and topological analysis of two-dimensional fracture networks, Geosphere, 14(4), 1618-1634. 10.1130/GES01595.1

Odling, N., Gillespie, P., Bourgine, B., Castaing, C., Chiles, J., Christensen, N., Fillion, E., Genter, A., Olsen, C., Thrane, L., 1999, Variations in fracture system geometry and their implications for fluid flow in fractures hydrocarbon reservoirs, Petroleum Geoscience, 5(4), 373-384. 10.1144/petgeo.5.4.373

Ortega, O.J., Gale, J.F.W., Marrett, R., 2010, Quantifying diagenetic and stratigraphic controls on fracture intensity in platform carbonates: an example from the Sierra Madre Oriental, northeast Mexico, Journal of Structural Geology, 32(12), 1943-1959. 10.1016/j.jsg.2010.07.004

Pérez-Flores, P., Veloso, E., Cembrano, J., Sánchez-Alfaro, P., Lizama, M., Arancibia, G., 2017, Fracture network, fluid pathways and paleostress at the Tolhuaca geothermal field, Journal of Structural Geology, 96, 134-148. 10.1016/j.jsg.2017.01.009

Pollard, D.D., Aydin, A., 1988, Progress in understanding jointing over the past century, Geological Society of America Bulletin, 100(8), 1181-1204. 10.1130/0016-7606(1988)100<1181:PIUJOT>2.3.CO;2

Procter, A., Sanderson, D.J., 2018, Spatial and layer-controlled variability in fracture networks, Journal of Structural Geology, 108, 52-65. 10.1016/j.jsg.2017.07.008

Rustichelli, A., Iannace, A., Girundo, M., 2015, Dolomitization impact on fracture density in pelagic carbonates: contrasting case studies from the Gargano Promontory and the Southern Apennines (Italy), Italian Journal of Geosciences, 134(3), 556-575. 10.3301/IJG.2014.43

Sanderson, D.J., Nixon, C.W., 2015, The use of topology in fracture network characterization, Journal of Structural Geology, 72, 55-66. 10.1016/j.jsg.2015.01.005

Sanderson, D.J., Nixon, C.W., 2018, Topology, connectivity and percolation in fracture networks, Journal of Structural Geology, 115, 167-177. 10.1016/j.jsg.2018.07.011

Sanderson, D.J., Peacock, D.C.P., Nixon, C.W., Rotevatn, A., 2019, Graph theory and the analysis of fracture networks, Journal of Structural Geology, 125, 155-165. 10.1016/j.jsg.2018.04.011

Singhal, B.B.S., Gupta, R.P., 2010, Applied hydrogeology of fractured rocks, Springer Science and Business Media, 408p. 10.1007/978-90-481-8799-7

Son, H., Kim, Y.S., 2020, Potential applications of fracture characterization based on topology, Poster session presented at the 2020 Fall Joint Conference of the Geological Sciences, Korea.

Wennberg, O.P., Svånå, T., Azizzadeh, M., Aqrawi, A.M.M., Brockbank, P., Lyslo, K.B., Ogilvie, S., 2006, Fracture intensity vs. mechanical stratigraphy in platform top carbonates: the Aquitanian of the Asmari Formation, Khaviz Anticline, Zagros, SW Iran, Petroleum Geoscience, 12(3), 235-246. 10.1144/1354-079305-675

The Journal of Engineering Geology ISSN:1226-5268(Print) 2287-7169(Online) 지질공학

Preview

Review of Quantification of Fracture Characteristics Based on Topological Analysis

ABSTRACT

MAIN

Fig. 1

Terminology of node and branch model (modified from Nyberg et al., 2018). (b) The triangular plot of a relative number of nodes in (a) (after Manzocchi, 2002).

(1)

(2)

(3)

(4)

Fig. 2

Triangular plots of a relative number of nodes. (a) Ratio of the number of branches to lines (NB/NL). (b) Average number of connections per line (CL) (modified from Sanderson and Nixon, 2015). The value of 3.57 means that the fracture network is well connected.

(5)

(6)

(7)

(8)

Fig. 3

(a) Triangular plots of the relative number of each branch type with average number of connections per branch (CB). (b) Triangular plots of the relative number of nodes with average number of connections per branch (CB) (modified from Sanderson and Nixon, 2015).

(9)

(10)

(11)

Fig. 4

Examples of a directed graph (a), an undirected graph (b), and a directed graph with a loop and a multi branch (c).

Fig. 5

Examples of traversing adjacent nodes. (a) Walk (ABCDBD), (b) trail (ABCDB), (c) path (ABCDEF), and (d) cycle (ABCDEFA).

Fig. 6

(a) Trace map of fracture network with three connected components (i–iii). (b) Node and branch model of (a), notation as in Fig. 1a. (c) Graph features (node, branch, connected components, regions) of (a) (modified from Sanderson et al., 2019).

(12)

Fig. 7

Triangular plots of nodes with average degree of nodes (<d>) and examples of fracture networks showing the different average degree of nodes (<d>) (modified from Sanderson et al., 2019).

(13)

(14)

(15)

Fig. 8

Fig. 9

Branch triangular plots of fault tip damage zone; (a) relay damage zone, (b) and splay damage zone; (c) study area of Nixon et al. (2020). The red arrows represent the direction of evolution into a more complex fracture network (from Nixon et al., 2020).

Fig. 10

Fig. 11

Fig. 12

Fig. 13

(a) Projection of the fracture network within a cube. (b) Top surface of (a) with plunges of lines and dips of fractures. (c) And (d) are two side sections of (a). (e) Triangular plots of each surface of (a) and average value of them (from Sanderson et al., 2019).

Acknowledgements

References

Triangular plots of a relative number of nodes. (a) Ratio of the number of branches to lines (N_B/N_L). (b) Average number of connections per line (C_L) (modified from Sanderson and Nixon, 2015). The value of 3.57 means that the fracture network is well connected.

(a) Triangular plots of the relative number of each branch type with average number of connections per branch (C_B). (b) Triangular plots of the relative number of nodes with average number of connections per branch (C_B) (modified from Sanderson and Nixon, 2015).