A Closed-Form Solution for Circular Openings in an Elastic–Brittle–Plastic Extended Spatial Mobilized Plane Medium

Chuangzhou Wu; Wei Guo; Bo-An Jang

doi:10.9720/kseg.2022.1.001

Preview

Research Article

The Journal of Engineering Geology. 31 March 2022. 1-12
https://doi.org/10.9720/kseg.2022.1.001

A Closed-Form Solution for Circular Openings in an Elastic–Brittle–Plastic Extended Spatial Mobilized Plane Medium

Chuangzhou Wu¹

Wei Guo²

Bo-An Jang³^*

¹Professor, Institute of Port, Coastal and Offshore Engineering, Ocean College, Zhejiang University

²Professor, State Key Laboratory of Hydraulic Engineering Simulation and Safety, School of Civil Engineering, Tianjin University

³Professor, Department of Geophysics, Kangwon National University

^{*Corresponding Author}

ABSTRACT

Based on the extended spatial mobilization plane (SMP) criterion, we present an elastic-brittle-plastic solution for an axisymmetric cylindrical tunnel. The influences of the intermediate principal compressive stress and material strain-softening behavior are considered. Closed-form formulas for the critical support force, radius of plastic zone, and distributions of stress and displacement in surrounding rock are proposed. The elastic-plastic solution based on SMP is compared with the Kastner solution to verify the credibility of the obtained elastic-plastic solution. The elastic-brittle-plastic solution following the SMP criterion and the current solution based on the Mohr-Coulomb criterion are also compared. The rock strain-softening rate and the intermediate principal stress affect the stability of the surrounding rock. The results provide guidance for optimizing the design of support systems for tunnels.

Keywords

tunnel

underground construction

rock

failure

tunneling

plasticity

MAIN

Introduction
Model Description
Problem Definition
Analytical Solution for Stresses and Displacement in the Plastic Region
Comparison of Solutions
Perfect-Plastic Medium
Elastic-Brittle-Plastic Medium
Conclusions

Introduction

Symmetrical circular tunnels are widely considered in geotechnical engineering, and many closed-form solutions and numerical methods have been developed for design of their support systems (Detournay, 1986; Wang, 1996; Carranza-Torres and Fairhurst, 1999; Egger, 2000; Alonso et al., 2003; Wang et al., 2010; Osman and Randolph, 2011; Zareifard and Fahimifar, 2014; Fahimifar et al., 2015; Zhao et al., 2016; Katebian and Molladavoodi, 2017). Many studies have focused on analytical solutions for a circular underground opening in brittle-plastic rock mass governed by the linear Mohr-Coulomb (M-C) and the nonlinear Hoek-Brown (H-B) failure criteria. Brown et al. (1983) reviewed previous work, and developed a closed-form solution for an elastic-brittle-plastic H-B medium and a numerical solution for a strain-softening H-B medium. Ogawa and Lo (1987) derived an analytical solution and analyzed the effects of dilatancy and yield criteria on the displacement and stress around tunnels. Sharan (2003, 2005) presented closed-form solutions for elastic-brittle-plastic H-B rock. Park and Kim (2006) derived a closed-form solution for a circular tunnel in a brittle-plastic rock mass governed by the H-B yield criterion, and compared the displacement in the plastic zone under different elastic strain conditions.

However, these previous solutions consider 2D failure criteria, which neglect the effect of the intermediate principal stress ( $σ_{2}$ ) on the strength parameter and displacement of the surrounding rocks under excavation. To address these issues, this work considers the effect of the intermediate principal stress for an elastic-brittle-plastic medium. The extended spatially mobilized plane (SMP) is employed for frictional and cohesive materials in 3D stress space (termed ‘extended SMP’) (Nakai and Matsuoka, 1983; Matsuoka and Sun, 1995). This paper presents an analytical solution for circular tunnel excavation in brittle-plastic M-C and extended SMP media considering the effect of the intermediate principal stress. The solution was transformed from brittle-plastic solutions to perfect-plastic solutions when setting the residual strength parameters equal to the peak values. Comparison of the displacements and stresses of the solutions with the Kastner solution indicates that brittle-plastic behavior of rock mass greatly extends the plastic zone and the displacements around the cavity due to the effect of the intermediate principal stress. Ground response curves are produced for both M-C and extended SMP criteria, and the effects of the intermediate principal stress on cavity wall convergence and the plastic radius are discussed.

Model Description

Problem Definition

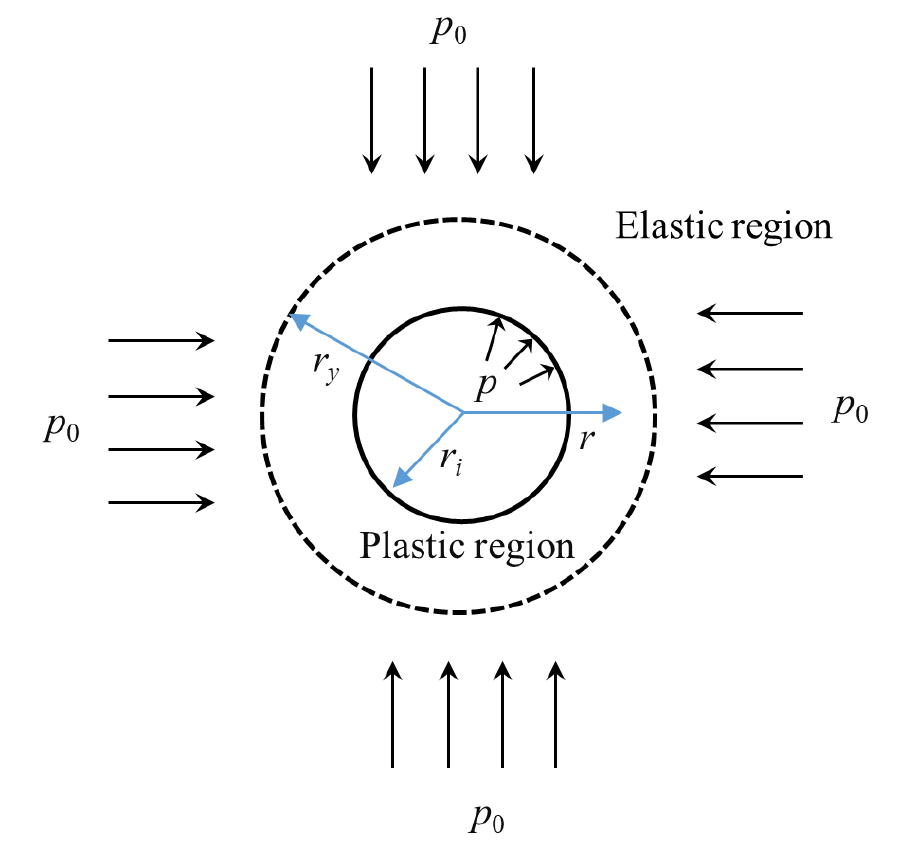
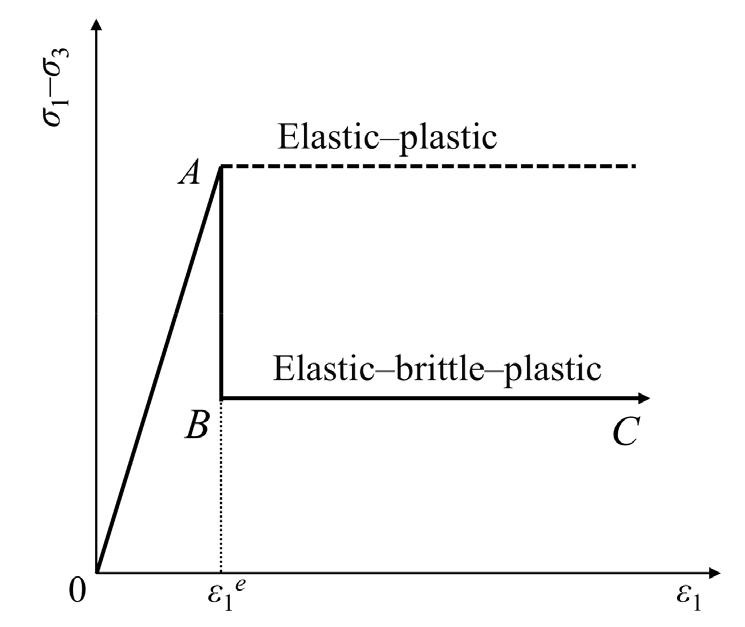
Fig. 1 shows a circular tunnel being excavated in an initially elastic rock mass subjected to a hydrostatic stress $p_{0}$ . The tunnel surface is subjected to an internal pressure $p$ . A plastic region develops around the opening when p reaches the yield stress. Upon yielding, the rock’s strength suddenly drops, and it then follows post-yield mechanical behavior as shown in Fig. 2. The H-B and M-C criteria are the most commonly used strength criteria for rock masses, both of which neglect the effect of the intermediate principal stress on the stress and displacement of the elastic and plastic regions. The extended SMP failure criterion, which considers the effect of the intermediate principal stress $σ_{2}$ , is adopted here to solve the stresses and displacements in the plastic region.

https://static.apub.kr/journalsite/sites/kseg/2022-032-01/N0520320101/images/kseg_32_01_01_F1.jpg

Fig. 1.

A circular opening in an infinite medium. $r_{i}$ and $r_{y}$ are the radii of the tunnel and plastic region, respectively. $p$ is the internal pressure and $p_{0}$ is the hydrostatic stress of the rock mass.

https://static.apub.kr/journalsite/sites/kseg/2022-032-01/N0520320101/images/kseg_32_01_01_F2.jpg

Fig. 2.

Relationship between stress and strain for an elastic-brittle-plastic medium.

The extension of SMP for cohesive and frictional materials by Matsuoka and Sun (1995) and Nakai and Matsuoka (1983) defined the extended SMP failure criterion as follows:

(1)

\frac{{\hat{τ}}_{S M P}}{{\hat{σ}}_{S M P}} = \frac{2}{3} \sqrt{\frac{({\hat{σ}}_{1} - {\hat{σ}}_{2})^{2}}{4 {\hat{σ}}_{1} {\hat{σ}}_{2}} + \frac{({\hat{σ}}_{2} - {\hat{σ}}_{3})^{2}}{4 {\hat{σ}}_{2} {\hat{σ}}_{3}} + \frac{({\hat{σ}}_{3} - {\hat{σ}}_{1})^{2}}{4 {\hat{σ}}_{3} {\hat{σ}}_{1}}} = c o n s t

where, ${\hat{σ}}_{S M P}$ and ${\hat{τ}}_{S M P}$ are normal stress and shear stress in extended SMP failure criterion, and ${\hat{σ}}_{1}$ , ${\hat{σ}}_{2}$ , and ${\hat{σ}}_{3}$ are the principal stresses for a cohesive material, and are given as

(2)

{\hat{σ}}_{1} = σ_{1} + σ_{0} {\hat{σ}}_{2} = σ_{2} + σ_{0} {\hat{σ}}_{3} = σ_{3} + σ_{0}

where, $σ_{0} = c \cot ϕ$ , and $c$ and $ϕ$ are the cohesion and friction angle of the material, respectively.

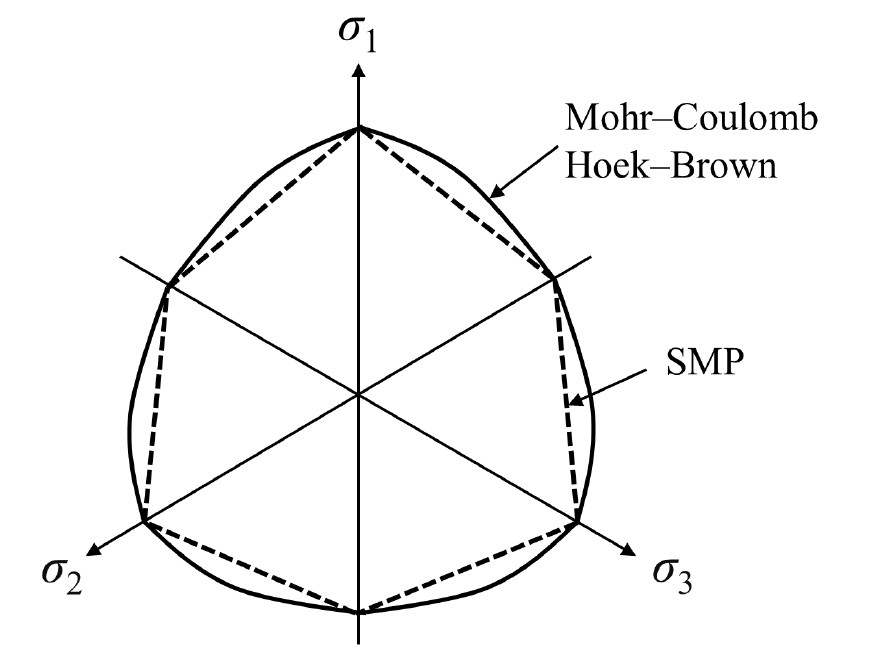
Expressing the condition on the octahedral plane yields the SMP results as a smooth curve representing the Mohr-Coulomb criterion (solid line in Fig. 3) circumscribing a hexagon (dashed lines in Fig. 3). For a cohesive material, the extended SMP failure criterion for a planar strain state can be obtained based on the following equation:

(3)

σ_{2} + σ_{0} = \sqrt{(σ_{1} + σ_{0}) (σ_{3} + σ_{0})}

The axial symmetry of the problem leads to the radial stress $σ_{r}$ and tangential stress $σ_{θ}$ in the rock mass being the principal stresses, such that $σ_{1} = σ_{r}$ and $σ_{3} = σ_{θ}$ .

For a planar strain problem, Eq. (1) is rewritten as follows:

(i) in an elastic-plastic medium

(4)

\frac{σ_{θ} + σ_{0}}{σ_{r} + σ_{0}} = \frac{1}{4} (A_{0} + \sqrt{B_{0} - 2 A_{0}} - 1)^{2} = R_{P S 0}

(ii) in an elastic-brittle medium (Fig. 2)

(5)

\frac{σ_{θ} + σ_{01}}{σ_{r} + σ_{01}} = \frac{1}{4} (A_{01} + \sqrt{B_{01} - 2 A_{01}} - 1)^{2} = R_{P S 1}

where, $A_{01} = \sqrt{8 \tan^{2} ϕ_{T C 0} + 9}$ ; $A_{1} = \sqrt{8 \tan^{2} ϕ_{T C 1} + 9}$ ; $B_{0} = \sqrt{8 \tan^{2} ϕ_{T C 0} + 6}$ ; $B_{01} = \sqrt{8 \tan^{2} ϕ_{T C 1} + 6}$ ; $σ_{0} = c_{T C 0} / \tan ϕ_{T C 0}$ ; and $σ_{01} = c_{T C 1} / \tan ϕ_{T C 1}$ . $R_{P S 0}$ and $R_{P S 1}$ represent the ratio of major stress to minor stress at the peak strength and residual strength, respectively. $ϕ_{T C 0}$ and $ϕ_{T C 1}$ are the friction angle of the initial and residual states, respectively, under triaxial compressive stress (Fig. 3).

https://static.apub.kr/journalsite/sites/kseg/2022-032-01/N0520320101/images/kseg_32_01_01_F3.jpg

Fig. 3.

Failure surfaces in the π-plane. $σ_{1}$ , $σ_{2}$ and $σ_{3}$ are the principal stresses.

Analytical Solution for Stresses and Displacement in the Plastic Region

Critical Internal Pressure $p_{0}^{c r}$

Lamé’s solutions for the elastic region are as follows (Fig. 1):

(6)

σ_{r} = p_{0} (1 - \frac{r_{i}^{2}}{r^{2}}) + p_{i} (\frac{r_{i}}{r})^{2} σ_{θ} = p_{0} (1 + \frac{r_{i}^{2}}{r^{2}}) - p_{i} (\frac{r_{i}}{r})^{2}

(7)

u = \frac{(1 + ν) (p_{0} - p_{i}) r_{i}^{2}}{E r}

An unsupported opening starts to fail when the in situ stress exceeds the critical pressure $p_{0}^{c r}$ . By assuming that the plastic zone reaches the wall of the opening, the critical internal pressure $p_{0}^{c r}$ is found by substituting Eq. (6) with $r = r_{i}$ in Eq. (4):

(8)

p_{0}^{c r} = \frac{(R_{P S 0} - 1) σ_{0}}{2}

For an opening with a supporting system (supporting force, $p_{i}$ ), when $p_{0}$ exceeds $p_{0}^{c r}$ , the minimum value of $p_{i}$ can be solved for the surroundings of the opening with no plastic zone:

(9)

p_{i}^{c r} = \frac{σ_{0} (1 - R_{P S 0}) + 2 p_{0}}{1 + R_{P S 0}}

Stresses in the Plastic Region

Substituting the equilibrium equation in Eq. (5) obtains the stress in the plastic region for the extended SMP failure criterion:

(10)

σ_{r}^{p} = - σ_{01} + (p_{i} + σ_{01}) (\frac{r_{i}}{r})^{1 - R_{P S 1}} σ_{θ}^{p} = - σ_{01} + R_{1} (p_{i} + σ_{01}) (\frac{r_{i}}{r})^{1 - R_{P S 1}}

Based on equation (10), the tangential stress $p_{y}$ on the elastic-plastic boundary is

(11)

p_{y} = σ_{r}^{p} |_{r = r_{y}} = - σ_{01} + (p_{i} + σ_{01}) (\frac{r_{i}}{r_{y}})^{1 - R_{P S 1}}

Replacing $r_{i}$ and $p_{i}$ with $r_{y}$ and $p_{y}$ in Eq. (6) yields the stress in the plastic region:

(12)

σ_{r}^{e} = p_{0} (1 - \frac{r_{y}^{2}}{r^{2}}) + p_{y} \frac{r_{y}^{2}}{r^{2}} σ_{θ}^{e} = p_{0} (1 + \frac{r_{i}^{2}}{r^{2}}) - p_{y} \frac{r_{y}^{2}}{r^{2}}

Substituting Eq. (12) with $r = r_{y}$ in Eq. (4), we obtain $p_{y}$ . Considering the radial stress continuity at the elastic-plastic boundary, the plastic radius $r_{y}$ is

(13)

r_{y} = r_{i} [\frac{σ_{0} (1 - R_{P S 0}) + σ_{01} (1 + R_{P S 0}) + 2 p_{0}}{(R_{P S 0} + 1) (p_{i} + σ_{01})}]^{\frac{1}{R_{P S 1} - 1}}

For no stress-drop or strain-softening, the radius of the plastic region can be found by replacing $σ_{0}$ and $R_{P S 0}$ with $σ_{01}$ and $R_{P S 1}$ :

(14)

r_{y 0} = r_{i} [\frac{σ_{0} (1 - R_{P S 0}) + σ_{0} (1 + R_{P S 0}) + 2 p_{0}}{(R_{P S 0} + 1) (p_{i} + σ_{0})}]^{\frac{1}{R_{P S 0} - 1}}

Displacement in the Plastic Region

According to classical plasticity theory, the total strain consists of elastic and plastic parts. For planar strain, neglecting volumetric strain, the relationship between the radial and tangential strains is

(15)

\frac{d u}{d r} + \frac{u}{r} = 0

From the condition of compatibility in the case of infinitesimal deformation, the displacement at the elastic-plastic boundary $u^{p}$ is

(16)

u^{p} = \frac{r_{y}^{2} (1 + ν) (p_{0} - p_{y})}{E r}

The displacement at the opening wall $u_{i}$ is

(17)

u_{i} = u^{p} |_{r = r_{i}} = \frac{r_{y}^{2} (1 + ν) (p_{0} - p_{y})}{E r_{i}}

The closed-form solution for the perfectly elastic-plastic problem can be obtained by replacing $σ_{01}$ and $R_{P S 1}$ with $σ_{0}$ and $R_{P S 0}$ , respectively.

Comparison of Solutions

As rocks are strain-softening materials exhibiting peak and residual strength, it is reasonable to assume that they obey elastic-brittle-plastic behavior given that the mechanical parameters are accurate. Therefore, the effects of the strength parameters and internal pressure on the convergence of the opening wall and the plastic radius in the brittle-plastic extended SMP rock mass are assessed by comparing the presented solution with the Kastner solution (based on the M-C failure criterion) in both perfect-plastic and brittle-plastic media. Table 1 lists the geometric and mechanical parameters for three cases with different residual cohesions.

Table 1.

Geometric and mechanical parameters

Extended SMP rock mass	Case 1	Case 2	Case 3
Radius of tunnel, r_i (m)	3	3	3
Initial stress, p₀ (MPa)	30	30	30
Young’s modulus, E (GPa)	15	15	15
Internal cohesion, c (MPa)	15	15	15
Residual cohesion, c_r (MPa)	2	4	6
Friction angle, 𝜙 (°)	25	25	25
Residual friction angle, 𝜙_r (°)	25	25	25

The failure stress $p_{0}^{S M P}$ and critical support pressure $p_{i}^{S M P}$ in M-C and extended SMP media can be obtained using Eqs. (8) and (9). The failure stress $p_{0}^{S M P}$ (11.8 MPa) in the extended SMP medium is larger than that in the M-C medium (9.4 MPa). The critical support pressure $p_{i}^{S M P}$ (9.5 MPa) in the extended SMP medium is smaller than that in the M-C medium (11.8 MPa). The result implies that $σ_{2}$ strengthens the opening wall in the extended SMP medium.

Perfect-Plastic Medium

Effect of Internal Cohesion and Friction Angle on the Plastic Radius

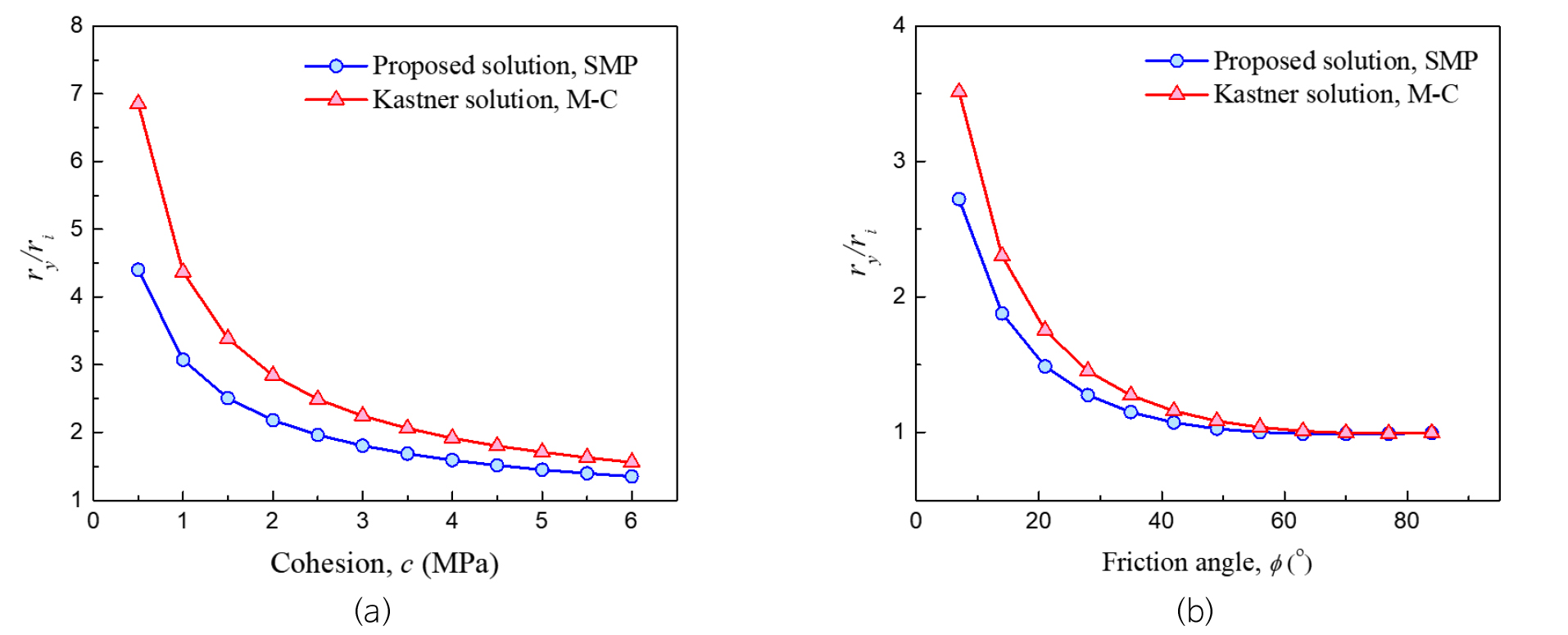
Fig. 4a shows the effect of internal cohesion on the dimensionless plastic radii in M-C and extended SMP media. The dimensionless plastic radius is the ratio of the plastic radius to the initial tunnel radius ( $r_{y} / r_{i}$ ). For c > 3 MPa, a variation in c has a slight effect on the dimensionless plastic radius. In contrast, for c < 2 MPa, any variation in c has a strong effect on $r_{y} / r_{i}$ . The ratio in the extended SMP medium is smaller than that in the M-C medium by 12.8% for c = 6 MPa and by 29.6% for c = 1 MPa.

Fig. 4b shows the effect of friction angle on the dimensionless plastic radii in the M-C and extended SMP media. The trends are similar in both media. For 20° < 𝜙 < 30°, the variation in 𝜙 has a slight effect on the ratio. In contrast, when 𝜙 < 20°, $r_{y} / r_{i}$ is strongly affected by any variation in 𝜙.

https://static.apub.kr/journalsite/sites/kseg/2022-032-01/N0520320101/images/kseg_32_01_01_F4.jpg

Fig. 4.

Effect of (a) internal friction angle and (b) cohesive force on the dimensionless plastic radii in perfect-plastic M-C and extended SMP media.

Effect of $σ_{2}$ on Displacement and Stress in the Plastic Region

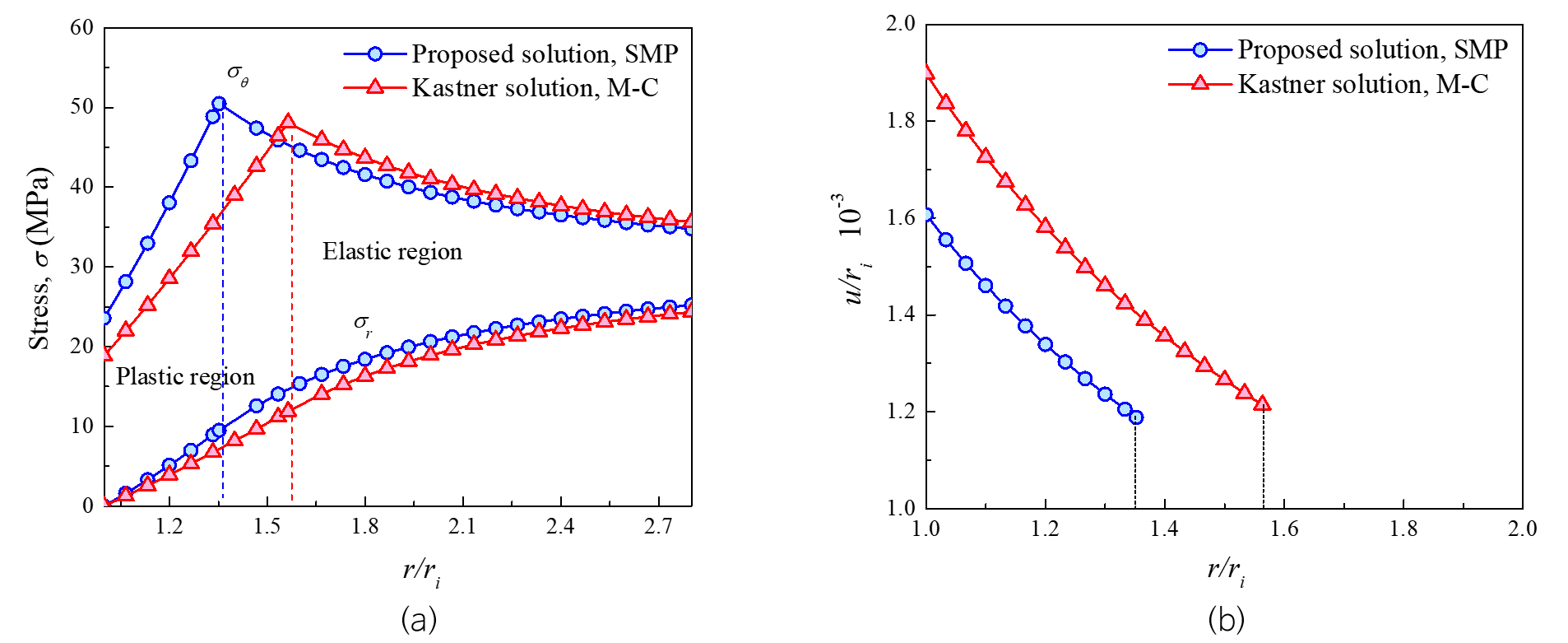
Fig. 5a shows the stresses in the M-C and extended SMP media, in the case of $p_{0}$ (30 MPa) > $p_{0}^{S M P}$ and $p_{0}^{M C}$ . The hoop stress of the opening wall $σ_{θ}^{S M P}$ in the M-C medium (23.5 MPa) is larger than that in the extended SMP medium (18.8 MPa). The maximum value of $σ_{θ}^{S M P}$ (50.5 MPa) at the elastic-plastic boundary is larger than $σ_{θ}^{M C}$ (48.2 MPa). The plastic radius $r_{y}^{S M P}$ (4.1 m) is smaller than $r_{y}^{M C}$ (4.7 m). The radial stress in the plastic region $σ_{r}^{S M P}$ is larger than $σ_{r}^{M C}$ , which implies that the rock is strengthened by $σ_{2}$ .

Fig. 5b shows the displacement in the plastic region. The plastic radius $r_{y}^{S M P}$ in the extended SMP medium is 15.6% smaller than $r_{y}^{M C}$ . The convergence displacement of the opening wall $u_{i}^{S M P}$ in the extended SMP medium is 18.7% larger than that in M-C medium $u_{i}^{M C}$ .

https://static.apub.kr/journalsite/sites/kseg/2022-032-01/N0520320101/images/kseg_32_01_01_F5.jpg

Fig. 5.

(a) Radial and hoop stresses and (b) radial displacement in perfect-plastic M-C and extended SMP media.

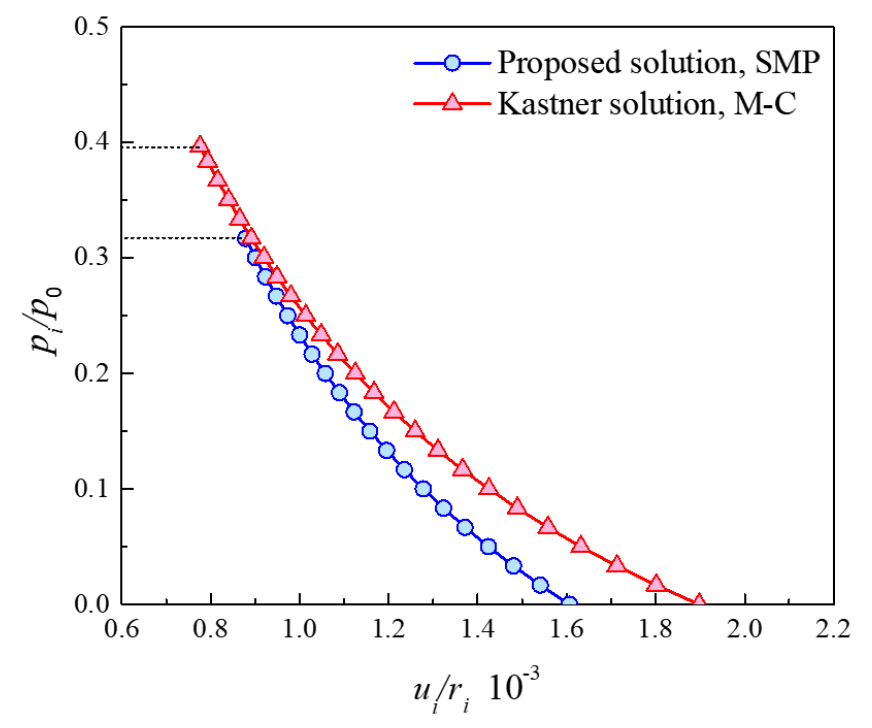
Fig. 6 shows the ground reaction curves in M-C and extended SMP perfect-plastic rock masses. The supporting force $p_{i} / p_{0}$ is decreased due to the presence of $σ_{2}$ .

https://static.apub.kr/journalsite/sites/kseg/2022-032-01/N0520320101/images/kseg_32_01_01_F6.jpg

Fig. 6.

Ground reaction curves for M-C and extended SMP perfect-plastic rock masses.

Elastic-Brittle-Plastic Medium

Effect of $σ_{2}$ on Stress, Plastic Radii, and Ground Reaction Curves

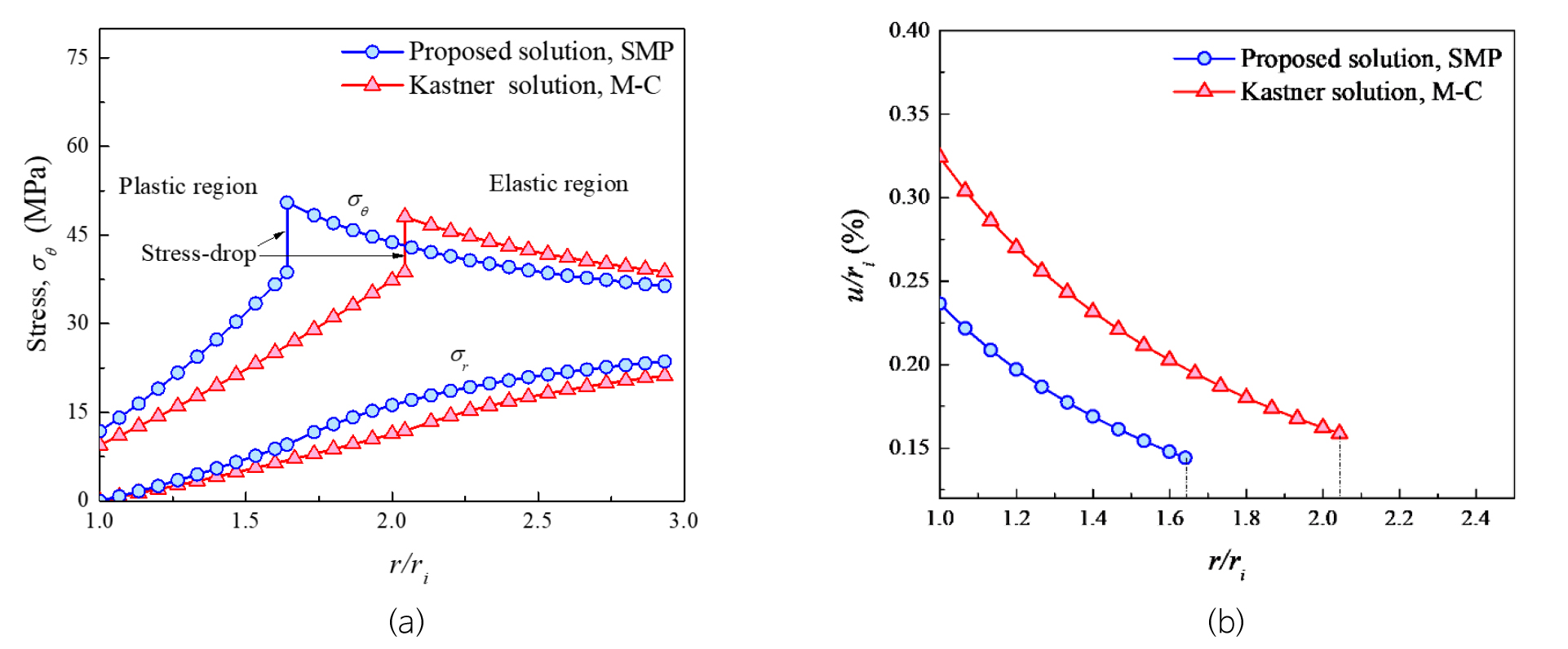
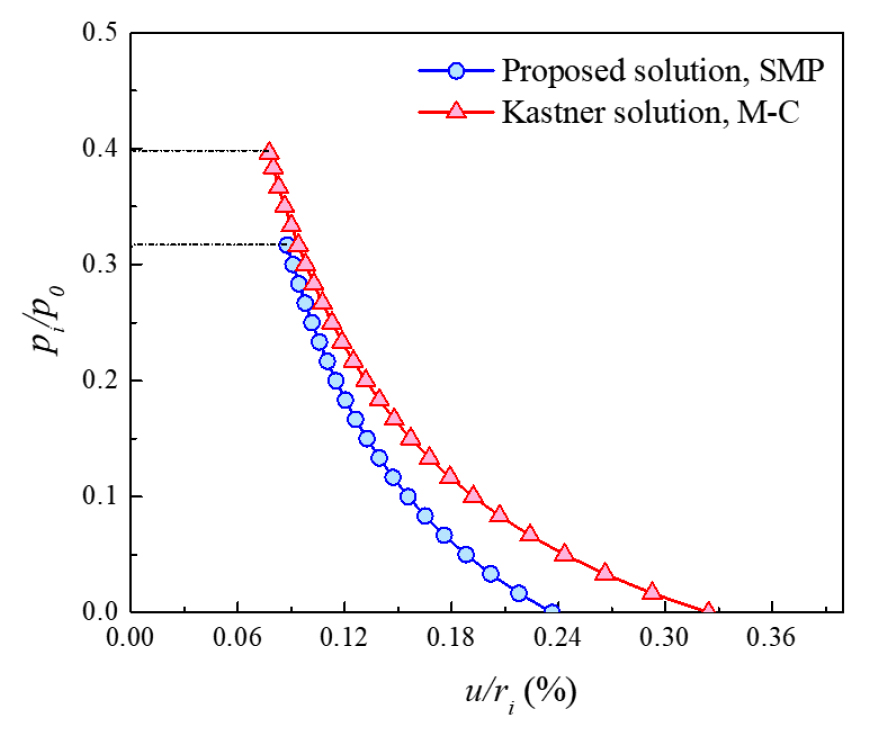
Table 1 lists the residual strength parameters for a brittle-plastic medium. Fig. 7a shows the stress and displacement in the plastic region. The plastic radius $r_{y}^{S M P}$ (4.9 m) in the extended SMP medium is smaller than $r_{y}^{M C}$ (6.1 m). The convergence displacement of the opening wall $u_{i}^{S M P}$ (4.8 mm) in the extended SMP medium is 18.7% smaller than that in the M-C medium $u_{i}^{M C}$ (5.7 mm). The radial stress in the plastic region $σ_{r}^{S M P}$ is larger than $σ_{r}^{M C}$ . The hoop stress of the opening wall $σ_{θ}^{S M P}$ in the extended SMP medium (11.7 MPa) is larger than that in the M-C medium (9.4 MPa). The maximum value of $σ_{θ}^{S M P}$ (50.5 MPa) at the elastic-plastic boundary is larger than $σ_{θ}^{M C}$ (48.2 MPa). These results suggest that the rock strength increases with increasing $σ_{2}$ . Fig. 7b shows that the plastic radius $r_{y}^{S M P}$ (4.9 m) is 24.6% smaller than $r_{y}^{M C}$ (6.13 m) and that $u_{i}^{S M P}$ (7.1 mm) in the extended SMP medium is 37.3% smaller than that in the M-C medium $u_{i}^{M C}$ (9.7 mm). Fig. 8 shows that the supporting force ( $p_{i} / p_{0}$ ) in the extended SMP medium is smaller than that in the M-C medium, and the dimensionless convergence displacement ( $u / r_{i}$ ) in the extended SMP medium is also smaller than that in the M-C medium. These results indicate that the rock strength is significantly affected by $σ_{2}$ .

https://static.apub.kr/journalsite/sites/kseg/2022-032-01/N0520320101/images/kseg_32_01_01_F7.jpg

Fig. 7.

(a) Radial and hoop stresses and (b) dimensionless radial displacement in M-C and extended SMP brittle-plastic media.

https://static.apub.kr/journalsite/sites/kseg/2022-032-01/N0520320101/images/kseg_32_01_01_F8.jpg

Fig. 8.

Ground reaction curves for M-C and extended SMP brittle-plastic rock masses.

Effect of Strength Reduction on Plastic Radius and Opening Wall Convergence

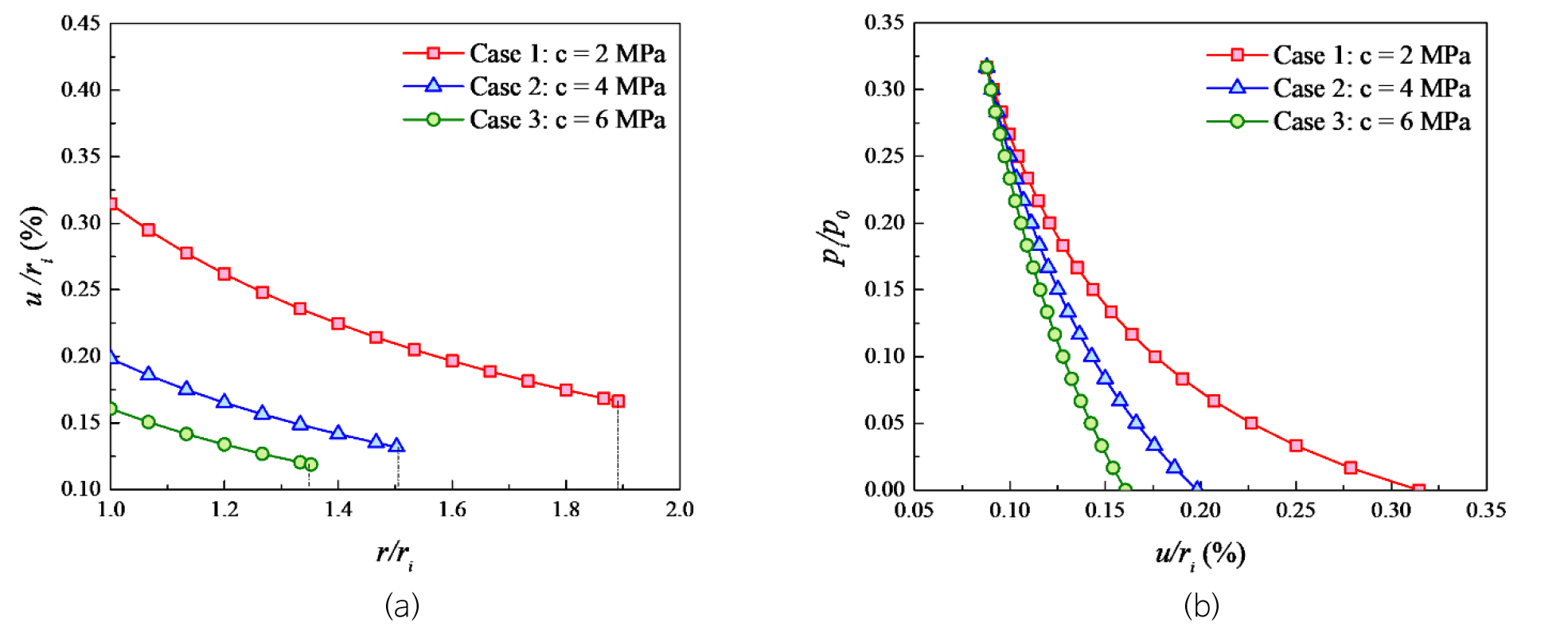
Fig. 9a shows the effects of residual cohesion on the dimensionless radial displacement of the opening ( $u / r_{i}$ ). The plastic radius $r_{y}^{S M P}$ increases by 24% as the residual cohesion decreases from 6 to 2 MPa. In addition, the critical supporting force ( $p_{i} / p_{0}$ ) was not affected by the reduction in residual cohesion (Fig. 9b). The displacement of the plastic region increases by 100% as the residual cohesion is reduced from 6 to 2 MPa.

https://static.apub.kr/journalsite/sites/kseg/2022-032-01/N0520320101/images/kseg_32_01_01_F9.jpg

Fig. 9.

(a) Dimensionless radial displacement and (b) ground reaction curves for an extended SMP brittle-plastic rock mass.

Conclusions

To estimate the effects of the intermediate principal stress on the plastic zone and the convergence of circular excavation in an elastic-brittle-plastic medium, closed-form solutions for both M-C and extended SMP media are presented for stresses and displacements in the plastic region.

The results for displacements and stresses are compared with the Kastner solution. The plastic radius and displacement obtained for an extended SMP medium increase significantly compared with those obtained for an M-C medium. The solutions can be used to investigate the effects of internal pressure on the convergence of opening and the extent of the plastic region in a brittle-plastic medium. The strength in the residual plastic region is higher in the extended SMP medium than in the M-C medium. For a decreasing residual strength of the rock mass, the opening wall convergence increases sharply when the residual cohesion decreases substantially from 6 to 2 MPa. This means that the stability of the underground opening is enhanced by the intermediate principal stress and the critical supporting pressure is decreased, which reduces the cost of the supporting system.

Acknowledgements

This work was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (No. 2019R1A6A1A03033167).

References

Alonso, E., Alejano, L.R., Varas, F., Fdez-Manin, G., Carranza-Torres, C., 2003, Ground response curves for rock masses exhibiting strain-softening behaviour, International Journal for Numerical and Analytical Methods in Geomechanics, 27(13), 1153-1185. 10.1002/nag.315

Brown, E.T., Bray, J.W., Ladanyi, B., Hoek, E., 1983, Ground response curves for rock tunnels, Journal of Geotechnical Engineering, 109(1), 15-39. 10.1061/(ASCE)0733-9410(1983)109:1(15)

Carranza-Torres, C., Fairhurst, C., 1999, The elasto-plastic response of underground excavations in rock masses that satisfy the Hoek-Brown failure criterion, International Journal of Rock Mechanics and Mining Sciences, 36(6), 777-809. 10.1016/S0148-9062(99)00047-9

Detournay, E., 1986, Elastoplastic model of a deep tunnel for a rock with variable dilatancy, Rock Mechanics and Rock Engineering, 19(2), 99-108. 10.1007/BF01042527

Egger, P., 2000, Design and construction aspects of deep tunnels (with particular emphasis on strain softening rocks), Tunnelling and Underground Space Technology, 15(4), 403-408. 10.1016/S0886-7798(01)00008-6

Fahimifar, A., Ghadami, H., Ahmadvand, M., 2015, An elasto-plastic model for underwater tunnels considering seepage body forces and strain-softening behaviour, European Journal of Environmental and Civil Engineering, 19(2), 129-151. 10.1080/19648189.2014.939305

Katebian, E., Molladavoodi, H., 2017, Practical ground response curve considering post-peak rock mass behaviour, European Journal of Environmental and Civil Engineering, 21(1), 1-23. 10.1080/19648189.2015.1090928

Matsuoka, H., Sun, D.A., 1995, Extension of spatially mobilized plane (SMP) to frictional and cohesive materials and its application to cemented sands, Soils and Foundations, 35(4), 63-72. 10.3208/sandf.35.4_63

Nakai, T., Matsuoka, H., 1983, Shear behaviors of sand and clay under three-dimensional stress conditions, Soil and Foundatiuons, 23(2), 26-42. 10.3208/sandf1972.23.2_26

Ogawa, T., Lo, K.Y., 1987, Effects of dilatancy and yield criteria on displacements around tunnels, Canadian Geotechnical Journal, 24(1), 100-113. 10.1139/t87-009

Osman, A.S., Randolph, M.F., 2011, Analytical solution for the consolidation around a laterally loaded pile, International Journal of Geomechanics, 12(3), 199-208. 10.1061/(ASCE)GM.1943-5622.0000123

Park, K.H., Kim, Y.J., 2006, Analytical solution for a circular opening in an elastic-brittle-plastic rock, International Journal of Rock Mechanics and Mining Sciences, 43(4), 616-622. 10.1016/j.ijrmms.2005.11.004

Sharan, S.K., 2003, Elastic-brittle-plastic analysis of circular openings in Hoek-Brown media, International Journal of Rock Mechanics and Mining Sciences, 40(6), 817-824. 10.1016/S1365-1609(03)00040-6

Sharan, S.K., 2005, Exact and approximate solutions for displacements around circular openings in elastic-brittle-plastic Hoek-Brown rock, International Journal of Rock Mechanics and Mining Sciences, 42(4), 542-549. 10.1016/j.ijrmms.2005.03.019

Wang, S., Yin, X., Tang, H., Ge, X., 2010, A new approach for analyzing circular tunnel in strain-softening rock masses, International Journal of Rock Mechanics and Mining Sciences, 47(1), 170-178. 10.1016/j.ijrmms.2009.02.011

Wang, Y., 1996, Ground response of circular tunnel in poorly consolidated rock, Journal of Geotechnical Engineering, 122(9), 703-708. 10.1061/(ASCE)0733-9410(1996)122:9(703)

Zareifard, M.R., Fahimifar, A., 2014, Effect of seepage forces on circular openings excavated in Hoek-Brown rock mass based on a generalized effective stress principle, European Journal of Environmental and Civil Engineering, 18(5), 584-600. 10.1080/19648189.2014.891470

Zhao, H., Shi, C., Zhao, M., Li, X., 2016, Statistical damage constitutive model for rocks considering residual strength, International Journal of Geomechanics, 17(1), 04016033. 10.1061/(ASCE)GM.1943-5622.0000680

The Journal of Engineering Geology ISSN:1226-5268(Print) 2287-7169(Online) 지질공학

Preview

A Closed-Form Solution for Circular Openings in an Elastic–Brittle–Plastic Extended Spatial Mobilized Plane Medium

ABSTRACT

MAIN

Fig. 1.

A circular opening in an infinite medium. ri and ry are the radii of the tunnel and plastic region, respectively. p is the internal pressure and p0 is the hydrostatic stress of the rock mass.

Fig. 2.

Relationship between stress and strain for an elastic-brittle-plastic medium.

(1)

(2)

(3)

(4)

(5)

Fig. 3.

Failure surfaces in the π-plane. σ1, σ2 and σ3 are the principal stresses.

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

Table 1.

Geometric and mechanical parameters

Fig. 4.

Effect of (a) internal friction angle and (b) cohesive force on the dimensionless plastic radii in perfect-plastic M-C and extended SMP media.

Fig. 5.

(a) Radial and hoop stresses and (b) radial displacement in perfect-plastic M-C and extended SMP media.

Fig. 6.

Ground reaction curves for M-C and extended SMP perfect-plastic rock masses.

Fig. 7.

(a) Radial and hoop stresses and (b) dimensionless radial displacement in M-C and extended SMP brittle-plastic media.

Fig. 8.

Ground reaction curves for M-C and extended SMP brittle-plastic rock masses.

Fig. 9.

(a) Dimensionless radial displacement and (b) ground reaction curves for an extended SMP brittle-plastic rock mass.

Acknowledgements

References

A circular opening in an infinite medium. $r_{i}$ and $r_{y}$ are the radii of the tunnel and plastic region, respectively. $p$ is the internal pressure and $p_{0}$ is the hydrostatic stress of the rock mass.

Failure surfaces in the π-plane. $σ_{1}$ , $σ_{2}$ and $σ_{3}$ are the principal stresses.