서 론
연구지역의 DFN 및 실내 역학시험
연구지역의 지질 및 절리의 기하학적 특성
신선암 및 절리의 역학적 특성
절리성 암반의 강도 및 변형
해석절차
3DEC 입력변수
DFN 블록의 강도 및 변형 특성 추정
결과 및 토의
결 론
서 론
자연상에서 암반(rock masses)은 신선암(intact rock)과 절리, 단층, 층리, 전단대, 암맥 등 불연속면의 조합으로 형성된 경우가 대부분이다. 절리성 암반의 강도와 변형은 암종과 관련된 신선암의 역학적 특성과 불연속절리망(discrete fracture network, DFN)의 기하학적 특성 및 불연속면의 역학적 특성에 크게 영향을 받는다. 또한, 절리성 암반의 강도 및 변형을 좌우하는 요인으로 현지응력(in-situ stress) 조건, 지하수 상태, 응력의 재하/제하 경로 등을 들 수 있다. 암반의 강도와 변형에 대한 확고한 이해는 지질공학 관련 인프라에 대한 설계 및 안정성 평가에 있어서 필수적이다. 현장의 절리성 암반은 대부분 기하학적으로 복잡한 패턴의 절리를 수반한다. 절리의 기하학적 특성에 내재한 변동성과 현지응력 평가의 불확실성은 절리성 암반에 대한 강도 및 변형 추정을 어렵게 하는 요인으로 작용한다. 이는 절리성 암반의 역학적 특성이 절리분포로 인하여 규모 의존성 및 이방성을 나타내는 경우가 대부분이기 때문이다.
절리성 암반의 강도 및 변형 특성을 추정하는 방법은 직접적 및 간접적 방법으로 분류할 수 있다. 직접적인 방법은 실내 및 현장시험을 통하여 이루어진다. 실내 실험실 규모의 시료는 일반적으로 크기의 제약이 따르며 시험 결과는 시료의 크기에 따라 유의미한 차이를 도출한다. 그동안 절리성 암반의 강도 및 변형에 미치는 시험 규모의 영향을 파악하기 위해 많은 현장시험이 수행되었다. 초창기 Bieniawski(1978)와 Heuze(1980)는 암반의 강도와 변형에 대한 규모효과(scale effect)를 규명하기 위하여 다양한 현장시험 결과를 고찰하고 절리성 암반에 대한 시험 규모의 증가에 따른 강도의 저하와 변형의 증대를 보고하였다. 또한, Bieniawski(1978)는 현장시험 결과를 바탕으로 절리의 분포 및 상태를 고려한 암반의 변형계수 추정법을 제안하였는데, 연구지역에 한정된 국지적인 암반모델이 적용되었으며 이에 따른 결과를 일반화하기에는 어려움이 있다(Ryu et al., 2020). 이는 절리성 암반의 역학적 특성에 대한 현실적인 추정을 위하여 다양한 패턴의 절리 조합이 설정된 광범위한 수량의 시험이 유의미한 응력 수준 및 응력 경로 하에서 수행되어야 하나 이러한 현장시험 프로그램을 고안하고 실행하는 것은 거의 불가능하기 때문이다.
절리성 암반의 강도 및 변형 특성을 간접적으로 추정하기 위하여 지질공학 현장에서 가장 많이 사용되는 기법은 암반 분류지수와 암반의 역학적 특성 간의 경험적 상관성을 활용하는 방법인데, 암반 분류지수는 스칼라양(scalar)이므로 암반의 이방성 및 규모 종속적 특성을 고려할 수 없는 단점이 있다. 따라서 간접적인 강도정수 추정법은 수치해석 기법을 활용하는 추세로 발전하고 있으며, 이는 현장의 절리성 암반을 대표하는 DFN을 구성하고 신선암과 절리의 강도 및 변형 특성을 바탕으로 신선암과 절리의 상호작용을 고려하여 수치해석을 수행하는 방식이다. 절리성 암반의 강도 및 변형 특성 추정을 위한 수치해석 방법은 유한요소법(finite element method) 또는 개별요소법(distinct element method)이 주를 이룬다(Kulatilake, 1985; Cundall, 1988; Hart et al., 1988).
개별요소법은 해석영역을 가로지르는 무한 길이의 절리에 의해 형성된 블록상 암반에 대한 응력-변형 해석 수행에 유용하다(Cundall, 1971, 1988; Lemos et al., 1985; Hart et al., 1988; Ryu and Um, 2021). 개별요소법에서 암반은 강체 또는 변형 가능한 다면체 블록의 집합체로 모사되며 절리는 블록 간 상호작용의 경계로 취급된다. 개별요소 알고리듬은 블록 개체에 대한 연속체 이론과 더불어 블록 간에 작용하는 힘-변위 법칙과 블록에 작용하는 불균형적 힘에 의한 개별 블록의 움직임을 고려하는 운동 법칙을 포함한다. 이처럼 신선암 블록과 절리의 상호작용을 고려하는 개별요소법은 다양한 응력 및 변위의 경계조건에서 암반 블록 시스템의 역학적 거동을 효과적으로 해석할 수 있다.
개별요소법을 적용하기 위한 해석영역은 이차원 해석에서 다각형 또는 삼차원 해석에서 다면체로 이산화(discretization)되어야 한다. 그러나 유한 길이의 절리 분포로 이루어진 해석영역은 절리 경계만으로 이산화할 수 없다. 저자는 선행연구를 통하여 삼차원 해석영역에 가상절리를 체계적으로 추가하여 해석영역을 실제절리와 가상절리로 규정된 다면체 블록으로 이산화하는 방법론을 논의하였으며 해석영역에 추가된 가상절리의 역학적 거동이 신선암의 거동과 유사하도록 설정하기 위한 가상절리의 물성에 대하여 보고하였다(Ryu et al., 2020). 가상절리를 도입한 개별체 해석은 유한 길이의 절리를 고려하여 응력-변형 해석을 수행할 수 있는 장점이 있지만, 절리의 체적빈도 증가 또는 해석영역의 증대에 따른 다면체 블록요소 개수의 기하급수적 증가로 인하여 현장적용 시 연산 시간과 관련된 실무적 어려움도 있다. 본 연구는 부산 기장지역의 백악기 흑운모 화강암이 분포하는 절리성 암반에 대하여 삼차원 개별요소법 기반의 수치해석을 수행하고 해석영역의 크기가 절리성 암반의 강도 및 변형 특성에 미치는 영향을 평가하였다. 또한, 사례현장에 대한 삼차원 구성모델(constitutive model)을 도출하였으며 현장 규모(field scale)의 응력-변형 해석을 위한 작업흐름(workflow)를 제시하였다.
연구지역의 DFN 및 실내 역학시험
연구지역의 지질 및 절리의 기하학적 특성
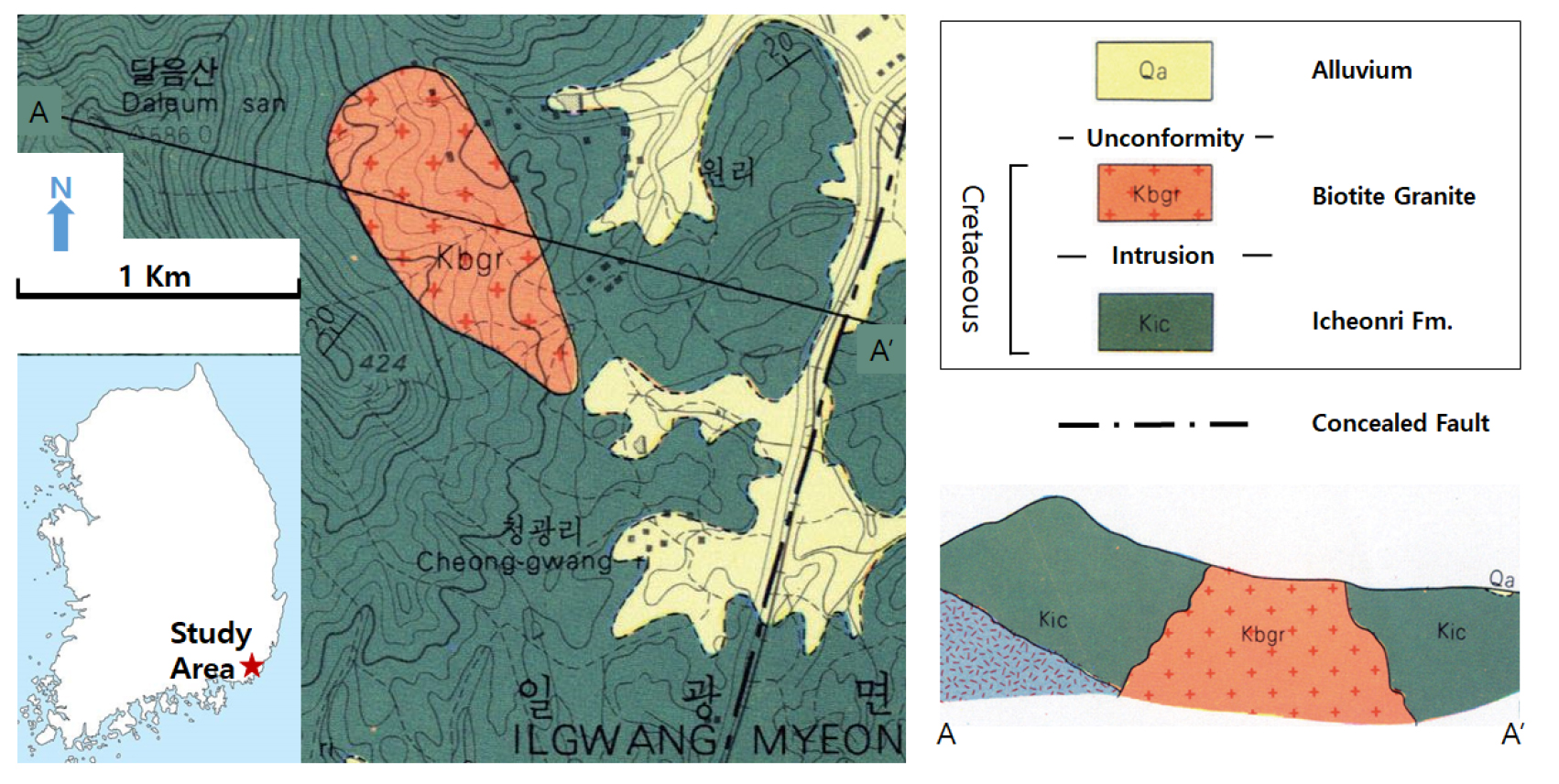
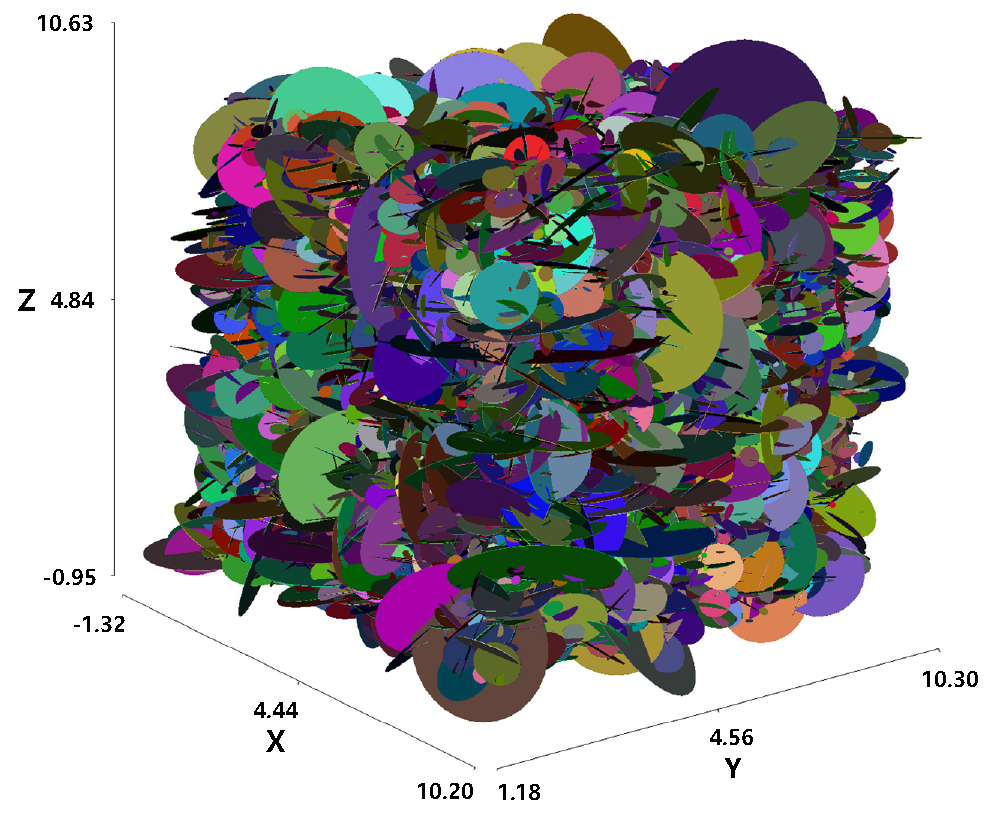
연구지역은 부산광역시 기장군 일광면 원리 일대이며 이천리층을 관입한 백악기 흑운모 화강암으로 이루어진 절리성 암반이 분포한다. Fig. 1은 흑운모 화강암이 분포하는 연구지역 및 주변의 지질도이며 화강암의 주 구성 광물은 석영, 장석 및 흑운모이다. 현장에 대한 조사선 조사(scanline survey) 및 시추공 검층을 통하여 세 개의 절리군이 구분되었다. 구분된 각각의 절리군에 대한 방향성, 간격 및 연장성을 분석한 결과가 Table 1에 요약되어 있으며 이를 바탕으로 몬테칼로 모사 기법(Monte-Carlo simulation)을 이용하여 연구지역의 절리성 암반에 대한 삼차원 DFN이 추계론적으로 구현되었다. Fig. 2는 연구지역 절리성 암반에 대하여 생성된 절리의 중심 좌표가 9 m 큐브 영역 내에 위치하는 DFN을 구현한 결과이며, 여기서 X축은 동쪽, Y축은 북쪽, Z축은 고도이다. 이와 같은 DFN 구현을 위한 절차 및 방법론은 선행연구(Choi et al., 2010; Noh and Um, 2012)를 참고할 수 있다.
Table 1.
Input parameters to generate the DFN for the study area
신선암 및 절리의 역학적 특성
절리성 암반의 응력-변형 특성은 절리성 암반을 구성하는 신선암 및 절리의 역학적 특성에 지대한 영향을 받는다. 본 연구는 연구지역에 분포하는 흑운모 화강암의 코어시료에 대하여 신선암 및 자연절리의 역학적 특성을 파악하기 위한 실내 암석역학시험을 수행하였다. 암석역학시험에 사용된 시료는 현장시추로부터 얻어진 NX 크기의 코어시료이며 신선암의 밀도, 일축압축강도(qu), 영률(E), 포아송비(ν) 측정을 위하여 각각 4회의 시험이 수행되었다(Fig. 3a & 3b). 또한, 6회의 간접인장시험과 점착력(C)과 내부마찰각(Φ)을 추정하기 위한 삼축압축시험이 수행되었다(Fig. 3c). 절리의 전단강성(joint shear stiffness, JKS), 절리점착력(Cj), 절리마찰각(Φj) 등의 절리 물성은 직접전단시험을 수행하여 추정하였으며 절리의 수직강성(joint normal stiffness, JKN)은 절리면압축시험을 통하여 결정하였다. Table 2는 연구지역의 신선암 및 절리에 대한 암석역학시험 결과를 수록하였다.
Table 2.
Mechanical properties obtained for biotite granite from the study area
총 4개의 시료로부터 측정한 신섬암의 밀도는 2,633~2,741 kg/m3 범위로 평균 2,702 kg/m3, 표준편차 47 kg/m3이다. 신선암의 일축압축시험은 0.5 MPa/s의 가압속도로 재하하였으며, 평균 일축압축강도 및 E는 각각 223.9 MPa, 57.3 GPa로 측정되었는데, 이는 ISRM 기준으로 매우 강함에 해당한다. 여기서, E는 일축압축강도의 45~55% 구간에서 접선계수(tangent modulus)로 추정된 값이다. 평균 ν는 0.29로 산정되었다. 간접인장시험은 약 200 N/s의 가압속도로 총 6회 실시되었으며, 평균 인장강도는 19.0 MPa로 평가되었다. 삼축압축시험은 Fig. 3c의 훅셀(Hoek cell)에 의하여 수행되었으며 점착력과 내부마찰각은 각각 38.8 MPa, 57.3°로 결정되었다.
절리면에 대한 일축압축시험을 통하여 측정한 JKN은 83.7 GPa/m이며 직접전단시험을 통한 JKS, 절리점착력, 절리마찰각은 각각 5.9 GPa/m, 0.22 MPa, 36.3°로 평가되었다. 이와 같은 신선암 및 절리의 역학적 특성은 연구지역의 절리성 암반에 대한 삼차원 응력-변형 해석의 입력변수로 활용되었다. 본 연구의 삼차원 응력-변형 수치해석은 개별요소법 기반의 상용코드인 3DEC(Itasca, 2016)을 이용하였다.
절리성 암반의 강도 및 변형
해석절차
3DEC 코드를 이용한 절리성 암반의 응력-변형 해석을 위해서 전체 해석영역은 절리 경계의 다면체로 이산화되어야 한다(Cundall, 1988). 일반적으로 본 연구와 같이 유한 길이의 절리로 이루어진 해석영역은 절리만으로 이산화할 수 없다. Ryu et al.(2020)은 개별요소법을 통한 절리성 암반의 삼차원 응력-변형 해석을 위하여 해석영역에 분포하는 유한 길이의 절리에 가상절리(fictitious joints)를 추가 ‧ 결합하여 해석영역을 다면체 요소로 이산화하는 절차를 제시한 바 있는데, 가상절리의 실제 역학적 거동은 알고리즘 처리 단계에서 신선암의 거동과 유사하도록 설정하는 것이 중요하다.
연구지역의 절리성 암반에 대한 삼차원 DFN 모델은 15 m × 15 m × 15 m 체적에서 10만 개 이상의 절리를 포함한다. 해석영역에 가상절리를 추가하여 개별요소로 이산화하는 방법은 해석영역이 절리를 많이 포함하지 않았을 때 매우 유용하게 활용될 수 있지만, 해석영역의 규모가 증가하거나 삼차원 절리빈도가 높아질수록 추가되는 가상절리의 수도 증가하며 이에 따른 다면체 요소 개수의 증대는 수치해석을 위한 연산 시간을 증가시킨다. 추계론적 DFN은 절리 디스크 크기의 확률분포로 음지수분포 또는 감마분포의 채택이 보편적인데(Priest, 1993), 이에 따라 매우 작은 크기의 절리가 다량 생성되는 경우가 대부분이다. 연구지역의 DFN은 디스크의 크기가 0.5 m 이하인 절리를 모두 제거하더라도 약 9만4천 개의 절리를 포함하며, 이는 현재의 컴퓨터 성능으로도 연산 수행을 매우 어렵게 하는 요인이다.
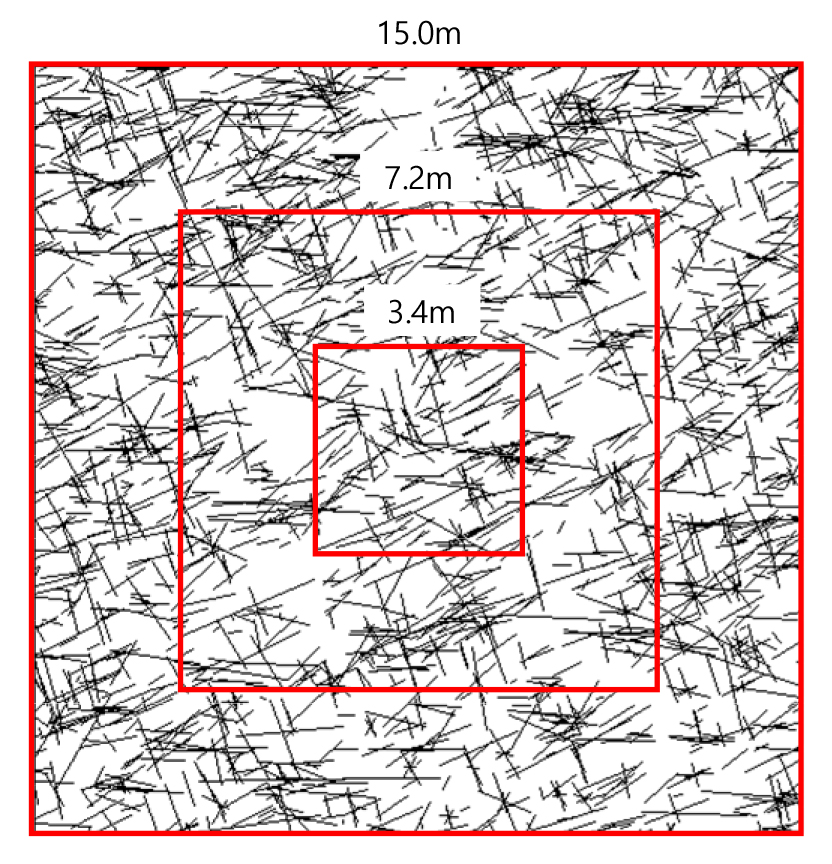
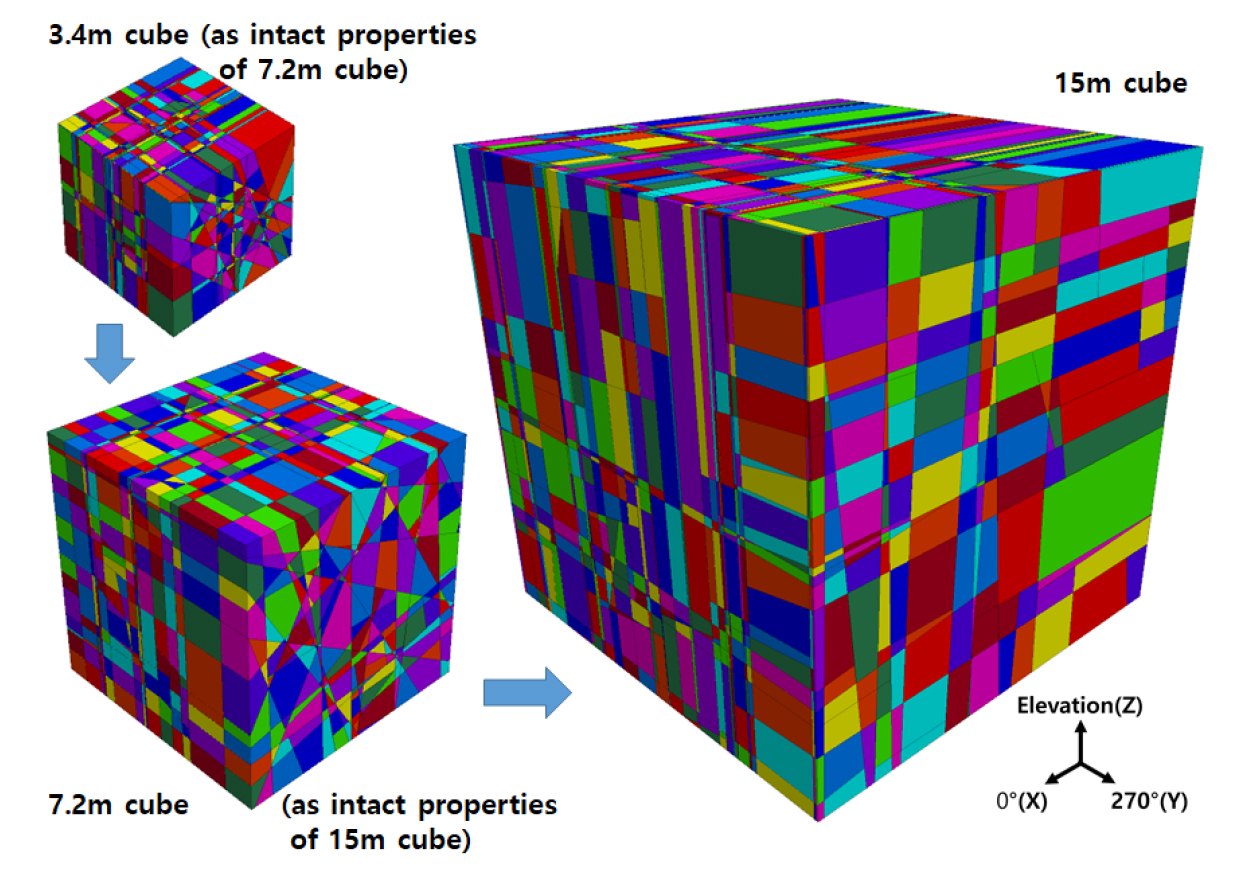
Kulatilake et al.(2004)은 스웨덴의 고준위 방사성폐기물 처분부지에 위치한 Ӓspӧ HRL의 지하 485 m 지점에서 한 변이 30 m인 정육면체 큐브 영역의 절리성 암반에 대한 응력-변형 해석을 위하여 초기 해석영역을 9.5 m 큐브로 설정하고 최종 해석영역(30 m 큐브)까지 단계별로 점진적으로 큐브 크기를 늘려가며 연산을 수행하는 방식으로 개별체-등가연속체 혼합 해석절차를 제안하였다. 여기서, 단계별 큐브의 크기를 선정하는 방법은 첫 번째 30 m 큐브에 생성된 절리 디스크의 직경을 기준으로 상위 16개 절리를 선별한 후 이들 중 가장 작은 절리의 직경(D16)을 기록한다. 두 번째 큐브는 중점을 첫 번째 30 m 큐브의 중점에 일치시키고 한 변의 크기가 D16인 큐브를 설정하였다. 이러한 절차는 큐브에 생성된 절리 디스크가 16개 이하가 될 때까지 반복되었으며 이에 따른 단계별 큐브 크기가 잠정적으로 결정되었다. 이때 가장 큰 해석영역인 30 m 큐브를 제외한 단계별 큐브는 큐브의 크기와 거의 비슷한 사이즈의 절리디스크를 포함하며 유의미한 개수의 절리가 큐브의 외각 경계면에 의해 끊길 수 있는데, 이들 절리는 30 m 큐브의 전체 해석영역에서는 해석경계에 의한 절삭이 발생하지 않을 가능성이 크다. 따라서 30 m 큐브를 제외한 모든 단계별 큐브는 절리가 해석영역 경계에 의해 끊기는 상황을 고려하기 위하여 해석영역 한 변의 크기를 앞에서 잠정적으로 결정한 절리의 최대 지름에 큐브 내에 포함하는 절리 디스크의 평균 지름을 더한 값으로 설정하였다. Kulatilake et al.(2004)은 Ӓspӧ HRL의 DFN 시스템에 대한 단계별 큐브가 16개 이하의 절리를 포함하도록 설정하였는데, 이는 당시의 PC 성능을 고려하였기 때문이다. 본 연구는 연구지역에 발달한 비교적 짧은 절리 길이분포를 고려하여 15 m 큐브를 최종 해석영역으로 결정하였으며 유사한 방식으로 30개 이하의 절리 개수를 포함하는 총 세 단계(15 m, 7.2 m, 3.4 m)의 큐브 크기를 선정하였다(Fig. 4). Fig. 5는 3.4 m, 7.2 m, 15 m 큐브 영역에서 각각의 DFN 시스템에 가상절리를 추가하여 다면체의 개별요소로 구성한 단계별 해석영역을 보여준다.
단계별 큐브의 크기는 큰 큐브에서 큐브의 크기를 줄여가며 결정하였지만, 큐브 블록에 대한 응력-변형 해석은 가장 작은 큐브로부터 출발하여 큰 큐브로 전이하며 수행하는 방식이다. 본 연구는 가장 작은 크기인 3.4 m 큐브에 대하여 가상절리를 추가하여 다면체 개별요소로 이산화하고 3DEC 기반의 응력-변형 해석을 수행하여 큐브 블록에 대한 등가의 연속체 특성을 추정하였다. 3.4 m 큐브에 포함된 절리와 신선암이 결합된 효과를 반영하는 등가의 연속체 물성은 중간단계 크기인 7.2 m 큐브에서 신선암의 물성으로 사용되었으며, 7.2 m 큐브에 분포하는 30개 절리에 가상절리를 추가하여 7.2 m 큐브 영역에 대한 등가의 연속체 물성이 추정되었다. 마지막으로 15 m 큐브에 대해서도 DFN에 가상절리를 추가하였으며 전단계인 7.2 m 큐브에 대한 등가의 연속체 물성을 신선암의 물성으로 취급하여 응력-변형 해석이 수행되었다.
3DEC 입력변수
3DEC을 활용한 삼차원 응력-변형 해석에 있어서 해석영역에 추가한 가상절리의 거동은 신선암과 유사하도록 설정되어야하며 Kulatilake et al.(1992)은 신선암의 전단탄성계수(G)와 가상절리의 JKS 비(G/JKS)가 0.008~0.012 m 범위, 그리고 가상절리의 JKN은 JKS의 2~3배 범위가 적당하다고 보고하였다. 본 연구는 큐브 해석영역에서 다면체 요소의 모든 경계를 가상절리로 가정하였을 때 큐브의 거동특성이 신선암의 역학적 거동특성과 일치하도록 최적의 JKN, JKS 값을 도출하였다. 본 연구의 수치해석에서 신선암의 역학적 거동은 tension cut-off를 포함하는 Mohr-Coulomb 파괴기준의 선형탄성-완전소성 모델을 채택하였다. 절리의 전단응력-전단변위 관계는 최대 전단강도까지는 선형탄성 모델을 적용하였고 이후부터는 완전소성 모델을 적용하였다. 본 연구의 신선암 및 자연절리의 역학적 특성은 Table 2에 요약하였으며 가상절리의 역학적 물성은 Table 3에 요약하였다.
Table 3.
Mechanical properties used to represent fictitious joints in cubic blocks of different sizes
DFN 블록의 강도 및 변형 특성 추정
DFN 시스템에서 서로 다른 절리군의 존재는 역학적 이방성을 초래할 수 있다. 본 연구는 DFN 큐브 블록에 대하여 직교하는 세 방향으로 지향적(directional) 강도 및 변형 파라미터를 추정하는 방식으로 응력-변형 해석을 수행하였다. 수치해석 결과는 DFN 큐브 블록의 직교이방성 구성모델(orthotropic constitutive model)을 수립하는데 활용할 수 있으며 구성모델로 설명되는 등가의 연속체 특성은 다음 단계의 더욱 큰 DFN 큐브 블록에서 신선암의 연속체 물성으로 사용할 수 있다. 이와 같은 응력-변형 해석절차는 개별체 해석소프트웨어에 직교이방성 구성모델을 적용하는 기능이 포함된 경우에 가능하지만, 현재 신선암에 대하여 직교이방성 구성모델을 고려하는 개별체 해석 모듈은 상용화되지 못한 실정이다. 따라서 본 연구는 작은 크기의 해석영역 단계에서 큰 크기의 해석영역 단계로 전이할 때 암반의 이방성을 고려하기 위하여 다음과 같은 절차를 채택하였다.
암반의 강도 및 변형 파라미터는 직교하는 x, y, z 세 방향에 대하여 개별적으로 추정되었다. 예로서 가장 작은 DFN 큐브 블록에서 y 방향으로 산정된 강도 및 변형 파라미터는 신선암과 절리의 영향을 결합한 y 방향으로의 등가연속체 물성으로 취급하여 다음 단계 큐브 블록의 y 방향 해석에 사용되었다. 이러한 방법은 특정 블록 크기에서 다음 단계의 더 큰 블록 크기를 거쳐 가장 큰 블록의 해석영역에 이르기까지 반복되었다. 또한, 같은 방식으로 x 및 z 방향에 대해서도 단계별 수치해석이 수행되었으며 직교하는 세 방향으로 암반의 강도 및 변형에 대한 규모효과(scale effect)가 평가되었다.
3DEC을 활용하여 DFN 큐브 블록의 블록강도, 변형계수, 포아송비 등의 강도 및 변형 파라미터를 추정하기 위한 응력 경로(stress path)는 Fig. 6에서와 같이 큐브 블록에 대하여 직교하는 x, y, z 방향으로 1 MPa의 구속압을 재하한 후 두 방향의 큐브 경계면에서 정압을 유지하고 세 번째 방향으로 블록이 완전소성변형에 이르기까지 0.05 m/s의 속도로 재하 하도록 설정하였다. 이와 같은 응력 경로는 직교하는 세 방향에 대하여 개별적으로 반복되었다. 각각의 블록에서 응력 변화에 따른 변위는 큐브 블록의 경계면에 격자형으로 설정된 총 9개의 모니터링 포인트를 통하여 기록되었으며 이들의 평균값을 사용하여 블록의 응력-변형 특성이 평가되었다. 응력-변형 다이어그램은 DFN 시스템의 블록강도와 변형계수 추정에 사용되었다.
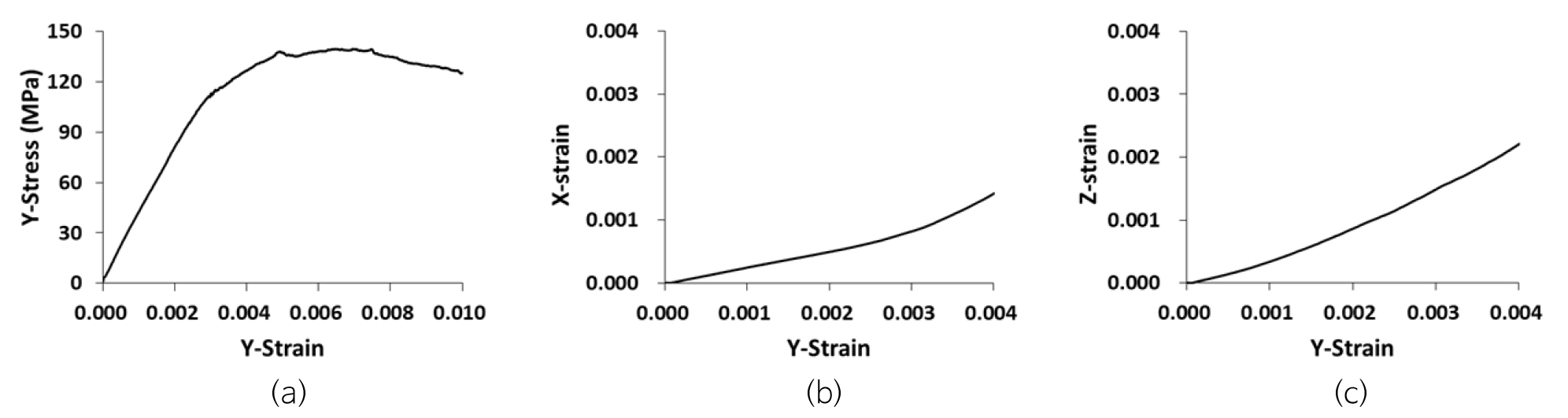
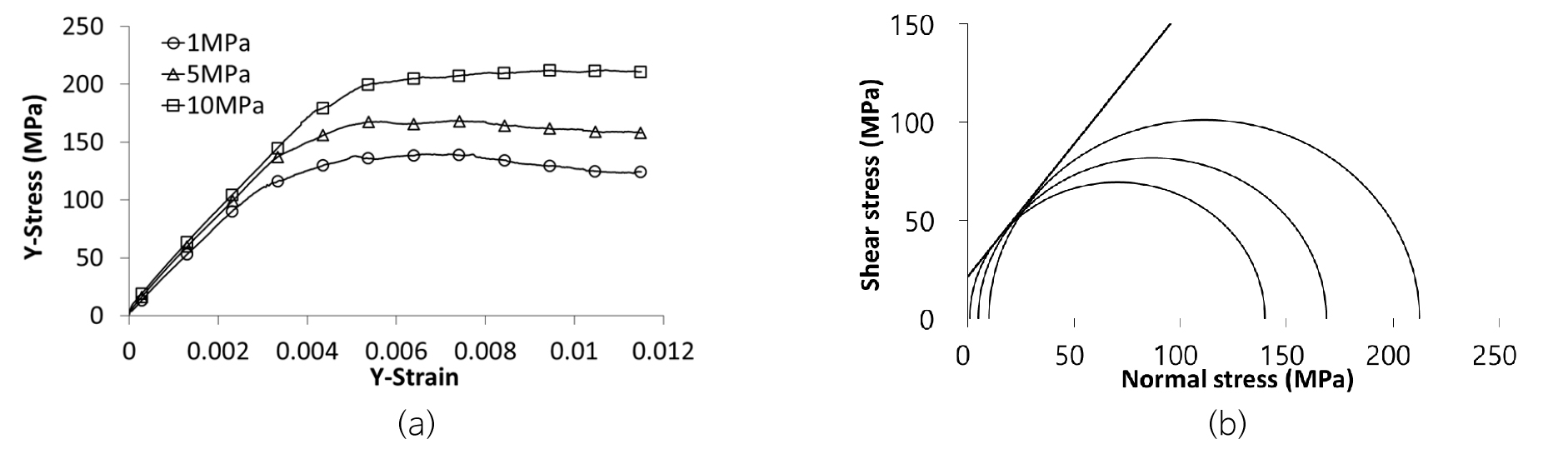
Fig. 7a는 3.4 m 큐브에서 y 방향으로 재하에 따른 응력-변형 관계를 보여주는데, 추정된 블록강도 및 변형계수는 각각 139.74 MPa 및 38.21 GPa이다. 여기서, 변형계수는 최대 블록강도의 50%에서 접선계수로 추정된 값이다. 또한, x, z 방향의 수직 경계면에서 기록된 변위 자료로부터 포아송비가 산정되었다(Fig. 7b & 7c). x, y, z 각 방향으로의 응력-변형 해석은 구속압을 증가시키면서 각각 3회에 걸쳐 수행되었으며 구속압에 따라 결정된 최대 블록강도 값으로부터 Mohr-Coulomb 파괴 포락선을 작도하고 큐브 블록의 x, y, z 방향에 따른 지향적 점착력과 마찰각이 결정되었다. Fig. 8은 3.4 m 큐브에 대하여 구속압이 1 MPa, 5 MPa, 10 MPa일 때 y 방향으로의 응력-변형 관계와 각각의 최대 블록강도 값에 의해 작도된 Mohr-Coulomb 파괴 포락선을 보여준다.
신선암의 전단탄성계수(G) 및 체적탄성계수(K)는 각각 식 (1) 및 식 (2)를 통하여 산정할 수 있다.
여기서, E와 ν는 탄성 등방의 신선암인 경우에 유효하다. 절리의 기하학적 속성에 기인한 이방성을 갖는 DFN 블록의 전단탄성계수 및 체적탄성계수는 DFN 큐브 블록에 대한 응력경로를 설정하고 수치해석을 통하여 추정할 수 있다. 본 연구는 Fig. 9와 같이 응력경로를 설정하고 3DEC 해석을 통하여 전단탄성계수 및 체적탄성계수를 추정하였다. 전단탄성계수 추정을 위한 응력경로는 큐브 블록에 대하여 직교하는 x, y, z 방향으로 1 MPa의 구속압을 유지하고 큐브 블록에 대한 전단응력을 증가시키는 방식이다. 전단응력의 증가에 따라 큐브의 경계면에 설정된 9개 모니터링 포인트에 기록된 변위로부터 전단탄성계수 Gxy, Gyz, Gxz가 결정되었다. Fig. 9b는 DFN 시스템의 체적탄성계수 추정을 위한 응력경로이다. 체적탄성계수는 DFN 큐브 블록에 대하여 직교하는 x, y, z 방향으로 압축응력을 가할 때 발생하는 블록 체적의 감소를 산정하고 압축응력에 따른 블록 체적의 변화로부터 결정하였다. 체적탄성계수는 블록에서 서로 다른 방향이나 면에 무관한 블록의 삼차원 파라미터이다.
결과 및 토의
개별체 기반의 수치해석을 통하여 연구지역에서 추정된 DFN 큐브 블록의 지향적 강도 및 변형 파라미터가 Table 4, Table 5, Table 6에 수록되어 있다. DFN 시스템의 최대 블록강도(Si)는 3.4 m 큐브에서 x, y, z 방향에 따라 116.86~164.22 MPa 범위의 뚜렷한 직교이방성을 갖는 것으로 평가되었다. DFN 큐브 블록의 크기가 7.2 m, 15 m로 증가함에 따라 최대 블록강도는 감소하는 양상이며 z 방향에서 가장 많이 감소하였다. DFN 블록의 변형계수(Emi), 전단탄성계수(Gjk), 체적탄성계수(Km), 마찰각, 점착력 등의 강도정수도 방향에 따른 변동성을 보이며 큐브의 크기가 증가함에 따라 감소하는 양상을 확인할 수 있다. 이와 같이 DFN 시스템의 강도 및 변형 특성은 뚜렷한 역학적 이방성을 도출하였는데, 이는 절리의 방향분포를 비롯한 기하학적 속성에 의한 영향으로 판단된다.
Table 4.
Estimated values of strength and deformability parameters in the x, y, and z directions for cubic blocks of various size
Table 5.
Estimated Poisson’s ratios for cubic blocks of various size
Table 6.
Estimated shear modulus and bulk modulus for cubic blocks of various size
|
Block size (m cube) | Shear moduli (GPa) |
Bulk modulus (GPa) Km | ||
| Gxy | Gyz | Gxz | ||
| 3.4 | 16.38 | 17.16 | 16.14 | 29.16 |
| 7.2 | 15.47 | 14.99 | 15.12 | 27.98 |
| 15.0 | 14.17 | 14.11 | 14.92 | 26.85 |
Fig. 10은 DFN 블록의 강도 및 변형 특성에 대한 신선암 대비 저감률(reduction factor)를 그래프에 나타낸 것이다. Fig. 10a는 x, y, z 방향으로 DFN 블록의 크기가 블록강도에 미치는 영향을 보여준다. 여기서, 세로축은 수치해석을 통해 i 방향으로 산정된 지향적 최대 블록강도 Si를 신선암의 일축압축강도 qu로 나누어 정규화한 무차원 변수이다. 또한, Fig. 10b~10d는 x, y, z 방향으로 DFN 큐브 블록의 크기가 정규화한 블록변형특성에 미치는 영향을 보여준다. 여기서 Emi, Gjk는 각각 i 방향의 블록변형계수, jk방향의 전단탄성계수이다. Fig. 10의 결과는 블록강도, 변형계수, 전단탄성계수, 체적탄성계수 모두 DFN 큐브 블록 크기의 증가에 따라 값이 감소하여 일정 값에 수렴함을 지시한다. 7.2 m 큐브의 블록강도는 x, y, z 방향으로 신선암 대비 각각 51.4%, 51.6%, 62.8%로 감소하였다. 신선암 대비 블록변형계수는 x, y, z 방향으로 각각 63.3%, 63.4%, 53.8%로 나타났으며 전단탄성계수는 xy, yz, zx 면에서 각각 69.8%, 67.6%, 68.2% 수준으로 감소하였다. 또한, 체적탄성계수는 신선암의 61.6%로 감소하였다. 15 m 큐브에서도 블록의 강도 및 변형 파라미터는 7.2 m 큐브의 파라미터 값과 거의 유사하게 산정되었다. 이와 같은 결과는 현장의 백악기 흑운모 화강암 암반의 역학적 특성에 대한 대표요소체적(representative elementary volume, REV) 크기로 7.2 m 큐브 이상이 적합할 수 있음을 지시하며 본 연구는 보수적으로 15 m 큐브를 REV로 결정하였다.
본 연구에서 개별체 수치해석을 통하여 추정한 절리성 암반의 강도정수는 사례현장에 대한 삼차원 구성모델 도출에 활용할 수 있다. 선형-탄성의 직교이방성을 띠는 절리성 암반에 대한 파괴 전 거동을 설명하는 구성모델은 식 (3)과 같다.
현장의 역학적 REV 크기 이상인 15 m 큐브에서 결정된 변형 파라미터 값(Tables 4, 5, 6)을 식 (3)에 대입하면 연구지역의 백악기 흑운모 화강암 암반에 대한 구성모델을 수립할 수 있는데, 도출된 식 (4)는 사례현장의 절리분포에 의한 암반의 직교이방적 거동을 고려할 수 있다.
여기서, 와 는 각각 수직변형률 및 전단변형률의 증분이며 와 는 각각 수직응력 및 전단응력의 증분이다.
본 연구에서 유한크기의 절리로 이루어진 DFN 큐브 블록에 대한 3DEC 기반의 응력-변형 해석을 위하여 생성된 다면체 개별요소는 가상절리와 유한 길이의 실제절리가 연결되어 생성되었다. 가상절리의 도입으로 인하여 가상절리와 실제절리가 교차하는 부분에서 응력이 집중될 가능성도 있다. 본 연구는 이와 같은 국부적 응력집중을 해소하는 방편으로 실제절리의 경사가 45° 이하인 경우 수직 가상절리를 연결하였으며 45°보다 큰 경사의 실제절리에 대해서는 수평 가상절리를 도입하였다. 국부적 응력집중에 의한 효과가 유의미할수록 Fig. 10의 블록크기에 따른 응력 및 변형 파라미터 값은 오르내림 변동을 보일 가능성이 크지만 추정된 모든 파라미터 값은 점진적 하향을 나타내고 있다. 이러한 수치해석 결과는 블록의 역학적 특성에 미치는 절리 기하특성의 영향에 비해 국부 응력집중의 영향이 무시될 수 있음을 의미한다.
현장의 절리성 암반에 대한 역학적 REV 결정 및 강도정수 추정은 현재에도 매우 도전적인 과제이다. 본 연구는 현장적용 사례를 통하여 절리성 암반에 대한 개별체 수치해석 기반의 응력-변형 해석을 위한 절차를 제시하였지만, 절리의 역학적 조건의 단순화와 관련된 한계도 있다. 본 연구의 구성모델은 해석영역에 분포하는 세 절리군의 역학적 특성이 서로 같다는 가정하에 도출된 것이다. 따라서 지질공학 프로젝트 수행을 위해 본 연구의 작업흐름을 적용하는 경우 입력변수에 대한 세심한 검토가 뒷받침되어야 한다. 예로서 절리마찰각, 절리점착력, JKN, JKS 등의 역학적 특성은 절리군별로 실내실험을 통해 측정된 값을 사용해야 한다. 또한, 특정 절리군에서 역학적 특성의 변동성이 유의미하다고 판단되면 이에 대한 고려가 해석에 충분히 반영되어야 한다.
결 론
본 연구는 부산 기장지역에 분포하는 백악기 흑운모 화강암 암반에 대하여 개별체 수치해석을 통한 응력-변형 해석을 수행하고 절리성 암반의 강도 및 변형 특성을 평가하였다. 절리성 암반의 역학적 특성에 대한 규모효과와 REV를 규명하기 위하여 제시된 연구절차는 절리의 기하학적 특성에 따른 절리성 암반의 역학적 이방성을 고려할 수 있으며 암반의 강도 및 변형 파라미터 추정에 사용할 수 있다. 연구지역의 결정질 절리성 암반에 대한 역학적 REV의 크기는 15 m 큐브로 결정되었으며, x, y, z 방향에서 산정된 강도 및 변형 파라미터값을 평균하였을 때 REV의 블록강도 및 변형계수는 각각 신선암의 52.8% 및 57.7%로 평가되었다. 이는 절리의 기하학적 속성에 의한 절리성 암반에 대한 역학적 특성의 저하를 정량적으로 지시한다.
세 개의 절리군을 포함하는 연구지역에서 세 절리군 모두 절리의 역학적 특성이 동일하다는 가정 하에 절리성 암반에 대한 파괴 전 거동을 설명하기 위한 선형-탄성 직교이방성 구성모델이 도출되었다. 본 연구의 작업흐름을 실제 지질공학 과업 수행에 적용하기 위해서는 절리마찰각, 절리점착력, JKN, JKS 등의 역학적 특성이 절리군별 개별적으로 평가되어야한다. 또한, 현지응력 측정을 통하여 주응력의 크기 및 방향과 같은 경계조건의 설정도 필요하다.