서 론
계단상 활동 파괴의 한계 평형 해석
절리 간격/길이 비와 암교의 임계인장강도
계단 경로 파괴 평가 절차: 경주 덕동호 사면 사례
체계적 불연속면 조사와 운동학적 해석
계단 경로 파괴면의 구성과 한계 평형 해석
토의 및 결론
서 론
대규모 절리 암반 사면에서 사면을 관통하는 불연속면이 존재하지 않아도 계단상 활동면에 의한 파괴가 발생할 수 있다(Huang et al., 2015). 이러한 계단상 활동면은 비연속성 절리계(non-persistent joint system)의 분포 특성에 기인한다. 일정한 자세를 가지는 하나의 절리군에서 불연속면의 분포 특성은 Fig. 1a와 같이 절리의 연속성(persistence) 또는 2차원 단면에서 절리 길이(joint length, L)와 각 절리 간의 거리로 정의된다(ISRM, 1978; Priest and Hudson, 1981). 여기서는 각 절리간의 거리를 개별 절리 간의 거리를 평행한 두 절리 사이의 법선 거리인 절리 간격(joint spacing, S)과 동일 평면 상에 놓인 두 절리 사이의 거리인 절리 이격(joint gap, G)으로 구분하였다.
절리 암반 사면에서 계단상의 활동면은 절리-절리(joint-to-joint) 활동면 또는 절리-암교(joint-to-rock bridge) 활동면으로 형성된다(Einstein, 1993). Fig. 1b의 계단상 활동면에서 절리-절리 활동면은 경사각 θ1, θ2를 가지는 J1 및 J2 절리군의 절리가 연결되어 형성된다. 최소한 하나의 절리군 경사각은 사면 경사각(ψ) 보다 작아야 하며, 상대적으로 낮은 경사각 θ1을 가지는 J1 절리군이 활동 유효면(effective surface)이 된다(Kovari and Fritz, 1978).
Fig. 1b에서 절리-암교 활동면은 절리부와 암교부의 연결로 형성되며, 암교는 두 절리 사이를 연결하는 파괴면 상의 암석부로 암교각(rock bridge angle)은 활동 유효면을 이루는 J1 절리와 암교가 이루는 각이다(Zhang et al., 2020). 임의의 암교각 β를 가지는 암교 길이 RBL은 J1 절리에 수직한 절리 간격 성분인 RBL(S)와 절리에 평행한 절리 이격 성분인 RBL(G)로 그 성분을 나눌 수 있다. Fig. 1b에서 절리 길이 JL과 암교 길이 RBL로 구성된 계단 경로 파괴(step-path failure)면은 활동 암괴의 하중 W에 의해 암교가 파괴되며 암교 양단의 두 절리가 연결되어 발생한다.

Fig. 1.
Stepped sliding surfaces in a jointed rock slope. a) geometrical parameters of discontinuities, b) step-path failure of the rock slope. ψ: dip angle of slope; W, weight of sliding block; θ1 and θ2: dip angles of the J1 and J2 joint sets; JL and RBL, joint length and rock bridge length on the step-path failure surface, respectively; β, rock bridge angle as the angle between rock bridge and joint; RBL(S) and RBL(G), rock bridge length normal (joint spacing component) and parallel (joint gap component) to J1 joint set, respectively.
계단 경로 파괴 해석을 위하여 다양한 한계 평형 해석법(Jennings, 1970; Jaeger, 1971; Kovari and Fritz, 1978; Einstein et al., 1983; Yoon et al., 2000)이 제시되었으며, 최근에는 파괴역학 개념의 수치 해석적 또는 실험적 연구가 적극적으로 이루어지고 있다(Eberhardt et al., 2004; Stead et al., 2006; Huang et al., 2015). 여기서는 계단 경로 파괴에 대한 한계 평형 해석 기법을 소개하고, 이에 대한 절리 간격 및 길이 등 불연속면 분포 특성의 영향을 분석하였다. 또한 사례를 통하여 대규모 암반 사면의 계단 경로 파괴 평가에 적용할 수 있는 조사 및 해석 절차를 검토하였다.
계단상 활동 파괴의 한계 평형 해석
암반 사면의 활동 파괴에 대한 안정성은 활동 암괴의 하중(W)에 의한 활동력(driving force)과 이에 대한 저항(resistance)의 비로 정의되는 안전율(factor of safety) 또는 그 차로 정의되는 안전 경계(safety margin)로 분석할 수 있다. 절리 길이 JL과 절리 경사각 θ를 가지는 관통상의 단일 절리 활동면(single joint sliding surface, Fig. 2a)에 대한 건조 상태의 2차원 암반 사면의 안전율 FS는 식 (1)로 계산된다(Hoek and Bray, 1981). 식 (1)에서 cj, øj는 절리의 점착력 및 마찰각이며, 활동면의 길이 A는 활동면을 이루는 절리의 길이 JL과 동일하다.
제한된 연장성을 가지는 두 개 이상의 절리군이 암반 사면에 발달할 때, 절리군 간의 상호 교차에 의해 계단상 활동면이 형성될 수 있다. Kovari and Fritz(1978)는 Fig. 2b와 같이 인장 강도가 0이고, 경사각 θ1, θ2를 가지는 J1, J2 절리군에 의해 형성된 계단상 활동면에 대하여 경사각 θ1을 가지는 J1 절리군에 의해 형성된 유효면의 길이 A를 경사각 θ′을 가지는 평균면(mean surface)의 길이 A′를 이용하여 식 (2)와 같이 정의하였으며, 이를 식 (1)에 대입하여 안전율을 구할 수 있다.
Jennings(1970)는 Fig. 2c와 같이 동일 평면(in-plane condition) 상에 존재하는 절리-암교 활동면을 가정하였으며, 이 활동면의 길이 A는 절리 길이 JL과 절리 이격 성분 암교 길이 RBL(G)의 합이다. Jennings(1970)의 절리 연장성 요소(joint persistent factor) K는 식 (3)과 같이 활동면 길이 A에 대한 절리 길이 합의 비로 정의되며, 식 (4)에서 절리 연장성 요소를 이용하여 활동 암괴의 하중 W에 대한 안전율을 구할 수 있다. 이때, cj, øj와 cr, ør는 각각 경사각 θ를 가지는 절리와 암교의 점착력과 마찰각이다.
Jaeger(1971)는 Fig. 2d와 같이 경사각 θ를 가지는 절리들이 절리 양단에서 활동암괴의 하중 W에 의해 절리면에 직각인 인장 파괴가 발생하여 연결(on-lap condition)되는 절리-암교 활동면을 가정하였다. 식 (5)는 이러한 조건에서 활동 암괴의 하중 W에 대하여 경사각 θ′과 길이 A′을 가지는 평균면(mean surface)을 활동면으로 하여 안전율을 계산하는 식으로 제시된 것이며, c, ø, Tr은 각각 활동면의 점착력과 마찰각, 암교의 인장강도이다.
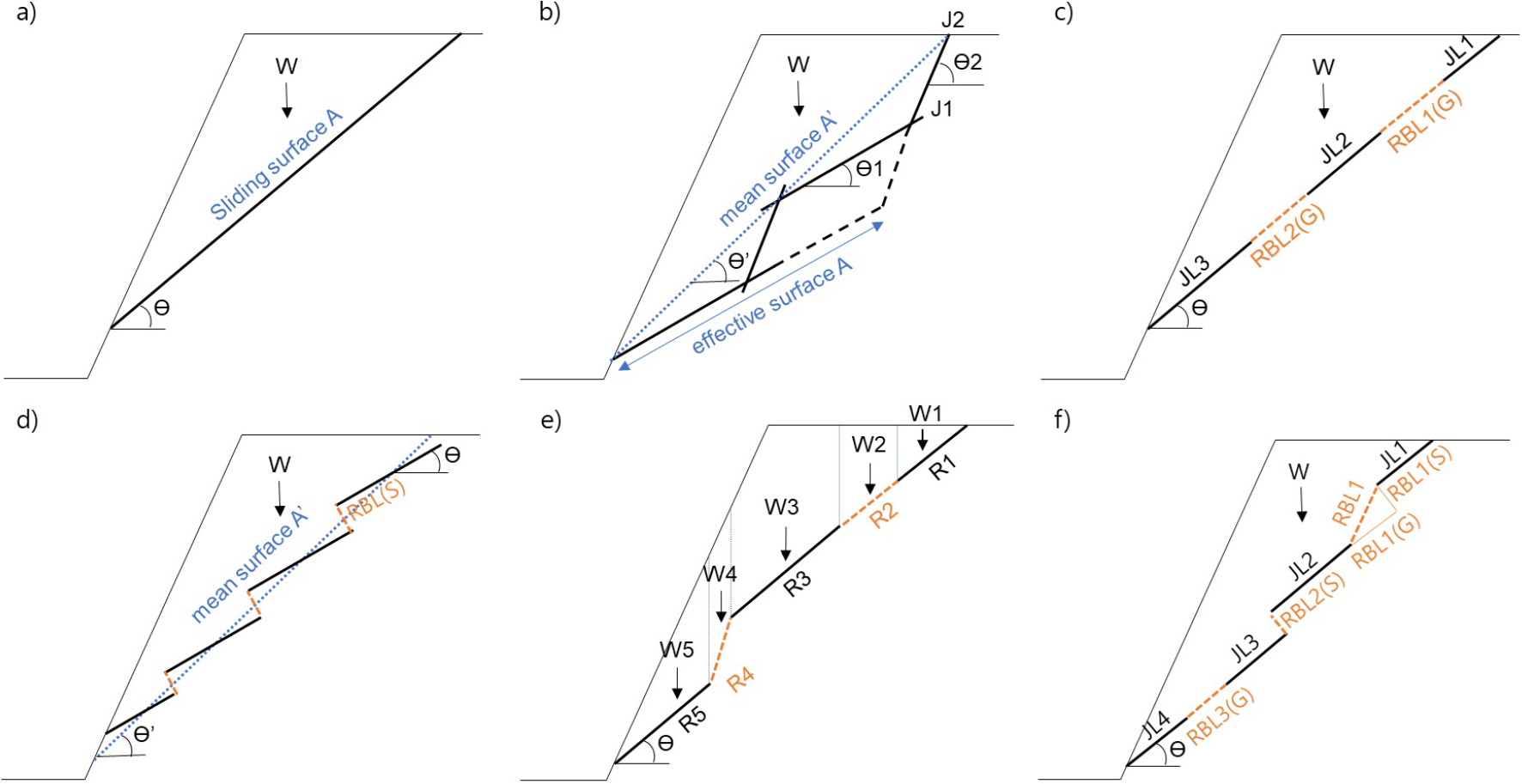
Fig. 2.
2D safety analysis models for a jointed rock slope. a) single joint sliding surface (after Hoek and Bray, 1981); b) joint-to-joint sliding surface, modified from Kovari and Fritz (1978), c)~f) joint-to-rock bridge sliding surface modified from Jennings (1970), Jaeger (1971), Einstein et al. (1983) and Yoon et al. (2000). Wn and Rn, weight and resistance of nth slice, respectively; θ and θ′, dip angles of A and A′, respectively; JLn and RBLn, lengths of nth joints and rock bridges, respectively. For key to other abbreviations, see Fig. 1.
Einstein et al.(1983)은 암교의 파괴에서 활동 암괴 하중에 의한 인장 균열의 발생을 주요 원인으로 보고, 발생한 인장 균열이 활동 유효면인 절리면과 이루는 각 θt가 암교각 β와 이루는 각관계에 따라 암교가 유효 활동 절리면과 동일 평면이거나 저각의 암교각으로 형성되는 경우(β<θt)와 고각의 암교각을 이루는 경우(β>θt)로 구분하였다. 전자의 조건에서 식 (6)과 같이 절리 이격 성분 암교 길이 RBL(G)와 암석의 전단강도 τr에 의한 암교 전단저항 Rrs, 후자의 조건에서는 식 (7)과 같이 절리 간격 성분 암교 길이 RBL(S)와 암석의 인장강도 Tr에 의한 암교 인장저항 Rrt를 정의하였다. 이에 따라 Fig. 3e와 같이 경사각 θ를 가지는 절리들과 임의의 암교각을 가지는 암교로 이루어진 계단상 활동면에서 활동 암괴를 활동면의 개별 절리부(JL)와 암교부(RBL)에 의해 구분되는 절편으로 분리하여 식 (8)과 같이 각 절편의 하중 Wi와 저항 Ri에 따른 안전 경계 SMi를 구하고 이를 합하여 안전경계 SM을 구하였다. 이 때 각 절편의 저항 Ri는 절리 절편의 경우 절리의 전단저항 Rjs, 암교 절편일 경우 암교각 β에 따라 식 (6) 또는 식 (7)에 의하여 구하여지는 암교의 전단 및 인장저항 Rrt이다.
Yoon et al.(2000)은 Fig. 2f와 같이 경사각 θ의 활동 유효면을 이루는 절리면들과 임의의 암교각을 가지는 암교들로 구성된 계단상 활동면에 대해 그 총 저항을 암교의 절리 간격 성분 길이 RBL(S)와 암석 인장강도 Tr에 의한 암교 인장저항 Rrt, 암교의 절리 이격 성분 길이 RBL(G)와 암석 전단강도에 의한 암교 전단저항 Rrs, 절리면 길이 JL과 절리 전단강도에 의해 결정되는 절리 전단저항 Rjs로 구분하였다. 각각의 저항은 식 (9), (10), (11)로 정의되며, cj, øj와 cr, ør은 각각 절리와 암교의 점착력과 마찰각이다. Fig. 2f에서 계단상 활동면의 총 저항은 Rrt, Rrs, Rjs의 합이며 활동 암괴의 하중이 W일 때, 계단 경로 파괴면의 안전율은 식 (12)로 구할 수 있다.
Yoon et al.(2000)의 계단 경로 파괴 모델은 절리의 양단에서 윙 크랙(wing crack)과 같이 절리와 직각으로 형성되는 인장 균열에 의해 두 절리가 연결되는 것을 가정한 모델로서 절리의 간격이 절리의 길이에 비해 충분히 작을 때 효과적으로 적용될 수 있다. 만약 두 절리 사이에서 인장 균열이 하중 방향과 평행하게 수직으로 발생하는 것을 고려해야 한다면 Einstein et al.(1983)의 인장균열 각 θt가 암교각 β와 이루는 각관계에 따라 식 (10)의 암교 전단저항 Rrs은 절리 이격 성분 암교 길이 RBL(G)를 RBL(G) - (RBL(S)/tanθt)로 대체하여 구할 수 있다.
또한 Fig. 2f에서는 활동 유효면을 이루는 하나의 절리군이 암교와 연결되는 계단 경로 파괴면을 제시하고 있으나, Fig. 1b와 같이 활동 유효면을 이루는 하나의 절리군 J1 이외에 이보다 급한 경사의 절리군 J2가 함께 발달하여 절리-절리 활동면과 절리-암교 활동면이 복합적으로 연결된 계단 경로 파괴면이 형성될 수 있다. 이 경우, 계단 경로 파괴면 상에 놓이는 J2 절리군의 길이는 절리의 인장저항을 제공한다. 일반적으로 절리의 인장강도는 0이므로 J2 절리군에 의한 인장저항 역시 0이 되기 때문에 계단상 활동면의 총 저항에 영향을 미치지 않으나, J2 절리의 인장강도가 유의미하게 존재한다면 절리 인장저항을 고려할 수 있다. 이 경우, J2 절리의 인장강도 Tj와 J2 절리의 J1 절리 간격 성분 길이 JL(S)를 이용하여 식 (13)에 의해 J2 절리군에 의한 절리 인장저항 Rjt를 구할 수 있다. 이때, 계단 경로 파괴면의 총 저항은 암교와 절리 각각의 인장저항과 전단저항인 Rrt, Rrs, Rjt 및 Rjs의 합이다.
절리 간격/길이 비와 암교의 임계인장강도
절리의 전단강도에 비해 암교의 전단강도 및 인장강도가 크므로 절리부와 암교부가 동일한 길이라면 Yoon et al.(2000)의 식 (12)에서 암교가 절리-암교 활동면에 보다 큰 저항을 제공한다. 따라서 동일한 길이의 계단상 활동면에서 암교부 길이(ΣRBL)의 비중이 커질수록 총 저항은 증가한다. 또한 암석의 인장강도는 일반적으로 점착력의 1/2 이하로 평가되므로 동일한 암교 길이에서 암교 인장저항과 관련된 RBL(S)가 암교 전단저항과 관련된 RBL(G)보다 크면 클수록 계단 경로 파괴의 가능성이 높아진다. 즉, 절리와 직각(β = 90°) 또는 암교각이 고각(β > θt)인 암교가 절리와 평행(β = 0°) 또는 암교각이 저각(β < θt)인 암교에 비해 계단 경로 파괴에 취약하다.
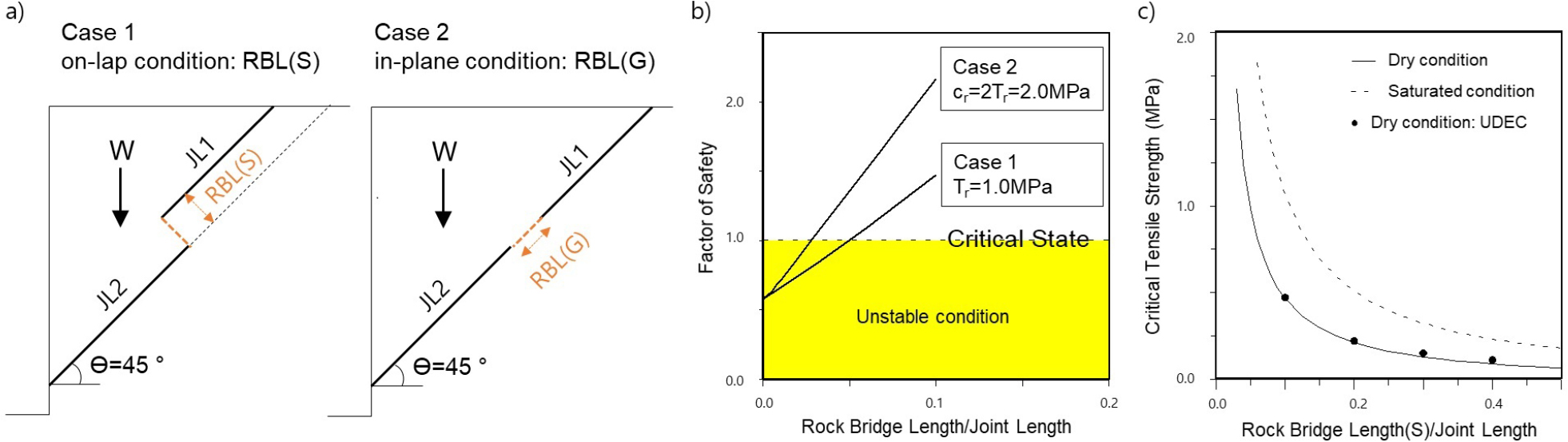
45°의 경사각을 가지는 두 개의 절리가 암교로 연결되는 Fig. 3a의 예제 사면에서 Case 1(on-lap condition)은 암교각이 직각인 길이 RBL(S)의 암교가 인장저항을 제공하고, Case 2(in-plane condition)는 절리면과 동일 평면상으로 형성된 길이 RBL(G)의 암교가 전단저항을 제공한다. Fig. 3b는 식 (12)를 이용하여 건조 조건의 예제 사면에 대한 안전율 분석한 결과로서 입력값은 암석의 단위 중량 2,500 kg/m3, 인장강도 1.0 MPa, 점착력 2.0 MPa, 마찰각 30°, 절리의 인장강도와 점착력은 각각 0, 마찰각 30°이다. Case 1에서는 ΣRBL(S)/ΣJL의 비가 0.05 이하가 되면 안전율 1.0 이하가 되며, Case 2에서는 ΣRBL(G)/ΣJL 비가 0.02 이하가 되어야 안전율 1.0 이하의 불안정상태에 도달한다. 즉, 동일한 암교 길이/절리 길이 비에서 Case 1이 파괴에 취약하다. 이러한 결과는 ΣRBL(S)/ΣJL 비가 계단 경로 파괴에 가장 큰 영향을 주고 있음을 지시하며, 이에 대응하는 절리 분포 특성은 절리 간격/길이의 비로서 Zhang et al.(2020)은 이를 절리 간격 요소(joint spacing factor) d로 명명한 바 있다.
Fig. 3c은 암교각이 90°인 Case 1에서 ΣRBL(S)/ΣJL 비를 변화시키며, 안전율이 1.0이 되는 암석의 임계인장강도(critical tensile strength, Tc)를 식 (12)에서 도출된 식 (14)로 계산하고 UDEC 코드(ITASCA, 1996)로 수치 해석하여 비교한 결과이다. 암교의 임계인장강도는 ΣRBL(S)/ΣJL 비가 감소할수록 지수함수적으로 증가하며, ΣRBL(S)/ΣJL 비가 0.05일 때 건조 조건에서 임계인장강도가 1.0 MPa인 반면, 포화 조건에서는 2.0 MPa을 크게 상회한다. 따라서 비연속성 절리가 발달하는 암반 사면에서 암석 인장강도가 1.0 MPa일 때, ΣRBL(S)/ΣJL 비에 대응하는 절리 간격/길이의 비가 0.05 이하라면 계단 경로 파괴의 위험성이 급격히 커진다.
계단 경로 파괴 평가 절차: 경주 덕동호 사면 사례
체계적 불연속면 조사와 운동학적 해석
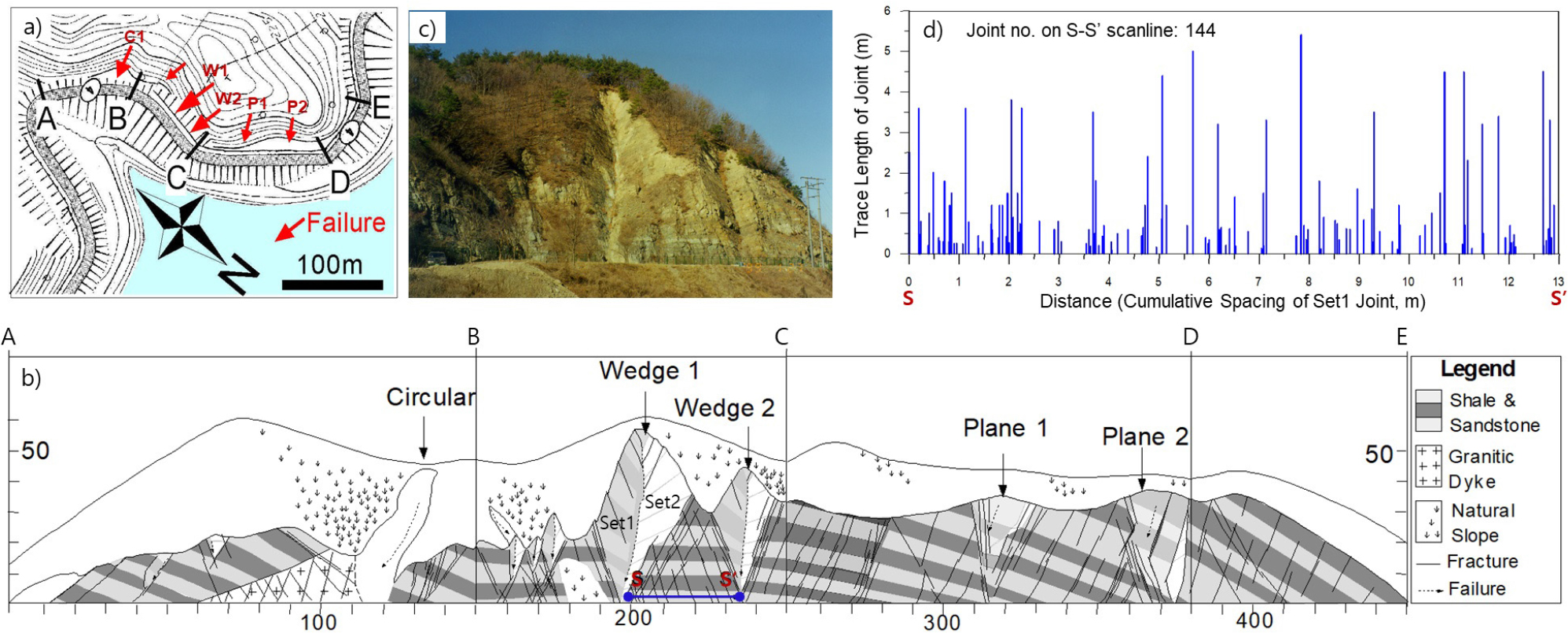
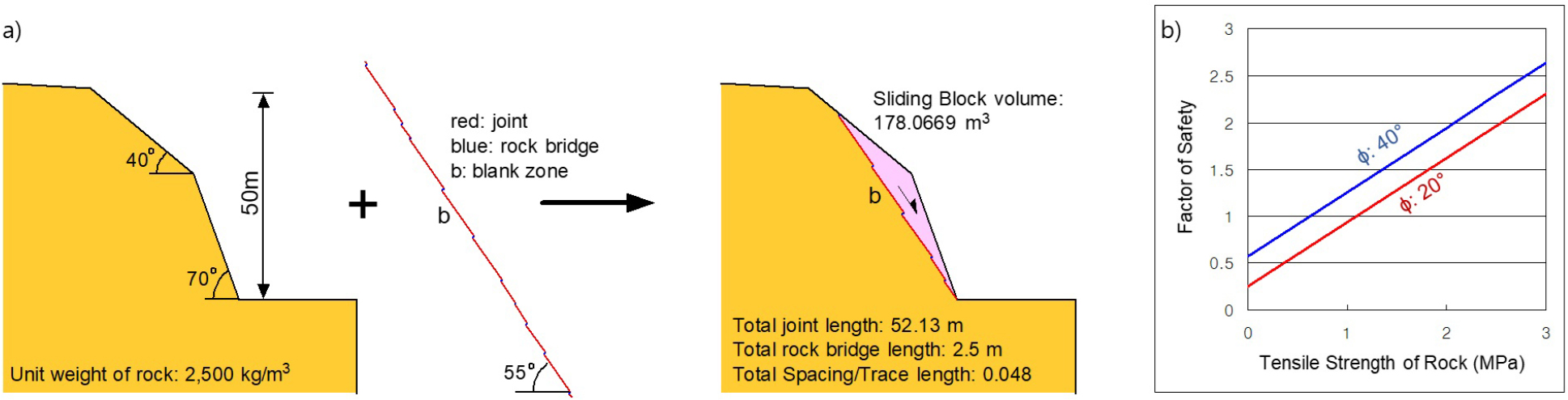
경상북도 경주 덕동호 주변 도로 사면(Fig. 4a)을 대상으로 계단 경로 파괴 평가를 수행하였다. 대상 사면은 백악기 퇴적암과 이를 관입하는 화강암이 분포하며, 다수의 활동 파괴가 발생하였다(Fig. 4b). 백악기 퇴적암이 분포하는 Fig. 4c의 B-C 구간 사면 Slope B-C에서 W1과 W2의 대규모 쐐기 파괴가 발생하였으며, 두 파괴 지점 사이에서 약 35 m 길이의 선조사(scanline survey)가 수행되었다. 이 쐐기를 이루는 좌측(남서부) 활동면을 이루는 절리군을 Set 1, 우측(북서부) 활동면을 이루는 절리군을 Set 2로 구분하였으며, 각 활동면은 비연속성 절리면들이 계단상을 이루어 구성되어 있다. Set 1 절리 간격으로 환산된 조사선 S-S′의 길이는 약 13 m이며, Fig. 4d에서 이 조사선과 교차하는 Set 1 절리의 위치와 길이를 도시하였다.
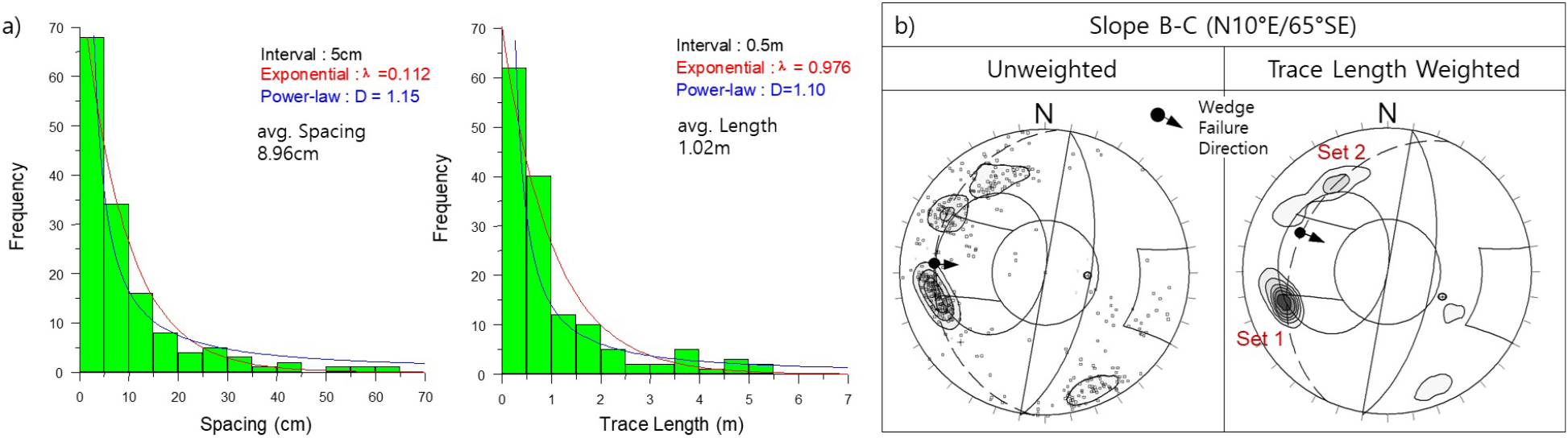
조사선 S-S′에서 확인된 Set 1 절리의 간격과 길이에 대한 확률밀도분포는 Fig. 5a와 같다. 절리의 간격과 길이 모두 음의 지수 분포를 보이고 있으며, 평균값은 간격 9.0 cm, 길이 1.0 m로 평균 절리 간격/길이의 비는 0.09이다. Fig. 5b는 선조사에서 측정한 절리의 방향을 평사투영망에 도시하여 운동학적 해석을 수행한 결과이다. 가중치를 적용하지 않은 평사투영해석에서 Set 1 절리와 Set 2 절리에 의한 쐐기 파괴는 발생하지 않거나 얕은 깊이로 발생하는 것으로 평가되어 실제 발생한 깊은 쐐기 파괴의 특징을 반영하고 있지 못하다. 반면 절리 길이를 가중치로 적용한 평사투영해석에서는 대규모로 발생한 쐐기 파괴의 형상을 잘 반영하고 있어 절리의 길이가 쐐기 파괴의 발생에 큰 영향을 주고 있음을 확인할 수 있다. 이는 사면의 평사투영 해석에서 절리 길이를 가중하여 평가하는 방법이 비연속성 절리가 발달하는 암반 사면의 운동학적 평가에 보다 효과적인 분석 방법임을 보여준다.
계단 경로 파괴면의 구성과 한계 평형 해석
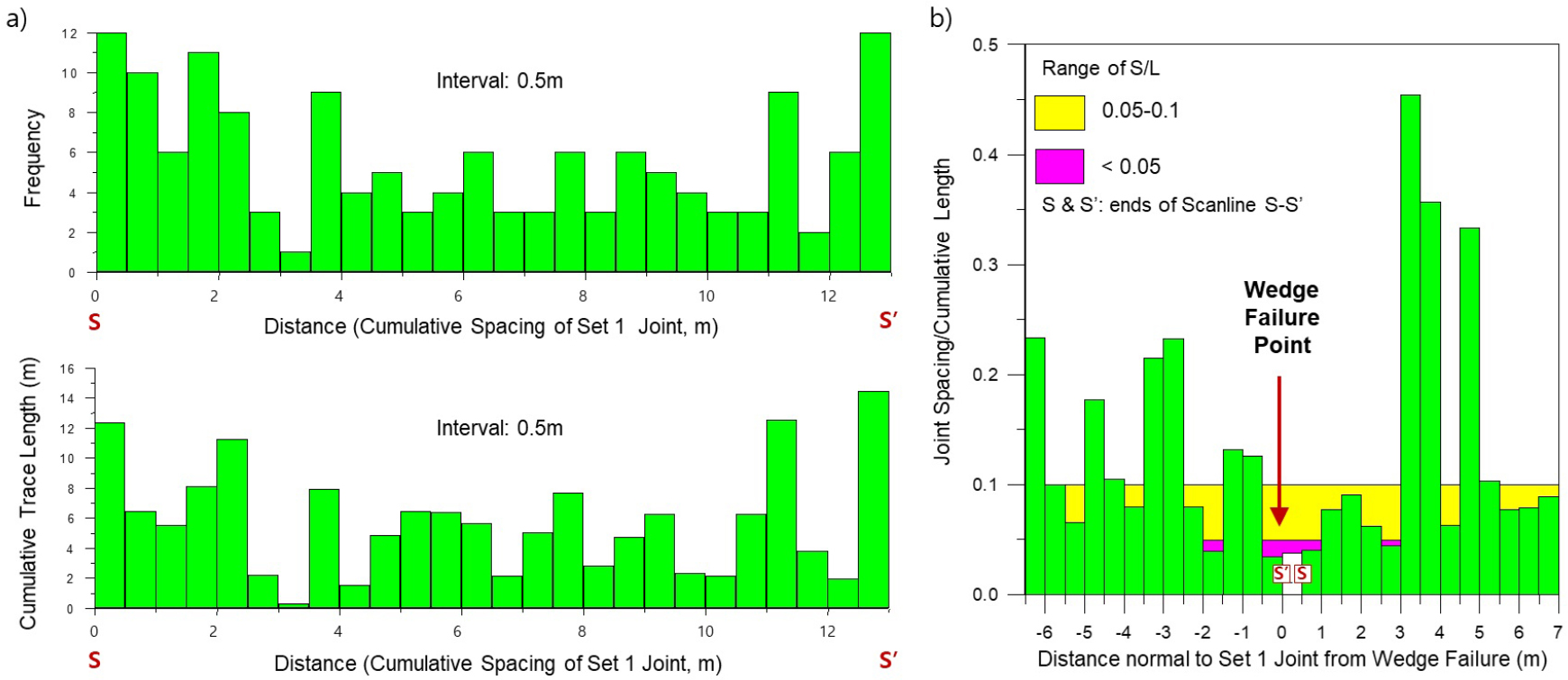
Fig. 6a는 조사선 S-S′에서 0.5 m 간격으로 Set 1 절리 빈도와 누적 길이를 분석한 것으로 파괴 지점에 인접한 조사선 양단에서 절리 빈도와 누적 길이가 급증한다. Fig. 6b는 0.5 m 구간별로 절리 빈도의 역수인 평균 절리 간격과 누적 길이의 비를 파괴 지점을 기준으로 재배열한 것으로, 조사선 S-S′의 양단인 S 및 S′ 지점은 파괴 지점 및 그와 인접한 위치에 해당한다. Fig. 6b에서 파괴 지점을 중심으로 -2~+3 m 범위에서 절리 간격/누적 길이의 비가 0.05 이하인 구간이 집중되어 있으며, 쐐기 파괴는 절리 간격/길이의 비가 최소인 구간에서 발생하였다.
Fig. 7a는 Fig. 6a의 구간별 평균 절리 간격과 누적 길이를 이용하여 2차원 단면에서 겉보기 경사각 55°를 가지는 Set 1 절리에 의한 계단-경로 파괴면을 on-lap조건을 가정하여 구성한 것이다. 구성된 파괴면에서 절리부 길이의 합 ΣJL는 52.1 m, 이에 직교하는 암교부 길이 ΣRBL(S)는 2.5 m로서 ΣRBL(S)/ΣJL 비는 0.048이다. Fig. 7b는 암석 단위중량이 2,500 kg/m3일 때, 허용 안전율에 따른 건조 상태의 암교의 임계인장강도를 식 (14)로 구한 것이다. Fig. 7b에서 허용 안전율이 1.0일 때, 점착력 0인 절리의 마찰각이 20~40°의 범위라면 0.5~1.0 MPa의 인장 강도를 가진 암교의 파괴로 계단 경로 파괴가 발생할 수 있다. 또한 계단상 활동면 중 일부가 절리-절리 활동면이거나 포화 상태 또는 1.0 이상의 안전율을 고려한다면 암석의 인장강도가 1.0 MPa 이상일 경우라도 사면은 불안정한 상태로 평가될 수 있다.
토의 및 결론
비연속성의 절리를 가지는 암반 사면에서 절리-절리 활동면 또는 절리-암교 활동면에 의한 계단 경로 파괴가 발생할 수 있다. 계단 경로 파괴면의 주된 저항은 절리에 비해 전단 및 인장강도가 큰 암교의 저항에서 비롯되므로 계단 상 활동면에서 암교 길이/절리 길이의 비가 작을수록 파괴에 취약하다. 또한 암석의 인장강도는 전단강도에 비해 낮으므로, 동일한 길이를 가지는 암교에서 암교각이 90° 또는 고각일 때 저각일 경우에 비해 계단 경로 파괴에 취약하다. 따라서 계단 경로 파괴의 가능성은 절리 간격/길이의 비가 작을수록 높아지며, 암석의 인장강도가 1 MPa일 때, 절리 간격/길이의 비가 0.05 이하라면 파괴 가능성이 높으므로 주의하여야 한다.
예시한 인장강도 1 MPa인 암석은 신선암을 기준으로 할 때 연약한 암석(soft rock)에 해당하기 때문에 인장강도가 큰 암석의 경우 계단 경로 파괴의 가능성은 축소된다. 암석의 인장강도는 일반적으로 일축압축강도의 1/33~1/4, 점착력의 1/6~1/2, 점하중강도의 0.8~1.5의 값으로 알려져 있다(Hoek and Brown, 1997; Sheorey, 1997; Perras and Diederichs, 2014). 이를 고려하면 인장강도 1 MPa 이하의 암석은 대체로 ISRM(1978)의 일축압축강도 5~25 MPa를 가지는 R2 등급의 약한 암석(weak rock) 또는 중간 풍화(moderately weathered) 이상으로 풍화가 진전된 암석이며, 국내 기준(KENCA, 2017)에서는 일축압축강도 30 MPa 이하인 연암 및 풍화암에 해당한다. 사면을 관통하진 않으나 비교적 긴 연장성을 가지는 불연속면 사이의 암반을 대상으로 계단 경로 파괴를 분석할 경우, 암교를 구성하는 암반(rock mass)의 전단 및 인장 강도는 Hoek-Brown 파괴기준을 따르는 암반 강도를 적용할 수 있으며, 이는 무결암(intact rock)의 강도에 비해 상대적으로 낮은 값을 가진다(Hoek and Brown, 1997).
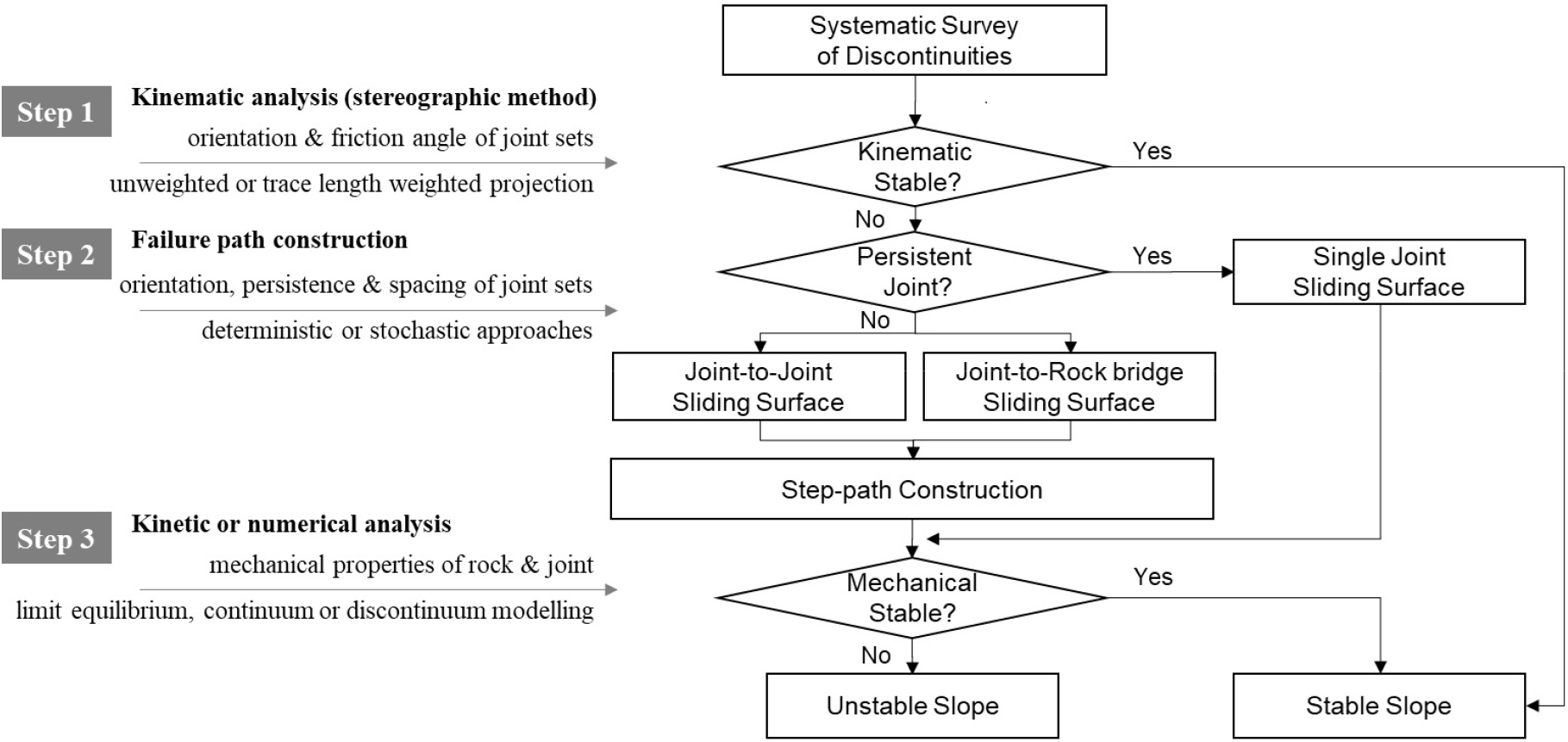
Fig. 8은 비연속성의 절리계가 발달하는 암반 사면에서 적용할 수 있는 안정성 평가 절차를 제시한 것이다. 계단 경로 파괴 평가를 위해서는 대상 사면의 체계적 절리 조사와 분석, 운동학적 해석과 함께 결정론적 또는 확률론적 계단 경로 파괴면에 대한 한계 평형 해석 또는 수치 해석 등의 안정성 평가를 수행하는 것이 필요하다. 안정성 평가 1단계에서 절리 길이를 가중치로 한 평사투영해석은 절리의 길이와 간격을 동시에 반영할 수 있어 운동학적 해석에서 계단 경로 파괴 가능성을 간접적으로 분석할 수 있다. 운동학적 평가에서 활동 파괴의 위험이 확인되고, 활동 유효면을 구성할 수 있는 절리가 비연속성이라면 2단계의 계단 파괴 경로 구성을 통해 3단계 안정성 평가를 수행할 필요가 있다. 3단계 평가에서 한계 평형 해석은 안전율 등 사면 안정성 평가의 중요한 기준을 설정할 수 있으므로 여전히 중요한 평가 방법이다. 또한 최근 절리 사이에서 인장 균열의 생성과 결합 등 암교의 파괴를 모사하는 불연속체 수치 해석(Huang et al., 2015; Zhang et al., 2020)의 증가는 계단 경로 파괴 해석의 향후 흐름을 보여주고 있어 주목할 필요가 있다. 이 경우, 계단 경로 파괴면 상의 절리-암교 활동면은 수치 해석의 결과로 제시된다.
평가 2단계의 파괴 경로 구성에서 대상 사면에서 수행된 체계적 선조사는 불연속면 분포 특성을 파악할 뿐 아니라 Fig. 6과 같이 절리 간격/길이가 충분히 낮은 구간을 분석할 수 있으므로 계단 경로 파괴의 가능성 분석과 함께 파괴 가능 위치를 특정하는 데 중요한 근거를 제공한다. 다만, 조사선과 교차하는 절리의 간격은 over-lap 상태의 절리 간격이므로 Fig. 7의 사례와 같이 측정된 절리 간격에 따라 on-lap 조건으로 절리의 길이를 재배열하는 것은 절리 밀집 구간이 일정한 폭을 가지는 대상으로 발달하고 있다는 전제가 필요하다. 또한 on-lap 조건의 절리 길이 재배열은 over-lap된 절리의 길이를 고려하지 않으므로 계단 경로 파괴면 구성에서 파괴의 위험을 증가시키는 영향을 줄 수 있으며, 이는 체계적 절리 조사를 통해서 절리 이격(gap)을 결정하는 것이 불가능하다는 현실적 한계를 반영하고 있다. 반면 조사선에서 측정한 절리 길이는 조사 가능한 암반에 노출된 절리의 길이이므로 절리면의 최대 직경을 고려하지 않는다 하더라도 실제 절리 길이보다 같거나 작기 때문에 측정된 절리 길이를 그대로 재배열하는 것은 계단 경로 파괴면 구성에서 파괴 위험을 감소시키는 영향을 줄 수 있다.
이와 같은 결정론적인 계단 경로 파괴면 구성 방법 이외에 Fig. 5의 불연속면 분포 특성에 대한 확률밀도함수를 통해 통계적 절리망을 생성시켜 파괴 경로를 구성하는 방법을 적용할 수 있다(Einstein, 1993; Kim et al., 2002; Jeong, 2007). 특히 실제 사면에서 직접적으로 불연속면을 조사하는 것이 불가능하거나, 사면 절취가 예정되어 있는 설계 단계의 경우에는 인근의 불연속면 분포 특성을 이용하여 확률론적 절리망을 생성하고, 이를 통하여 계단상 활동 파괴의 경로를 분석하거나 또는 불연속체 수치해석을 통하여 경단 경로 파괴를 분석하는 방법이 유용하다.