서 론
절리, 단층, 암맥, 층리면 등의 역학적 분리면은 지각 어디에서나 쉽게 관찰할 수 있다. 자연상의 절리는 복잡한 네트워크 구조를 형성하는 경우가 대부분이며 지하 암반의 역학적 및 수리지질학적 거동에 큰 영향을 미친다. 절리의 주요 영향에 대한 확고한 이해는 건설인프라, 지열 및 비전통 셰일가스 개발, 지하수 관리, 방사성폐기물 처분 등의 다양한 공학 프로젝트와 관련하여 도전적 과제로 인식되고 있다(Rutqvist and Stephansson, 2003; Tsang et al., 2005). 매우 복잡한 지층구조에서 유체 흐름의 채널 경로를 형성하는 자연 절리의 중요성은 절리성 암반에 대한 수치해석을 위한 현실성 있는 절리 네트워크(discrete fracture network, DFN) 모델에 대한 연구개발의 활성화를 이끌었다(Herbert, 1996).
절리성 암반에 대한 모델 수립에 있어서 가장 큰 어려움은 복잡한 삼차원 DFN 시스템에 대한 기하학적 표현이다. 자연상에서 절리는 다양한 규모의 파괴를 유발하는 특정 역학 조건으로 형성되는데, 이는 심부의 현지응력장에 영향을 받으며 교차절단, 분기, 종단, 휨, 간격 및 군집 등의 다양한 속성이 복잡하게 조합한 형태로 나타난다(Schultz, 2000). 이와 같은 지각 내부에 발달한 DFN의 삼차원 구조에 대한 직접적인 관찰은 거의 불가능하며 현장자료는 대부분 일차원 시추공 로깅 및 이차원 노두 맵핑 등의 극히 제한된 노출면으로부터 얻어진다. 따라서 절리성 암반의 기하학적 속성은 일차원 및 이차원에서 삼차원으로 또는 작은 표본으로부터 전체 해석영역을 추정하는 다양한 외삽법을 통하여 기재되었다.
투수율이 매우 낮은 결정질 암석이 분포하는 절리성 암반에서 DFN은 유체 흐름의 주요 통로로 작용하며(Berkowitz, 2002), 이때 유체 흐름은 절리 기하구조의 공간적 연결성과 개별절리의 투수량계수(transmissivity)에 크게 좌우된다. 그러나 현장에서 흔히 수행되는 대수층 양수시험 또는 패커시험 결과를 이용한 수리지질학적 연구는 지하수가 연속체 매질을 통해 흐른다는 가정에 기반한다(De Marsily, 1985; Hsieh et al., 1985). 양수시험 또는 패커시험은 시험정이 다공성 매질에 설치된 경우에 유용하지만 절리군이 체계적으로 발달한 절리성 암반 매질에 대한 적용에는 한계가 있다. 수리지질학 분야에서 빈번히 이용되는 다공성의 연속체 가정은 대표요소체적(representative elementary volume, REV) 내의 평균적 유체 흐름에 기반한 것인데(De Marsily, 1985), 다공성 매질의 REV 규모가 작더라도 절리성 암반에 대한 REV는 상대적으로 매우 클 수 있고 심지어는 존재하지 않을 수도 있다(Kulatilake and Panda, 2000). REV의 규모가 양수정과 관측정 사이의 거리보다 큰 경우 또는 REV를 설정할 수 없는 경우의 절리성 암반은 등가의 연속체 해석에 기반을 둔 연구방법의 적용이 어려우며, 절리성 암반에 대하여 등가의 연속체 해석을 수행하기 위해서는 암반의 수리적 거동에 관한 REV의 도출이 선행되어야 한다. 수리적 거동에 대한 REV는 암반의 수리전도텐서(hydraulic conductivity tensor)가 일정하게 유지되는 규모로 정의할 수 있으며 암반에 대한 등가의 연속체 해석은 REV 이상의 규모에 대하여 대칭의 2차 정부호 수리전도텐서를 적용할 수 있다.
현재까지 개발된 절리성 암반에 대한 유체유동모델은 연속체 유동모델, DFN 유동모델 및 등가의 연속체와 DFN을 결합한 하이브리드모델 등 크게 세 가지로 분류할 수 있다(Han and Um, 2015). 이들 중 DFN 유동모델은 절리성 암반에 대한 유체 흐름을 해석하는 데에 가장 많이 사용되는 모델이며, 특히 등가수리상수를 추정하기 어려운 지질 매질에 대한 유체유동 해석에 유용하다(Bear et al., 1993; Zimmerman and Bodvarsson, 1995). DFN 기반의 유체유동을 모사하기 위한 수치해석기법으로는 유한요소법, 경계요소법, 등가유로관모델(equivalent pipe model, EPM)이 제안된 바 있다(Han and Um, 2015). 저자는 등가유로관모델을 이용한 수치실험을 통하여 DFN 블록의 크기 및 절리의 기하학적 속성이 블록수리상수에 미치는 영향을 평가하고 절리의 방향, 빈도, 길이, 간극 등이 DFN 시스템의 REV와 수리적 이방성 및 등가연속체 특성에 미치는 영향을 보고하였다(Han and Um, 2015, 2016a, 2016b; Han et al., 2017). 본 연구는 등가유로관모델의 현장적용 제고를 목적으로 경상분지에 관입한 백악기 화강암이 분포하는 절리성 암반에 대하여 수리적 거동과 관련된 REV의 도출 가능성을 검토하였다. 또한, 본 연구는 REV 이상의 절리성 암반 규모에 대하여 등가의 연속체로 가정한 삼차원 수리전도텐서를 결정하는 작업흐름(workflow)을 제시하였다.
등가유로관모델
절리를 통과하는 비압축성의 유체 흐름은 식 (1)의 Navier-Stokes 방정식으로 설명할 수 있다(Zimmerman and Yeo, 2000).
여기서, ρ는 유체의 밀도, u는 속도 벡터, μ는 점성도, p는 수압이다. 식 (1)의 첫 번째 항은 비선형 유동과 관련된 관성력 항, 두 번째 항은 점성력 항, 세 번째 항은 압력구배(pressure head gradient)와 관련된 항이다(Kim and Yeo, 2019).
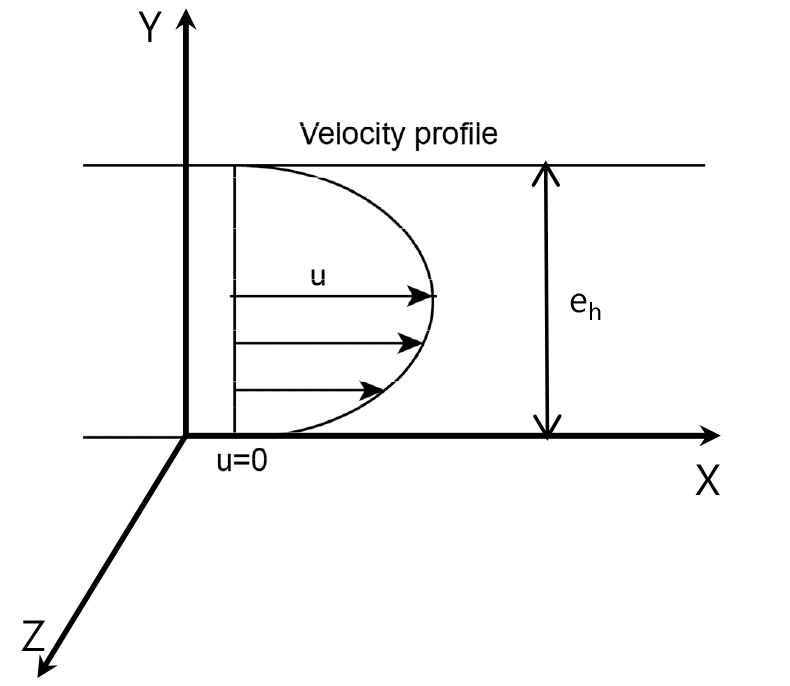
Fig. 1은 불투수성의 암석 매질에 발달한 평탄하고 평행한 절리 틈으로 가정된 등가유로관을 따라 흐르는 정상류 조건의 유체 흐름을 설명하는 모식도이다. 유체가 Y 및 Z 방향으로 흐름이 없고 X 방향으로 절리 수리간극(eh)의 상하부 경계면과 평행하게 흐른다면 식 (1)의 Navier-Stokes 방정식은 식 (2)와 같이 단순화할 수 있다.
식 (2)에 대하여 0에서 eh 구간까지 적분하고 경계조건으로 절리 수리간극의 상하부 경계인 y = 0 및 y = eh에서 u = 0을 적용하면 등가유로관에서 유속과 유량(Q)은 다음과 같이 유도할 수 있다.
식 (4)에서 b는 Z 방향으로 유로관의 폭, l은 유로관의 길이, p1 및 p2는 각각 유로관 입구 및 출구의 수압이다. 또한, 식 (4)에서 압력구배를 수두구배(△H)로 치환하여 등가유로관의 컨덕턴스 C(conductance)를 정의할 수 있으며, 여기서 g는 중력가속도, ν는 유체의 밀도와 관련된 동점성도이다.
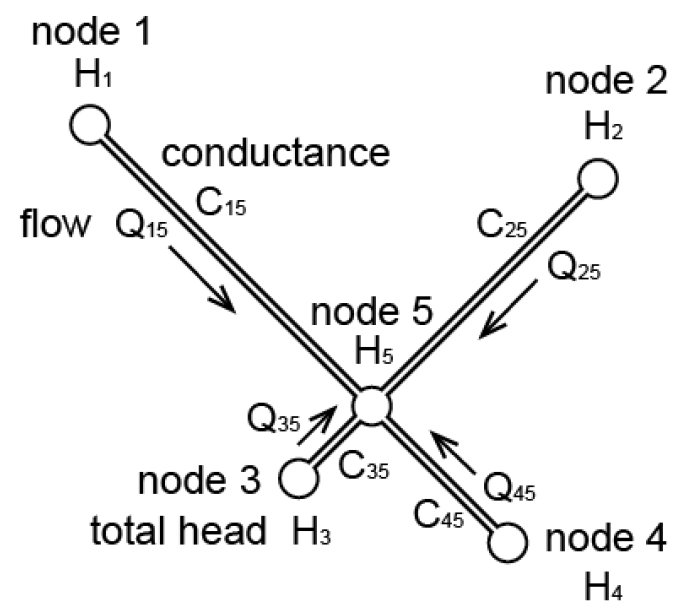
Fig. 2는 이차원 DFN에서 절리를 등가유로관으로 취급하였을 때 교차점인 노드(node)와 등가유로관의 연결구조를 나타낸 모식도이다. Hi는 ith 노드에서의 전수두이며 ith 노드와 jth 노드를 연결하는 등가유로관의 유량 및 컨덕턴스는 각각 Qij 및 Cij이다(Han and Um, 2016b). 등가유로관 주위의 암석매질이 불투수성 및 비압축성이며 유체가 등가유로관을 통해서만 흐른다고 가정하면 이차원 DFN의 jth 노드에서 유체의 순이득 및 순손실이 없으므로 ΣQij = ΣCij(Hi-Hj) = 0이며 jth 노드의 전수두 Hj는 다음과 같이 유도할 수 있다(Han and Um, 2016b).
연구지역의 DFN
연구지역은 부산광역시 기장군 일광면 원리 일대이며 이천리층을 관입한 백악기 흑운모 화강암으로 이루어진 절리성 암반이 분포한다. 연구지역 화강암의 주 구성 광물은 석영, 장석 및 흑운모 등이며, 4개의 NX 코어시료에서 측정된 공극률 및 흡수율의 평균값은 각각 0.50% 및 0.19%로 매우 낮게 평가되었다. 이는 연구지역의 암석매질이 치밀, 견고한 결정질 암석으로 이루어져 있음을 의미하며 암석매질을 통한 지하수의 흐름이 극히 제한적일 수 있음을 지시한다. 따라서 연구지역의 수리적 특성에 관한 연구는 등가유로관모델에 기반한 개별체 해석을 적용하는 것이 효과적일 수 있다.
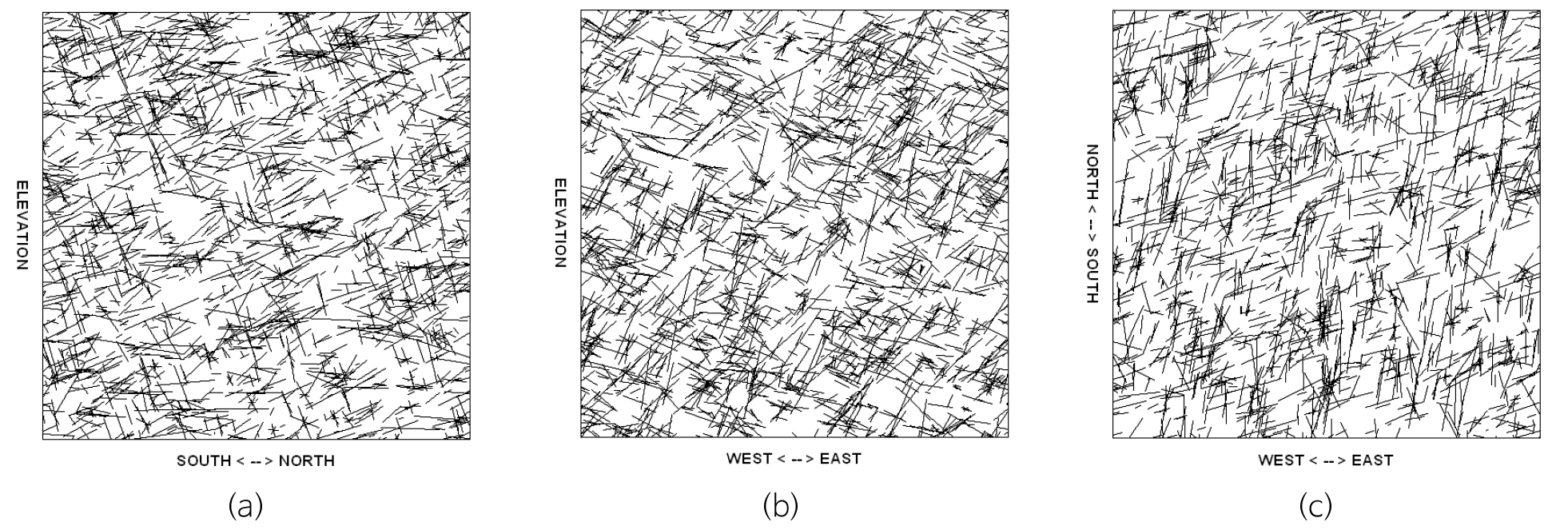
현장의 절리성 암반에 대한 DFN을 구현하기 위하여 암반 노출면에 대한 조사선 조사(scanline survey) 및 시추공 검층이 수행되었으며 조사 ‧ 기록된 절리 데이터를 분석하여 절리군이 구분되었다(Choi et al., 2010). Table 1은 연구지역의 절리성 암반에서 구분된 세 개의 절리군에 대하여 방향성, 빈도 및 연장성 분석을 수행하고 몬테칼로 모사기법을 이용하여 추계론적으로 생성된 삼차원 DFN으로부터 이차원 단면을 구성하였을 때 단면 방향에 따른 절리 트레이스의 기하학적 속성을 요약하였다. 이차원 영역에서 절리 트레이스의 면적빈도 및 길이분포는 절리의 방향성에 필연적으로 영향을 받는다. 예로서 주향이 N06E인 절리군 1의 절리는 남북수직단면보다 동서수직단면과 교차할 확률이 높으며 이에 따라 동서수직단면의 면적빈도(#/m2) 값이 남북수직단면보다 더욱 높다. 또한, 경사가 가장 완만한 절리군 3의 면적빈도 값은 두 수직단면보다 수평단면에서 가장 낮음을 알 수 있다. Fig. 3은 연구지역의 삼차원 DFN으로부터 15 m × 15 m 영역의 수직단면 및 수평면으로 이차원 DFN을 가시화한 결과이며 이를 위한 상세한 절차 및 방법론에 관한 사항은 선행연구(Choi et al., 2010; Noh and Um, 2012)를 참고할 수 있다.
Table 1.
Summary of fracture geometry parameters of the 2-D DFN
현장 규모의 DFN 시스템은 많은 개수의 절리를 포함하며, 등가유로관모델에서 절리 개수의 증가는 수치 연산과 관련된 시간을 가중하는 주요인이다. Wang et al.(2001)은 절리의 크기를 증가시키고 동시에 빈도를 줄이는 방법으로 현장 규모의 이차원 DFN 시스템을 보정하고 DFN 유동모델을 통한 지하수자원의 평가 사례를 보고한 바 있는데, 이때 DFN 시스템에 대한 보정은 필드에서 정성적으로 관찰한 절리의 간격 및 길이에 대한 경험적 판단에 근거하였다. 저자는 절리텐서(fracture tensor)의 성분 및 일차불변량이 이차원 DFN 시스템의 블록수리전도 특성에 미치는 영향을 분석하고, 절리의 빈도 및 길이의 함수인 절리텐서의 일차불변량이 절리의 빈도 및 길이를 보정하는 수단으로 활용할 수 있음을 보고한 바 있다(Um, 2019).
절리텐서는 절리의 방향성, 빈도, 길이분포 등의 기하학적 속성을 통합하여 정량화 할 수 있으며 절리를 원판형으로 가정할 때 k번째 절리군에 대한 삼차원 절리텐서(Fij(k))의 일반형은 식 (6)과 같다(Oda, 1982).
여기서, ρν는 단위체적당 절리개수(체적빈도), r은 절리의 길이, n은 절리면 수선 방향으로의 단위벡터, f(n,r)은 n과 r의 확률밀도함수, Ω/2는 단위반경의 반구표면에 대응하는 입체각, ni 및 nj (i, j = 1,2,3)는 각각 서로 직교하는 i 및 j 방향으로 벡터 n의 성분이다(Um, 2019). 이차원 절리텐서는 절리의 방향 및 길이분포가 서로 종속되지 않을 때 식 (6)으로부터 식 (7)과 같이 유도할 수 있다.
여기서, ρ는 절리의 면적빈도, θ는 절리 트레이스의 방향과 수평방향 사이의 각도, ni 및 nj (i, j = 1,2)는 각각 서로 직교하는 i 및 j 방향으로 벡터 n의 성분, f(r) 및 f(θ)는 각각 r 및 θ의 확률밀도함수이다(Um, 2019). 식 (7)의 절리텐서는 이차원 직교좌표계에서 행렬로 표현하면 식 (8)과 같다.
여기서, Fxx, Fxy, Fyx, Fyy는 절리텐서 F의 성분이다. F는 Fij와 Fji가 서로 같은 대칭행렬이므로 좌표변환을 통하여 서로 직교하는 두 방향으로 절리텐서의 주성분(principal components) F1 및 F2가 결정될 수 있으며 이로부터 절리텐서의 일차 불변량(first invariant, F0)은 식 (9)와 같이 유도할 수 있다(Kulatilake et al., 1994).
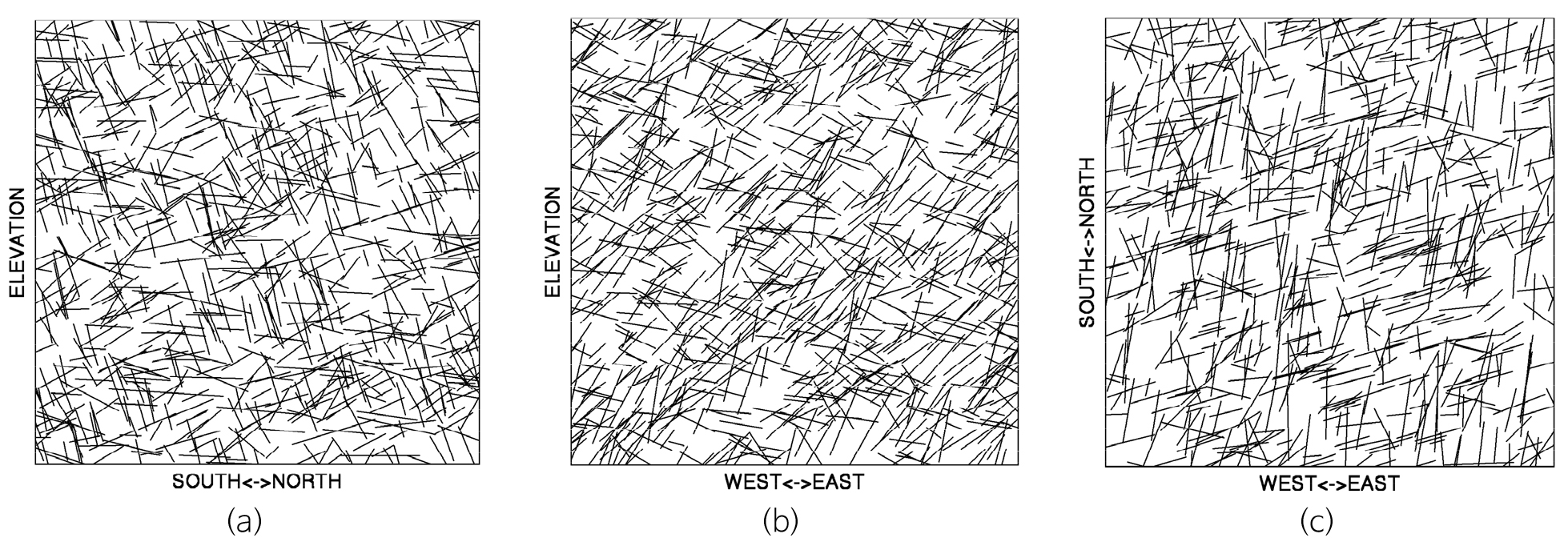
여기서, E(r2)은 절리군에서 절리 길이 제곱의 기댓값이다. 이차원 DFN 시스템의 F0는 절리의 빈도와 길이의 함수이며, 식 (9)의 F0와 절리의 빈도 및 길이 사이의 관계를 이용하여 F0를 상수로 고정하면 빈도의 변화에 따른 길이가 추정될 수 있다(Um, 2019). Um(2019)은 이차원 DFN에 대하여 절리텐서의 일차불변량을 이용한 보정 전후의 블록수리전도 특성이 서로 매우 유사함을 보고한 바 있다. Table 2는 Table 1에 수록된 절리의 빈도 및 길이를 바탕으로 산정한 F0 값과 이에 따라 보정된 DFN 시스템의 빈도 및 길이를 수록하였다. F0에 의해 보정된 이차원 DFN은 평균적으로 절리 트레이스의 면적빈도를 약 0.5배로 줄었을 때 길이가 약 1.8배 정도 증대되었다. Fig. 4는 연구지역의 이차원 DFN에 대하여 F0 값을 이용한 보정 후의 빈도 및 길이를 바탕으로 이차원 DFN을 구현한 결과인데, 보정 전의 Fig. 3과 비교하여 절리 트레이스 개수의 감소와 길이의 증가를 뚜렷이 인지할 수 있다. Fig. 4의 이차원 DFN에서 절리 트레이스의 연결구조는 선형의 등가유로관 연결망으로 취급할 수 있으며, 본 연구는 등가유로관모델을 이용하여 연구지역의 절리성 암반에 대한 블록수리전도 특성을 평가하였다.
Table 2.
Fracture geometry before and after correction using the first invariant of the 2-D fracture tensor
연구지역의 수리적 REV
본 연구는 연구지역의 이차원 DFN에 대한 수리적 REV의 크기를 결정하기 위하여 절리성 암반의 남북수직면, 동서수직면 및 수평면 등의 3개 단면에서 각각 최소 5 m × 5 m 크기의 정사각 해석영역을 설정하고 두 변을 각각 5 m씩 5단계로 증가시켜 최대 25 m × 25 m 크기까지 총 15개(3단면 × 5단계) 단면의 DFN을 고려하였다. 또한, 각각의 15개 단면에 대하여 매 30° 간격으로 12방향(Fig. 5)을 지정하여 총 180개의 DFN 블록이 구현되었다. 수치해석을 위한 경계조건은 해석영역의 좌우경계에 정수두(Φ1 > Φ2) 조건을 부여하였으며 상하경계는 Φ1에서 Φ2까지 선형으로 감소한다(Fig. 5). 한 변의 길이가 L인 정사각형의 해석영역에서 최대수두경사(I)는 I = (Φ1-Φ2)/L이며 최대수두경사의 방향(p)으로 단위시간 당 총 유량이 Qout일 때 p방향으로의 지향적(directional) 블록수리전도도(k(p))는 k(p) = Qout/IL이다. 이 연구에서는 SOR(successive over-relaxation)법을 적용하여 DFN 블록 내부의 모든 등가유로관 노드에서 전수두(식 (5))를 산정하고 이에 따른 DFN 블록의 Qout 및 k(p)를 계산하는 알고리듬(Han and Um, 2016b)을 사용하였다. 이때 노드의 전수두 산정에 필요한 유효수리간극 eh은 현장조사와 현장 수압시험(packer permeability test) 결과를 바탕으로 식 (10)을 이용하여 추정할 수 있다(Priest, 1993).
여기서, Qt는 현장수압시험을 통하여 평가하며, λ는 시추공 방향으로의 1-D 절리빈도(#/m), h는 수압시험 구간의 길이, H0는 주입압에 따른 압력수두이다.
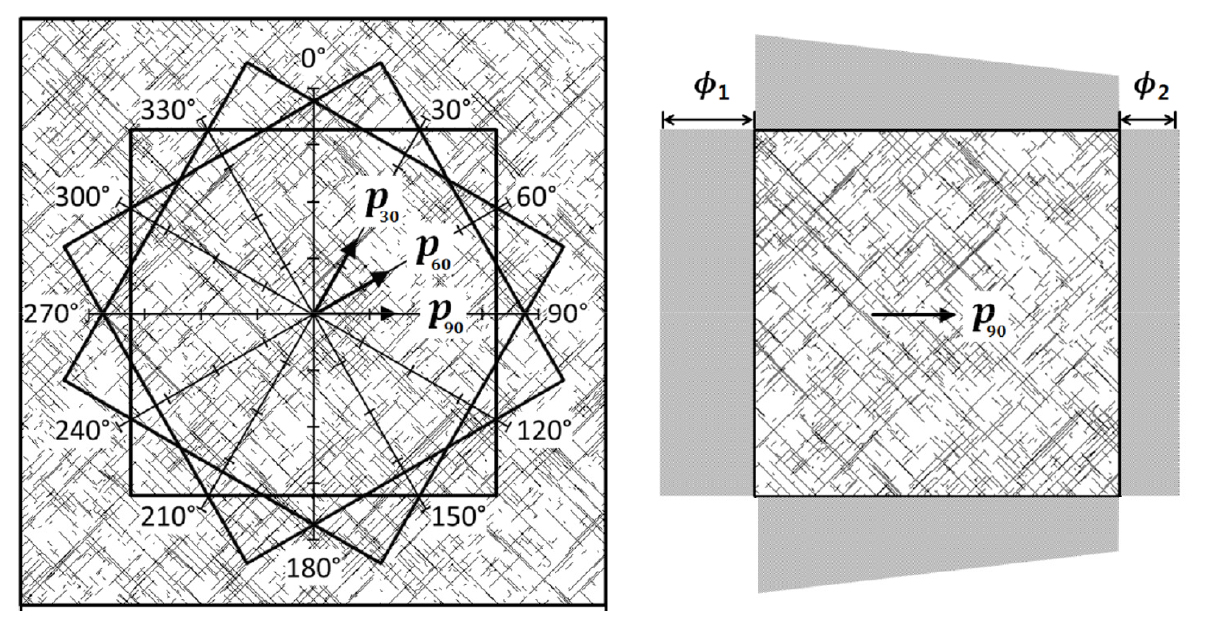
Fig. 5.
Construction of a 2-D square flow domain with two constant head boundaries (Φ1 > Φ2) by rotating the boundary and the hydraulic gradient at 30° intervals (Han and Um, 2016b).
본 연구는 현장에 설치된 4개소의 NX(Φ76) 수직 시추공을 대상으로 심도 5~11 m 구간에서 수행된 총 12회의 수압시험 결과를 이용하여 eh를 추정하였다. Table 3은 수압시험으로부터 평가된 현장 암반의 투수계수(K) 및 루전(Lugeon) 값을 요약하였다. 수압시험에 의한 현장의 투수계수는 최소 4.81E-07 m/s에서 최대 7.73E-06 m/s 범위로 나타났으며 평균 5.47E-06 m/s로 평가되었다. 이와 같은 현장수압시험 결과로부터 식 (10)을 이용하여 추정된 eh는 절리군 1, 2, 3에서 각각 0.30 mm, 0.14 mm, 0.10 mm이다. 연구지역에 분포하는 치밀한 결정질 화강암은 투수계수가 절리보다 상대적으로 매우 낮아 지하수 흐름이 없는 매질로 가정하였으며 절리는 절리군 마다 일정한 유효수리간극을 갖는 선형의 등가유로관으로 취급하였다.
Table 3.
Permeability and Lugeon values estimated from packer tests
Kantani(1984)와 Oda(1985)는 이차원 DFN 블록에서 다양한 방향으로 산정된 k(p)로부터 DFN 블록을 등가의 연속체로 가정한 이론적 블록수리전도도() 및 블록수리전도텐서()를 결정하는 식을 다음과 같이 유도하였다.
여기서, pi와 pj는 각각 수두경사에 평행한 단위벡터 p의 서로 수직인 i와 j 방향으로의 성분, δij는 크로네커 델타, N은 블록수리전도도 산정을 위해 고려한 방향의 총 개수이다(Han and Um, 2016b).
DFN 블록에 대한 등가의 연속체 취급 가능성은 와 k(p) 간의 상대오차(ER)를 도입하여 평가할 수 있으며, ER은 다음과 같다(Han and Um, 2015).
고려한 모든 방향에서 k(p) = 인 경우 식 (13)의 ER은 0이며, 이때 DFN 블록은 완전한 의미의 등가연속체로 취급될 수 있다(Han and Um, 2016b). 이차원 DFN 시스템의 최대 주 수리전도도 K11 및 최소 주 수리전도도 K22의 크기와 방향은 식 (12)의 로부터 결정할 수 있다. 또한, 평균 블록수리전도도 K0는 K11 및 K22의 평균으로 결정할 수 있으며 이와 같은 다양한 블록수리상수 추정에 대한 세부적인 내용은 저자의 선행연구를 참고할 수 있다(Han and Um, 2016a, 2016b).
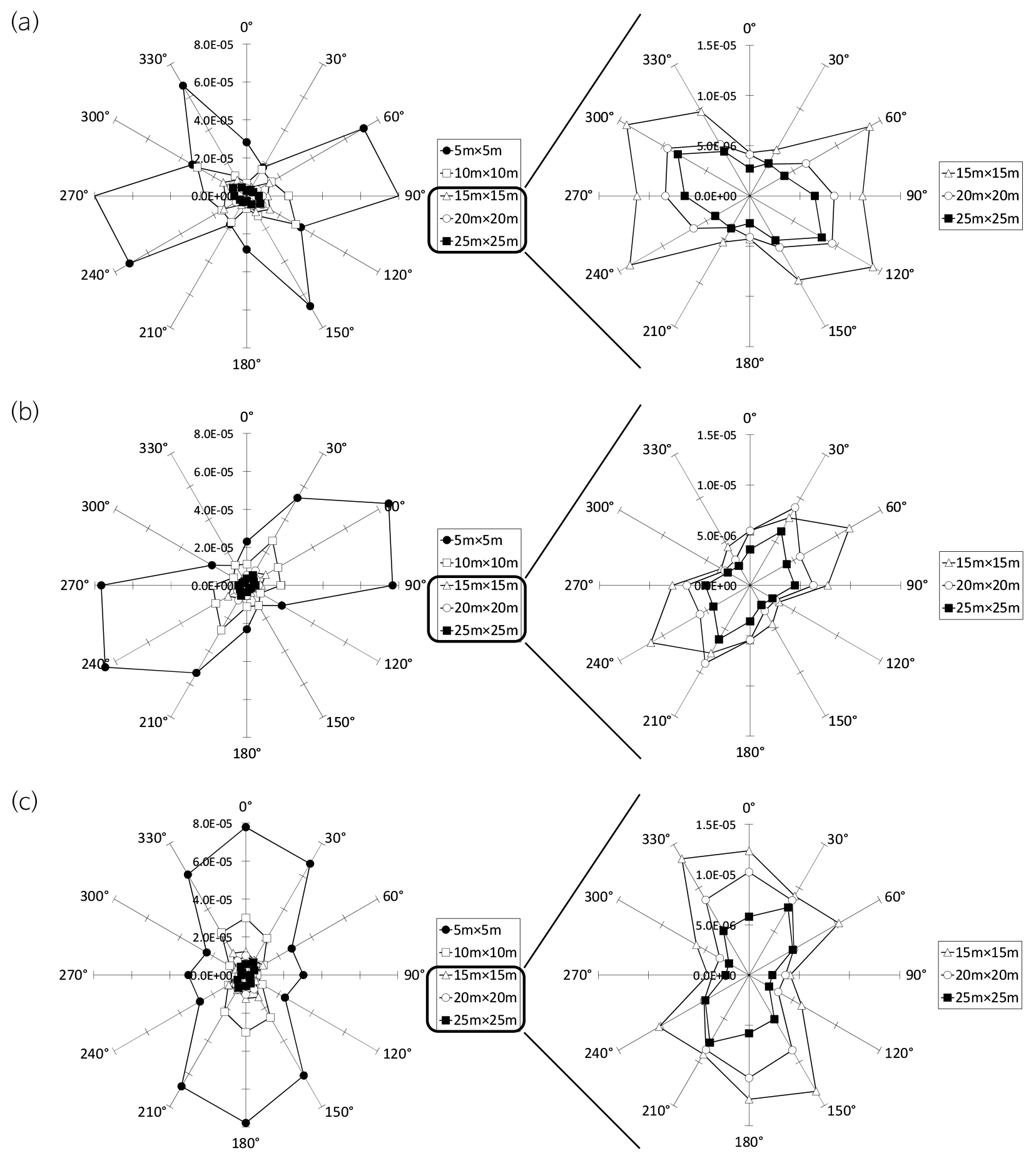
Fig. 6은 연구지역의 남북수직면, 동서수직면 및 수평면에서 이차원 DFN 블록(해석영역)의 크기를 5단계로 증가시키면서 각 크기 단계마다 매 30° 방향으로 총 12방향에 대하여 k(p)를 산정한 결과이다. Fig. 6a는 남북수직면의 DFN에 대한 방향에 따른 k(p)의 분포를 보여주는데, 5 m × 5 m의 수직 영역에서 k(p)는 수직 상향방향을 기준으로 30° ↔ 210° 방향으로 최소값을 나타내며 90° ↔ 270° 방향으로 최대값으로 증가하고 120° ↔ 300° 방향에서 다시 감소하다가 150° ↔ 300° 방향에서 또다시 증가하는 양상으로 방향에 따라 값이 매우 불규칙한 이방적 특성을 나타냈다. 이처럼 특정 방향으로 k(p)가 상대적으로 크게 산정되어 방향에 따른 값의 차이가 현저하게 발현된 이유는 DFN을 구성하는 절리의 길이분포에 비해 5 m × 5 m의 해석영역이 상대적으로 작은 데에 기인한다. 이는 해석영역의 규모가 작으면 해석영역의 폭과 유사한 길이의 절리가 존재할 가능성이 크고 이러한 절리의 방향성이 DFN의 블록수리전도 특성에 결정적인 영향을 미칠 수 있기 때문으로 판단된다.
남북수직면에서 지향적 k(p)의 변화는 DFN 블록의 크기를 10 m × 10 m로 확장하였을 때 5 m × 5 m 블록의 결과와 비교하여 다른 양상으로 도출되었다. 30° ↔ 210° 및 120° ↔ 300° 방향은 DFN 블록의 크기가 증대돼도 k(p) 값의 변화가 거의 없지만, 이외의 고려한 모든 방향은 k(p)가 감소하였음을 알 수 있다. 15 m × 15 m 이상의 블록 크기에서 산정한 k(p)는 상대적으로 매우 작은 값이 도출되어 같은 그래프에서 변화 양상을 파악하기 어려우므로 오른편에 확대하여 새로이 도시하였다. 15 m × 15 m 크기 이상의 DFN 블록에서 지향적 k(p)는 블록 크기가 증가함에 따라 뚜렷하게 감소하며 120° ↔ 300° 방향을 장축으로 하는 타원형의 이방성을 나타냈다. 또한, 블록 크기가 20 m × 20 m일 때와 25 m × 25 m인 경우를 비교하면 고려한 모든 방향에서 k(p)의 차이가 거의 없으며 서로 유사함을 인지할 수 있다. 이와 같은 결과는 연구지역의 남북수직단면에서 20 m × 20 m의 블록 크기가 이차원 DFN에 대한 수리적 REV로 적합할 수 있다는 직관을 제공한다.
Fig. 6b에 나타난 동서수직단면의 결과도 블록 크기를 5 m × 5 m에서 10 m × 10 m로 확장하였을 때 대부분의 방향에서 k(p)의 급격한 저하가 관찰되었으며, 블록 크기가 25 m × 25 m까지 단계별로 증가함에 따라 k(p)는 감소하여 타원형으로 수렴하는 것을 알 수 있다. 이와 같은 블록 크기에 따른 k(p)의 변화 양상은 Fig. 6c에 나타난 수평단면에서 얻은 결과에서도 유사하다. 특히, 수평면에서 구성된 등가유로관의 방향(Fig. 4c)은 절리의 주향 방향을 반영하며, 20 m × 20 m의 블록 크기에서 절리군 1의 주향방향(N06E)과 유사한 NS 방향(0° ↔ 180°)으로 유체 흐름이 가장 양호함을 확인할 수 있다. 이는 절리군 1의 유효수리간극이 가장 크고 절리 트레이스의 연속성이 타 절리군보다 양호한 데에 기인한 것으로 판단된다.
블록의 크기와 방향에 따른 k(p)의 변화 양상을 정량적으로 평가하기 위하여, 본 연구는 크기 단계별 DFN 블록에서 산정된 지향적 k(p)값으로부터 식 (11) 및 식 (12)를 통하여 및 를 산정하였다. 또한, 연구지역의 이차원 DFN 시스템에 대한 수리적 REV의 크기를 파악하고 이에 대한 등가연속체 취급 가능성을 평가하기 위하여 와 k(p) 간의 상대오차 ER(식 (13))이 산정되었는데, DFN에 대한 등가연속체 취급 기준은 ER = 0.2 이하로 설정하였다(Han and Um, 2016a, 2016b). Table 4는 블록 크기에 따라 산정된 ER 값과 이차원 수리전도텐서의 주성분 및 이들의 평균 블록수리전도도를 수록하였다.
Table 4.
Estimated ER values, 2-D principal hydraulic conductivities, and average block conductivities for DFN blocks of different sizes
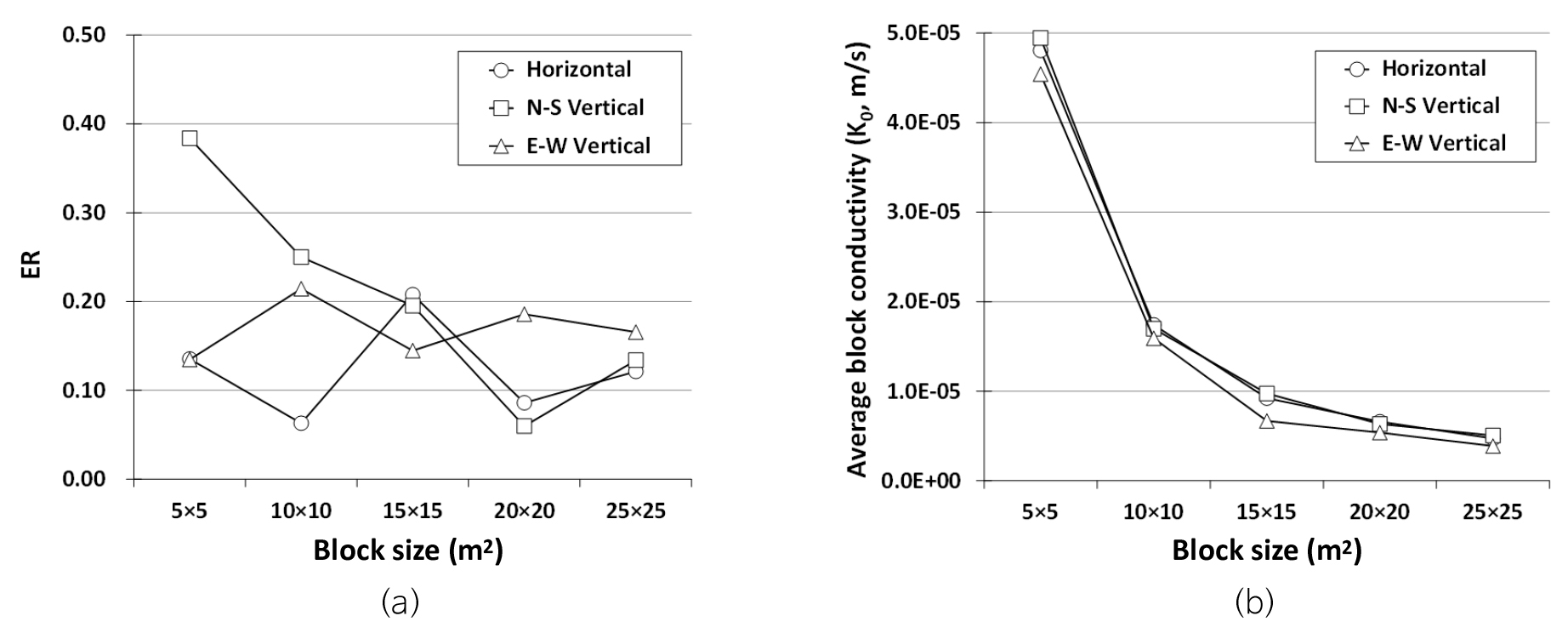
Fig. 7a는 블록 크기에 따라 산정된 ER의 변화를 보여주는데, 수평면, 남북수직면, 동서수직면 모두 20 m × 20 m 이상의 블록 크기에서 ER이 0.2 이하임을 알 수 있다. Fig. 7b에 도시한 평균 블록수리전도도는 수평면, 남북수직면, 동서수직면 모두 유사한 값을 나타내며 블록 크기의 증가에 따른 평균 블록수리전도도의 감쇠 패턴도 세 단면 간에 유의미한 차이를 인지하기 어렵다. 10 m × 10 m DFN 블록의 평균 블록수리전도도는 5 m × 5 m DFN 블록의 평균 블록수리전도도 대비 35% 내외로 대폭 감소하였으며, 이후 블록의 크기 증가에 따른 평균 블록수리전도도는 감소 폭이 점점 줄어들어 20 m × 20 m 이상에서 수렴하는 양상을 나타낸다. 이와 같은 블록 크기에 따른 ER 및 평균 블록수리전도도의 변화를 고려할 때 연구지역에 대한 수리적 REV 크기는 20 m × 20 m 정도로 평가할 수 있다. 또한, REV 이상의 DFN은 등가연속체로 취급할 수 있다.
삼차원 수리전도텐서
본 연구는 연구지역의 삼차원 수리전도텐서를 결정하기 위하여 삼차원 공간에서 수직 방향(elevation)을 회전축으로 하여 30° 간격으로 설정된 6개의 수직단면에 대한 이차원 DFN을 구현하였으며 각각의 DFN에 대하여 Fig. 5와 같이 30° 간격의 12방향으로 k(p)를 산정하였다. 이때 DFN 블록의 크기는 연구지역의 REV로 결정된 20 m × 20 m이다. 6개 수직단면의 주향은 각각, NS, N30E, N60E, EW, N60W, N30W이며, k(p)의 방향 수는 산술적으로 72(= 6 × 12)로 계산되지만, 각 수직단면의 상향인 0° 방향(plunge = -90°)과 하향인 180° 방향(plunge = 90°)은 6개 수직단면에서 중첩되므로 본 연구에서 고려한 방향의 수는 총 62개이다. 이처럼 설정된 62방향의 선주향(trend) 및 선경사(plunge)는 삼차원 공간에서 각각 30° 간격을 유지한다. Table 5는 총 62방향으로 산정된 k(p) 값을 요약하였다.
Table 5.
Estimated directional hydraulic conductivity, k(p) (m/s), in different flow directions for a 2-D DFN on six 20 m vertical square windows
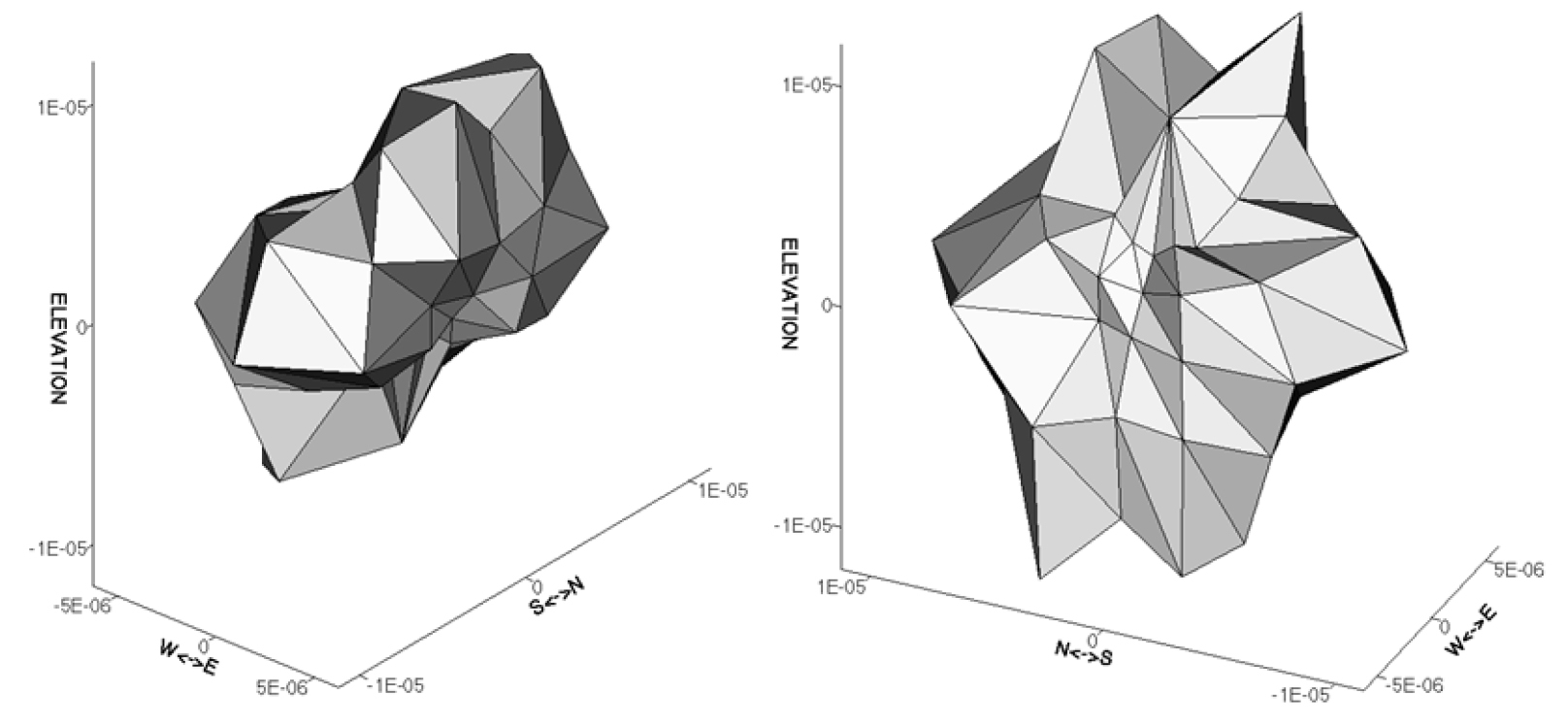
Fig. 8은 총 62방향으로 산정한 k(p)를 삼차원 공간에서 입체적으로 구성한 그림인데, 여기서 음(-) 부호의 k(p) 값은 방향이 반대임을 의미한다. 또한, Fig. 8은 삼차원상에서 k(p) 값의 변화 양상에 대한 이해를 돕기 위하여 NW 및 NE 향의 두 관점으로 구성하였다. 삼차원상에서 k(p)는 뚜렷한 이방성을 띠는 것을 확인할 수 있으며, 이는 연구지역에 발달한 절리의 기하학적 속성과 유효수리간극의 차이에 기인한 것으로 판단된다. 앞에서 REV 크기의 이차원 DFN에서 산정한 지향적 k(p)가 장축(K11)과 단축(K22)을 갖는 타원 형태임을 논의하였는데(Fig. 6), 삼차원상에서 62 방향으로 산정한 k(p)는 타원체로 형상화할 수 있다.
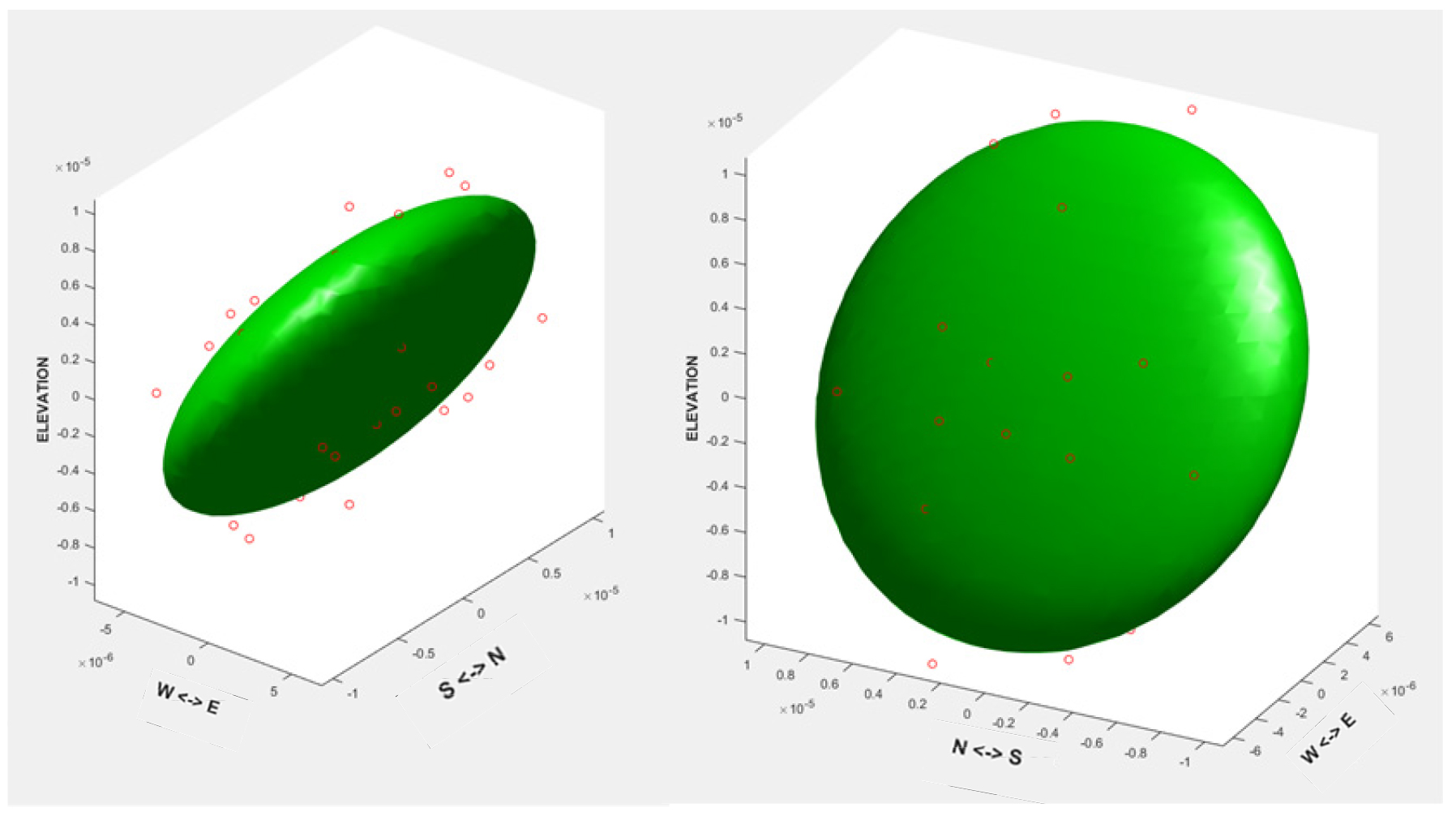
Fig. 9는 Table 5의 62개 k(p) 값을 사용하여 최적의 타원체를 구현한 결과이다. 타원체의 장축, 중간축, 단축의 크기는 삼차원 수리전도텐서의 주성분으로 취급할 수 있으며, 본 연구에서 추정한 삼차원 수리전도텐서의 크기와 방향이 Table 6에 요약되어 있다. 최대 주 수리전도도 K1과 중간 주 수리전도도 K2의 비(K1/K2)는 1.05로 서로 유사하며, K1과 최소 주 수리전도도 K3의 비(K1/K3)는 3.01이다. 이는 K1 및 K2가 K3의 3배 정도임을 의미하며 연구지역의 절리성 암반을 등가연속체로 가정한 삼차원 수리전도텐서가 K1, K2, K3를 주성분으로 하는 납작한 원반형의 타원체 형태임을 지시한다.
Table 6.
Estimated principal hydraulic conductivities and their orientations in 3-D space
| K1 = 1.1263E-05 m/s | K2 = 1.0713E-05 m/s | K3 = 3.7469E-06 m/s | |||
| Trend | Plunge | Trend | Plunge | Trend | Plunge |
| 324° | 45° | 204° | 26° | 96° | 33° |
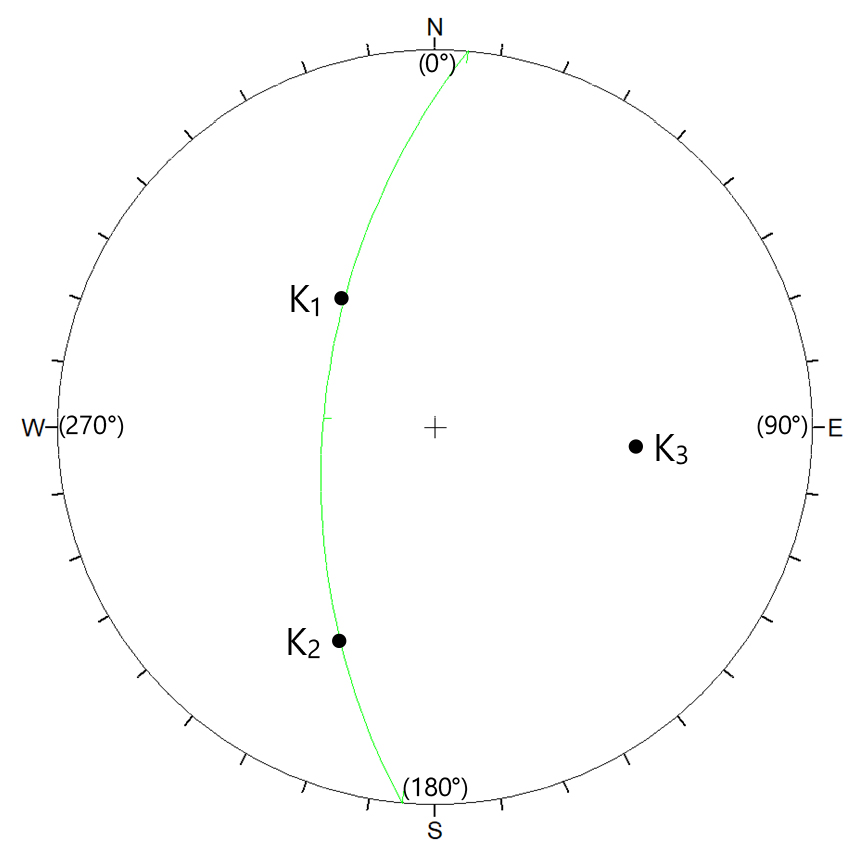
Fig. 10은 Table 6에 수록된 삼차원 수리전도텐서의 주성분(K1, K2, K3) 방향(선주향, 선경사)을 등각투영망에 작도한 결과인데, K1, K2, K3의 방향이 서로 직교하는 것을 알 수 있다. 투영망에 작도된 대원은 K1과 K2 방향벡터를 함께 포함하는 면에 해당하며 경사방향/경사가 275°/57°이다. K1과 K2를 포함하는 면의 방향성은 연구지역에서 구분된 세 절리군(Table 1) 중 절리군 1의 방향과 일치한다. 이와 같은 결과는 유효수리간극 eh가 가장 크고 절리의 연장성이 가장 양호한 절리군 1의 절리면을 따라 K1과 K2 방향이 형성됨을 지시하며, 이는 절리군 1로 구분된 절리가 연구지역의 결정질 화강암 암반에 대한 지하수 흐름에 주 통로로 작용한다고 평가할 수 있다.
결정질 화강암으로 이루어진 절리성 암반에 대하여 DFN 기반의 등가유로관모델을 활용하여 결정한 삼차원 수리전도텐서는 연구지역의 수리지질학적 연구를 위한 등가의 연속체 해석에 유용하게 활용할 수 있다. 치밀한 결정질의 절리성 암반에서 연속체 유동해석이 가능한 조건은 REV보다 큰 규모의 해석영역에서 ER이 0.2 이하인 경우이며, ER 값이 0.2 이하일 때 DFN 유동해석 결과가 등가의 연속체 유동해석 결과와 높은 상관성을 유지하는 것으로 평가된 바 있다(Lee and Um, 2017). 현장의 삼차원 수리전도텐서 추정을 위하여 이차원 DFN 단면에서 해석된 지향적 수리전도도를 바탕으로 삼차원으로 확장하는 본 연구의 워크플로우는 현재의 전산 하드웨어 성능과 수치연산에 소요되는 시간을 고려할 때 큰 장점이 있지만, 절리성 암반에 대한 지하수 유동해석에 있어서 이차원 해석이 갖는 근본적 한계도 간과할 수 없다. 절리성 암반의 역학적 등가물성과 관련하여 이차원 해석이 삼차원 해석보다 과대평가되는 이차원 모델의 한계가 보고된 바 있는데(Min and Thoraval, 2012), 수리적 등가물성에 대해서도 이차원 및 삼차원 해석의 비교를 통하여 이차원 모델의 한계를 정량적으로 고찰할 필요성이 제기된다. 또한, 본 연구는 절리를 선형의 등가유로관으로 취급하고 현장 수압시험 결과로부터 유효수리간극을 추정하는 방법을 적용하였는데, 절리의 거칠기에 따른 등가유로관의 굴곡도(tortuosity)가 수리상수에 미치는 영향도 논의되어야 한다.
결 론
본 연구는 부산 기장지역에 분포하는 백악기 흑운모 화강암 암반에 대하여 등가유로관모델을 통한 DFN 유체유동 해석을 수행하고 절리성 암반의 수리적 REV의 크기 및 삼차원 수리전도텐서를 추정하였다. 등가유로관모델은 수치연산 수행에 있어서 전산 하드웨어의 성능에 영향을 받으며 현장적용을 위한 해석영역의 확장에 따른 절리 개수 증가로 인하여 해석이 불가한 경우도 빈번하다. 연구지역의 DFN은 절리텐서의 일차불변량을 이용하여 절리의 빈도 및 길이가 보정되었다. 연구지역 분포하는 치밀한 결정질 화강암은 공극률 및 흡수율이 각각 0.50% 및 0.19%로 매우 낮게 측정되었으며 수리지질학적으로 지하수 흐름이 없는 불투수 매질로 가정할 수 있다. 연구지역에 분포하는 절리는 현장수압시험을 통하여 추정된 유효수리간극을 갖는 선형의 등가유로관으로 취급하였다. 연구지역의 수리적 거동을 대표하는 REV의 규모는 20 m × 20 m 영역으로 분석되었으며 REV 크기 이상의 DFN은 등가의 연속체 해석이 가능한 것으로 평가되었다. 연구지역의 DFN으로부터 추정된 지향적 블록수리전도도와 삼차원 수리전도텐서는 현장의 수리적 거동과 관련하여 이방성을 지시하며, 이는 절리군의 개수, 방향, 빈도, 크기 등의 기하학적 속성과 유효수리간극의 차이에 기인한 것으로 판단된다. 연구지역의 삼차원 수리전도텐서는 최대 주 수리전도도 K1과 중간 주 수리전도도 K2의 비(K1/K2)가 1.05이며 K1과 최소 주 수리전도도 K3의 비(K1/K3)가 3.01인 원반형의 타원체로 결정되었다. 연구지역에서 K1과 K2 방향벡터를 함께 포함하는 면의 방향성은 유효수리간극이 가장 크고 연장성이 가장 양호한 절리군의 방향과 일치한다. 현장 규모의 삼차원 수리전도텐서를 결정하기 위한 본 연구의 워크플로우는 수리지질학적 연구를 위한 등가의 연속체 해석에 유용하게 활용할 수 있다. 본 연구는 절리를 거칠기가 없는 선형의 등가유로관으로 가정하고 이차원 해석을 통하여 삼차원 수리전도텐서 추정하였는데, 이에 따른 한계에 관한 후속연구가 필요하며 심도 있는 논의 및 고찰이 기대된다.