서 론

결정질 석회암을 구성하는 방해석 내에는 쌍정이 흔하게 관찰되는데, 쌍정은 방해석이 생성된 후 역학적 변형의 결과로써 약 10 MPa의 낮은 차응력 하에서 e[011¯2]면을 따라 발생한다. 이동의 방향은 e면과 결정면 기호가 r인 r[1011] 면이 만나서 이루는 선을 따라서 발생한다(Fig. 1). 이때 발생하는 변형률은 부피의 변화가 없는 단순 전단변형으로 취급된다. 단순 전단변형은 크기가 같은 압축응력과 인장응력이 직각으로 작용할 때 압축응력 및 인장응력 축과 45°의 각도를 이루게 된다. 또한 방해석 입자에 작용한 응력과 e면의 수직선, 이동의 방향 및 방해석의 결정의 c-축은 한 평면에 존재하게 되며 각각의 관계는 Fig. 2와 같다.

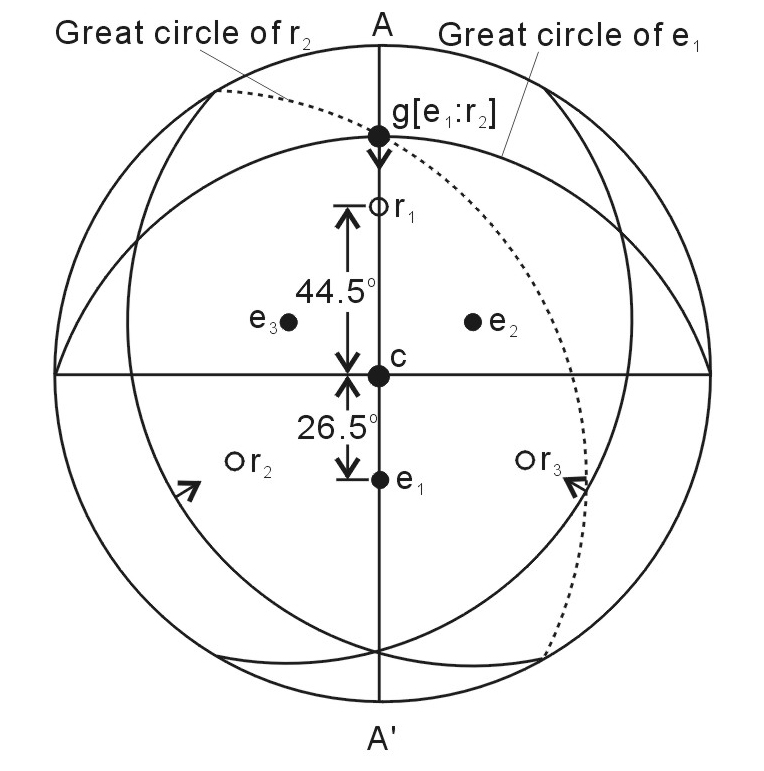
Fig. 1.

Crystallography geometry of calcite twin plotted on the lower hemisphere stereographic projection (Groshong, 1974). c is the optic axis of calcite and e₁, e₂ and e₃ are poles of e[0112] plane and r₁, r₂ and r₃ are poles of the r[1011] plane. Twin glide occurs parallel to g, the line of intersection of the e and r plane.

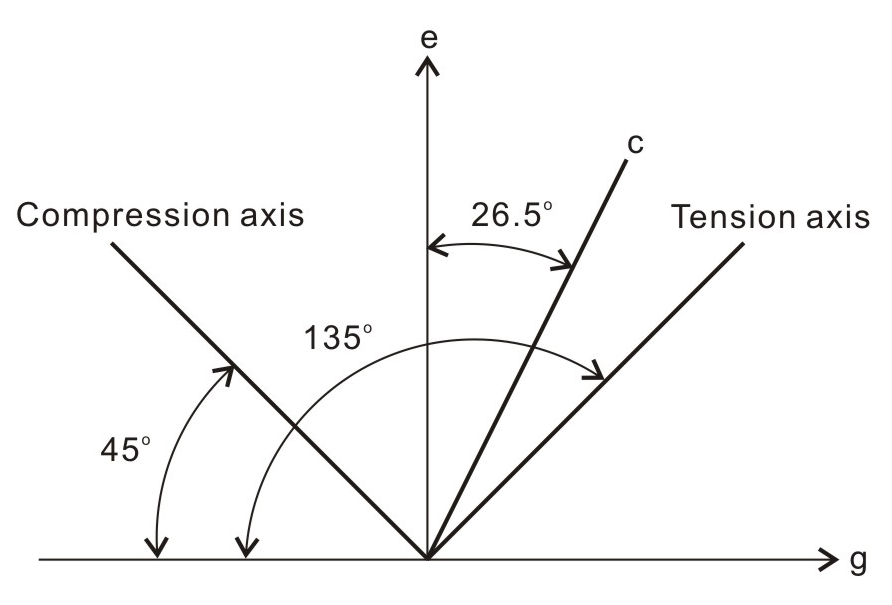
Fig. 2.

Directions of comression and tension axies on e-g plane of the cross-section A-A’ in Fig. 1. The angle between the c-axis and the pole to e-lamellae is 26.5°.

Turner(1953)는 위의 관계를 이용하여 각각의 쌍정면에서 압축응력 및 인장응력의 방향을 계산한 후, 압축응력 및 인장응력의 방향을 평사투영하여 최적의 응력 방향을 계산하는 Tunner Dynamic Analysis(TDA)를 개발하였고, 많은 연구자에 의하여 고응력장 연구에 TDA법이 이용되었다(Friedman and Conger, 1964; Friedman and Stearns, 1972; Rowe and Rutter, 1990). TDA가 개발된 이후 더욱 발전된 고응력장 및 변형율 측정법들이 개발되었는데, Spang(1972)은 텐서를 이용한 Numerical Dynamic Analysis에 의한 주응력의 상대적인 크기와 방향을 결정하는 방법을 개발하였으며, Groshong(1972)은 쌍정의 두께 및 개수를 이용하여 쌍정이 생성되면서 발생한 전단 변형율의 주변형율 크기와 방향은 Strain Gage Technique를 이용하여 계산하였다. 또한 쌍정이 생성된 방해석 입자와 쌍정이 생성되지 않은 입자의 방향을 측정하여 응력장의 절대적인 크기를 측정하려는 연구도 활발하게 진행되었다(Jamison and Spang, 1976; Laurent et al., 1981, 1990; Lacombe and Laurent, 1992). 쌍정은 동일한 전단응력하에서도 생성온도에 따라 형태가 달라지거나 두께의 차이가 발생한다. 실내실험에 의한 연구 결과 낮은 온도에서 생성된 방해석 쌍정은 여러 개의 얇은 쌍정이 생성되는 반면, 높은 온도에서 생성되는 쌍정은 소수의 두꺼운 쌍정이 생성된다(Heard, 1963; Groshong, 1974). Ferrill(1991)은 프랑스 동부의 Subalpine Chain 석회암층에서 탄화 반사도(vitrinite reflectance)와 일라이트 결정도(illite crystallinity)를 이용하여 측정된 속성온도와 쌍정의 변형률, 평균 두께 및 평균 치밀도를 비교하여 쌍정이 생성될 당시의 온도를 추정하였다.

본 연구는 태백일원에 분포하는 조선누층군 두위봉형의 풍촌석회암 내에 발달해 있는 방해석 쌍정을 측정하여 석회암의 속성환경 온도와 이 지역에 변형을 일으킨 고응력장을 규명하고자 한다. 방해석 입자의 c-축과 쌍정 e[0112] 면을 분석하여 고응력장의 방향성을 규명하였으며, 쌍정의 평균 변형율, 두께 및 치밀도 등을 계산하여 쌍정의 생성온도를 추정하였다. 본 연구에서 쌍정을 이용하여 규명된 고응력장은 기 연구된 고응력장의 방향성과 비교하여 연구지역에서의 방해석 쌍정을 생성시킨 고응력장의 상대적 시기를 규명하였다.

응력장 계산

방해석에 서로 직각인 압축응력과 인장응력이 작용할 때 발생하는 단순 전단변형률을 모아원으로 나타내면 Fig. 3과 같다. 이때의 전단변형률을 압축응력과 인장응력의 기준좌표축에 나타내면 식 (1)의 제2차 텐서의 형태로 나타낼 수 있다.

식 (1)은 좌표축이 압축응력과 인장응력인 경우에 표시한 전단변형률이므로 박편에서 쌍정의 측정에 이용된 좌표축으로 전단변형률을 나타내기 위해서는 좌표축을 회전시켜야 한다. 식 (1)은 제2차 텐서이므로 텐서 회전을 이용하여 박편의 좌표축에서 계산된 전단변형률은 식 (2)로 표시할 수 있다.

여기서, p, q, r은 압축응력의 좌표계에 대한 방향코사인이고, p', q', r'은 인장응력의 좌표계에 대한 방향코사인이다. 식 (2)는 쌍정 하나의 입자에서 측정한 전단변형률인데, 일반적으로 하나의 시료에서 50개 이상의 방해석 입자를 측정하게 되므로 식 (2)와 같은 행렬이 50개 이상 만들어지게 되어 50개 이상의 압축응력 및 인장응력의 방향이 나오게 된다. 그러나 시료에 작용한 응력은 한 방향이므로 식 (2)에서 계산된 응력장의 최적값을 찾아야 한다. Spang(1972)은 각각의 입자에서 계산된 식 (2)의 모든 행렬을 합한 후 쌍정 세트의 수로 나누어 전체 응력 텐서(bulk stress tensor)를 만들었다. 이러한 전체 응력 텐서는 주응력의 상대적 크기와 방향을 나타내는 타원이 되며, 주응력의 상대적 크기와 방향은 고유 값(eigenvalue)과 고유 벡터(eigenvector)를 이용하여 구할 수 있다.

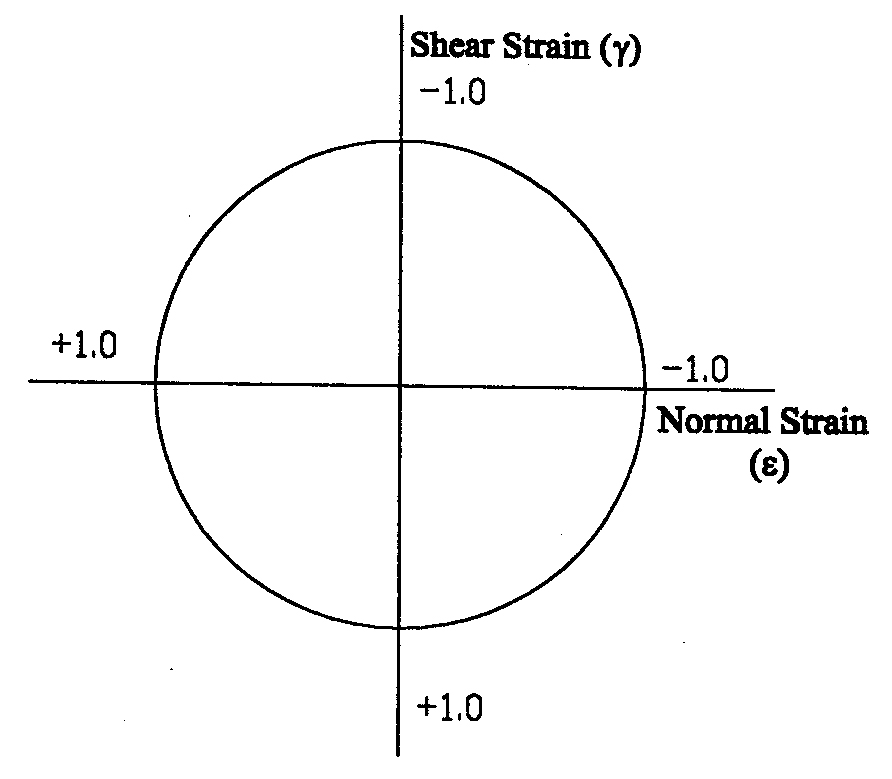
Fig. 3.

Mohr circle of infinitesimal strain for calcite twin lamellae (Spang, 1972); compression = positive, extension = negative, right-hand shear = positive, left-hand shear = negative.

변형률 계산

방해석 쌍정에 발생한 변형률 계산은 주로 Groshong(1972)에 의하여 이루어졌으며, 본 연구에서 사용된 변형률 계산 프로그램인 CSG(Calcite Strain Gage)의 이론적 바탕이다. 만약 직각인 방해석이 응력을 받아 Fig. 4와 같이 변형되었다면 쌍정이 생성되면서 발생한 전단변형률은 식 (3)과 같이 나타낼 수 있다.

여기서, t는 방해석 입자의 폭이고, t_i는 쌍정의 두께이며, α는 쌍정과 원래 광물이 이루는 각으로 Handin and Griggs(1951)에 의하면 38.17°이다. 이때 하나의 쌍정 세트에서 측정된 전단변형률, Γ_eg를 박편에서 쌍정의 측정에 이용된 좌표축상에 표시하면 식 (4)와 같다.

여기서, (l_e, m_e, n_e)과 (l_g, m_g, n_g)는 각각 e-와 g-축의 방향코사인이다(Fig. 4). 위의 식 (4)에서 구하고자 하는 값은 변형률 εx,εy,Γxy,Γyz,Γzx로 5개의 쌍정을 측정하면 정확한 해를 구할 수 있다. 그러나 방해석 쌍정 측정에서는 하나의 시료에서 50개 이상을 측정하므로 유일해가 존재하지 않는 방정식(overestimated equation)이 된다. 따라서 쌍정이 생성되면서 발생한 변형률의 최적값은 최소자승법(least square method)를 이용하여 구할 수 있다. 각각의 쌍정 세트에서 측정된 변형률은 식 (5)의 형태로 나타낼 수 있다.

여기서, Γ_i는 쌍정 세트 i에서 측정된 전단변형률이고, β1=εx,β2=εy,β3=Γxy,β4=Γyz,β5=Γzx이며, x_ij (j = 1~5)는 쌍정 세트 i에서 측정된 방향코사인의 값들이다(식 (4) 참조).

하나의 시료에 대하여 50개의 쌍정을 측정하게 되면, 식 (5)를 50개 얻게 되어 50 × 5 크기의 행렬이 되며, 최소자승법을 이용하여 구한 쌍정의 변형률은 식 (6)으로 나타낼 수 있다.

여기서, X는 식 (5)의 x_ij로 이루어진 행렬이고, Y는 측정된 변형률로써 Γ_i로 이루어진 행 행렬(column matrix)이며, X'는 행렬 X의 전치행렬(transpose), 윗첨자 -1은 역행렬(inverse)을 나타낸다. 식 (6)을 전개하면 쌍정에 의한 변형률이 구해지고, 주변형률의 크기 및 방향은 식 (7)의 행렬에서 고유 값 및 고유 벡터를 이용하여 구할 수 있다.

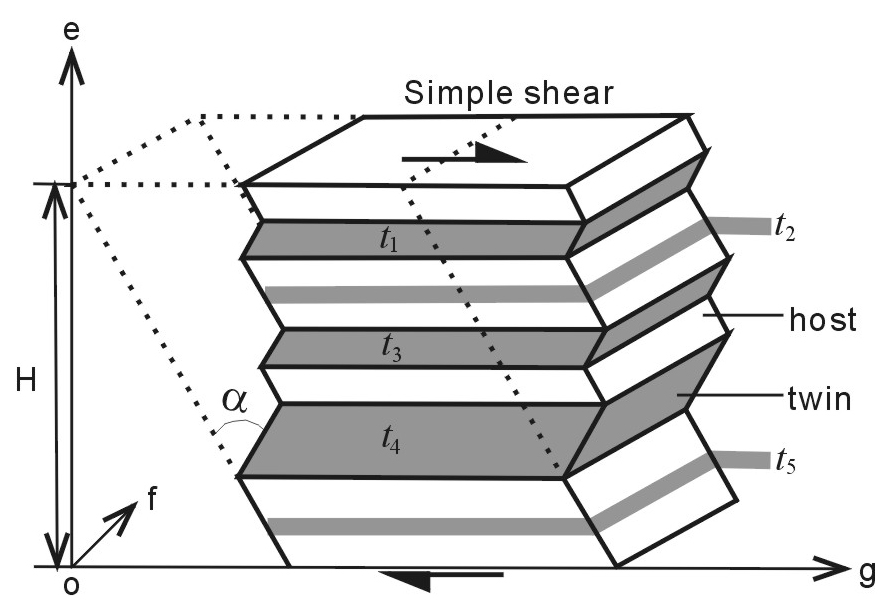
Fig. 4.

Geometry of twins in a calcite grain produced by simple shear strain. The f axis is perpendicular to the ge plane. Dashed lines indicate the outline of the original untwinned calcite grain. Shaded and unshaded areas show the twinned laellae and host portion (untwinned lamellae) of the grain. α is the angle of rotation of the grain edge from the host portion to the twinned lamellae.

연구지역 지질

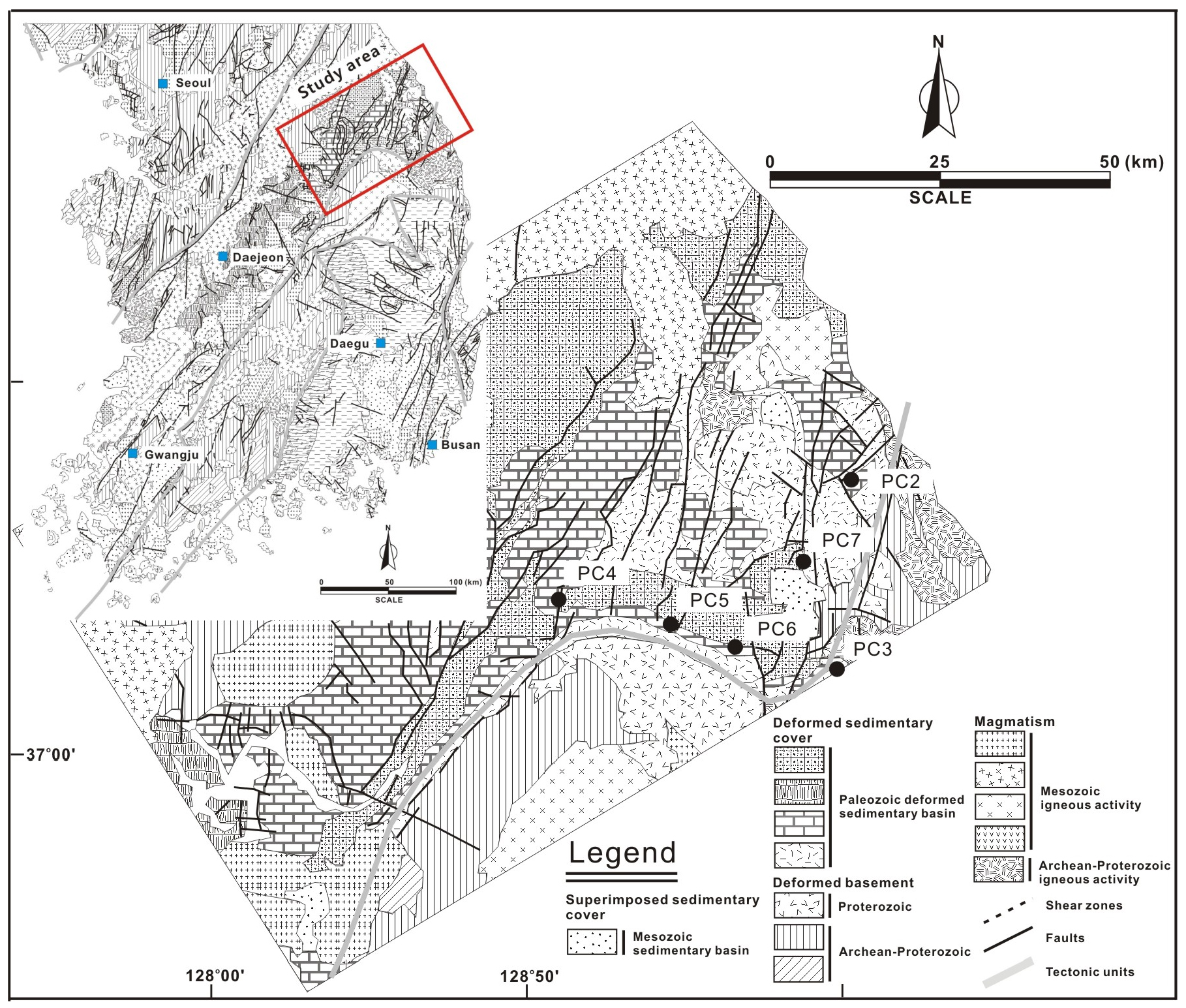
하부고생대에 분포하는 석회암층을 포함하고 있는 조선누층군의 다섯 형태 중 하나인 두위봉형은 옥천습곡대의 동북부 지역에 속하는 강원도 태백 일대에 넓게 분포하고 있다. 두위봉형을 이루고있는 아홉 개의 층 중 풍촌층은 하부에 주로 암회색 또는 암녹색의 슬레이트와 천매암으로 구성되어 있으며, 사질암과 석회암이 협재되어 있는 묘봉층과 층의 상부에 주로 암회색의 셰일과 협재 된 사암층으로 구성되어 있다. 암상은 주로 석회질 성분과 규질 성분이 층리면에 평행하게 발달해 있는 화절층 사이에 정합으로 놓여있다. 석회암으로 이루어진 풍촌층은 주로 유백색, 암회색 및 담홍색 등의 결정질 석회암으로 구성되어 있으며, 역질층 간 석회암과 돌로마이트질 석회암도 협재되어 있다. 층 하부와 중부에는 얇은 암회색 셰일이 수반되는데, 이 층의 석회암은 층리의 발달이 불량한 비교적 순수한 양질의 결정질 석회암으로 구성되어 있다(Fig. 5). 동점지역의 최하부에서는 우이드(ooid)와 로도이드(rhodoid)를 주성분으로 하는 입자암(grainstone)이 우세하고, 중상부에는 변질을 많이 받은 결정질 석회암으로 이루어져 있다. 풍촌층의 퇴적학적 연구를 살펴보면 대부분의 퇴적구조가 사라진 결정질 석회암이 우세하게 나타난다. 하지만 풍촌층 내에서 발견되는 우이드, 로도이드 및 극피류 화석들은 풍촌층이 수심 10 m 이내의 얕은 환경에서 퇴적되었음을 지시한다(Lee et al., 1992). 층의 두께는 약 150~300 m 정도이다.

Fig. 5.

Geological map of the study area and sampling locations.

연구방법

태백지역의 백운산 향사대를 중심으로 풍촌층의 노두로 부터 13개의 시료를 채취하였으나 단지 6개의 시료에서만 쌍정이 관찰되었다. 시료채취는 연구지역을 대표할 수 있도록 시료채취 지역을 가능한 한 골고루 분산시켰으며, 시료를 노두에서 채취하기 전에 편평하고 평행하지 않은 두 면의 주향과 경사를 측정하여 시료의 방향을 노두에서와 같이 유지하는 정향시료법(oriented sampling)을 이용하였다. 또한 시료채취 시 층리면의 주향과 경사를 측정하여 층리면의 수정에 이용하였다. 각각의 시료에서 수평 및 수직방향 2개의 박편을 제작하였다. 박편의 두께는 쌍정을 용이하게 측정하기 위하여 일반박편의 1/3~1/4 두께인 7~10 µm으로 하였으며, 다이아몬드 연마제를 이용하여 박편의 표면을 깨끗하게 연마하였다. 쌍정의 측정은 일본 Nikon사 제품의 4축 유니버셜 스테이지를 이용하였으며, 수평 및 수직의 박편에서 25개씩의 입자를 선정하여 총 50개의 입자에 발달한 쌍정을 측정하였다(Groshong, 1974). 방해석 쌍정을 이용한 고응력장 방향 및 변형률 분석은 Georgia Southern University의 M.A. Evans에 의하여 개발된 Calcite Strain Gauge(CSG) Technique프로그램을 이용하였다(Evans and Groshong, 1994). CSG 프로그램을 이용한 쌍정의 분석은 측정된 자료의 입력, 결과 출력 및 자료의 보정으로 나뉜다. CSG 프로그램에 입력되는 측정변수는 각각의 방해석 입자에서 측정된 c-축의 방향 및 경사, 쌍정면의 주향 및 경사, 한 입자에 생성된 쌍정의 개수 및 평균 두께, 방해석 입자의 크기이며, 쌍정의 개수 및 두께는 두께가 1 µm 이상의 두꺼운 쌍정과 1 µm 이하의 얇은 쌍정을 구별하여 입력한다. 또한 쌍정은 수평과 수직으로 제작된 서로 직각인 두 개의 박편에서 서로 다른 기준의 좌표축 상에서 측정되었다. 그러므로 수직의 박편에서 측정된 자료와 수평의 박편에서 측정된 자료를 종합하기 위해서는 수직의 좌표축에서 측정된 자료에 대하여 방향 및 경사 수정이 필요하고, 이러한 방향의 수정은 수직의 박편에 적용된 좌표축의 방향코사인을 이용하여 실시한다.

이상의 입력자료에 의하여 계산되어 출력되는 결과는 크게 4부분으로 구성되어 있다. 첫 번째 부분은 자료입력의 정확성을 확인하기 위하여 입력된 자료를 출력하는 부분이며, 두 번째 부분은 각 입자의 c-축의 방향, 쌍정면의 수직선의 방향, c-축과 쌍정면의 수직선이 이루는 각도, 각각의 쌍정에서 계산된 압축응력의 방향 및 인장응력의 방향으로 구성되어 있다. c-축과 쌍정면의 수직선이 이루는 각도는 쌍정과 c-축 측정의 정확성을 지시하여, 만약 이 각도가 26.5° ± 3°를 이루지 못하면 이 입자에서 측정된 자료는 다시 측정하거나 폐기되어야 한다. 세 번째 부분은 각각의 입자에서 측정된 응력장의 방향에서 Spang(1972)의 수치해석에 의한 주응력의 상대적 크기 및 방향과 Groshong(1974)의 최소자승법(least square analysis)에 의한 주변형률의 크기 및 방향, 쌍정의 변형률(twin strain), 쌍정의 평균 치밀도(mean twin intensity) 및 쌍정의 평균 두께(mean twin width)에 대한 결과로 이루어져 있다. 쌍정의 변형률, 평균 치밀도 및 평균 두께는 쌍정이 생성될 때의 온도를 추정하는 자료로 이용된다(Ferrill, 1991). 네 번째 부분은 세 번째 부분에서 계산된 응력장과 생성된 쌍정의 적합성 여부를 검증하는 부분으로, 양의 기대값을(Positive Expected Value, PEV) 가지는 쌍정은 계산된 응력장과 일치하는 쌍정이나, 음의 기대값을(Negative Expected Value, NEV) 보이는 쌍정은 계산된 응력장 하에서는 생성되지 않았을 쌍정임을 지시한다. 일반적으로 측정 오차 등으로 인하여 약간의 입자에서 NEV는 나타나지만, 만약 하나의 시료에서 NEV를 보이는 쌍정이 40%에 가까운 값을 나타내면 2번 이상의 응력장이 작용하였음을 지시한다(Groshong, 1972; Teufel, 1990). 이런 경우에는 PEV를 보이는 쌍정과 NEV를 나타내는 쌍정을 분리하여 다시 계산하면 2번 이상 작용한 응력장을 구별할 수 있다. 일반적으로 NEV를 나타내는 쌍정의 숫자가 10~30% 정도인 경우, 전체 쌍정에서 가장 큰 편차를 보이는 20%의 쌍정을 제거하면 결과가 향상되고(Groshong, 1974; Groshong et al., 1984) CSG 프로그램에서는 자동적으로 이러한 기능을 수행한다.

연구결과

4축 유니버셜 스테이지가 장착된 편광현미경을 이용하여 각 시료에서 나타나는 방해석 쌍정의 분포상태, 입자들의 크기, 쌍정의 두께, 그리고 쌍정의 개수 등을 관찰 및 측정하였다. 4개의 시료(PC2, PC3, PC4, PC5)에서는 시료 전체에 쌍정이 골고루 분포하는 반면, 2개의 시료(PC6, PC7)에서는 주로 방해석 맥에서만 쌍정이 관찰되었다. 쌍정의 형태로는 좁은 직선형의 쌍정, 넓은 직선형의 쌍정, 넓은 곡선형의 쌍정과 넓은 조각형의 쌍정 등 4가지 형태로 나눌 수 있다(Burkhard, 1993). 연구지역 PC2와 PC4, 2 시료에서는 직선형 쌍정, 곡선형 쌍정, 조각형 쌍정이 모두 관찰되지만, 특히 조각형 쌍정의 발달이 두드러지게 나타난다. PC3과 PC5의 시료에서는 직선형 쌍정만이 관찰되는데 넓은 직선형 쌍정의 발달이 우세하게 나타난다. PC6과 PC7의 시료에서는 직선형 쌍정과 조각형 쌍정이 관찰되는데 넓은 직선형 쌍정이 주종을 이루며 발달해 있다. Fig. 6은 본 연구지역에서 관찰된 방해석 쌍정의 대표적인 형태를 보여준다. 시료에서 관찰되는 방해석 입자들의 크기는 약 50 µm 이상에서 1,000 µm 이하이며, 쌍정을 측정하는데 가장 적당한 방해석 입자의 크기인 약 50~1,000 µm 범위로 다른 연구에서 보고된 것과 일치한다(Evans and Groshong, 1994).

Fig. 6.

Microphotographs of one or two twin sets observed in study area.

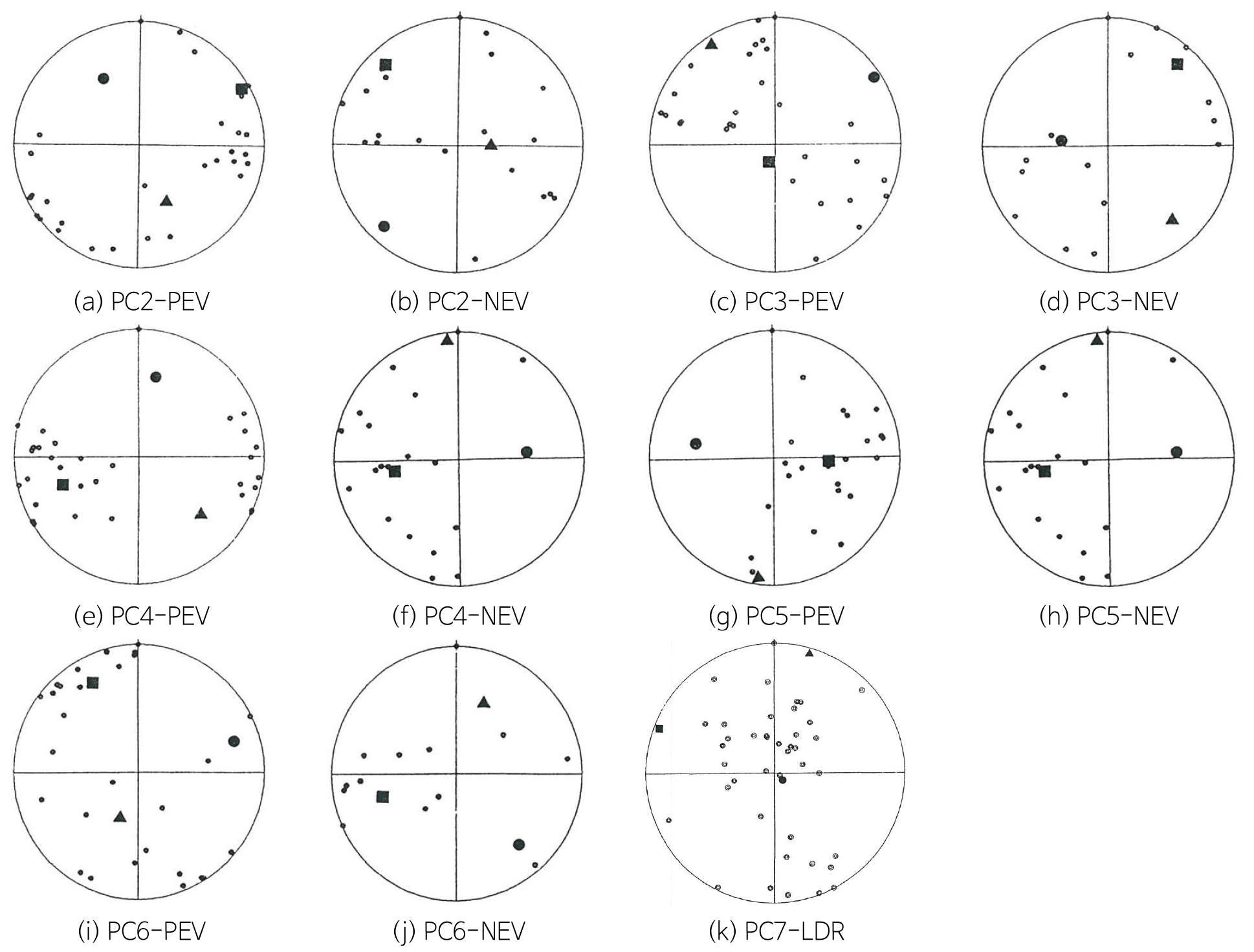
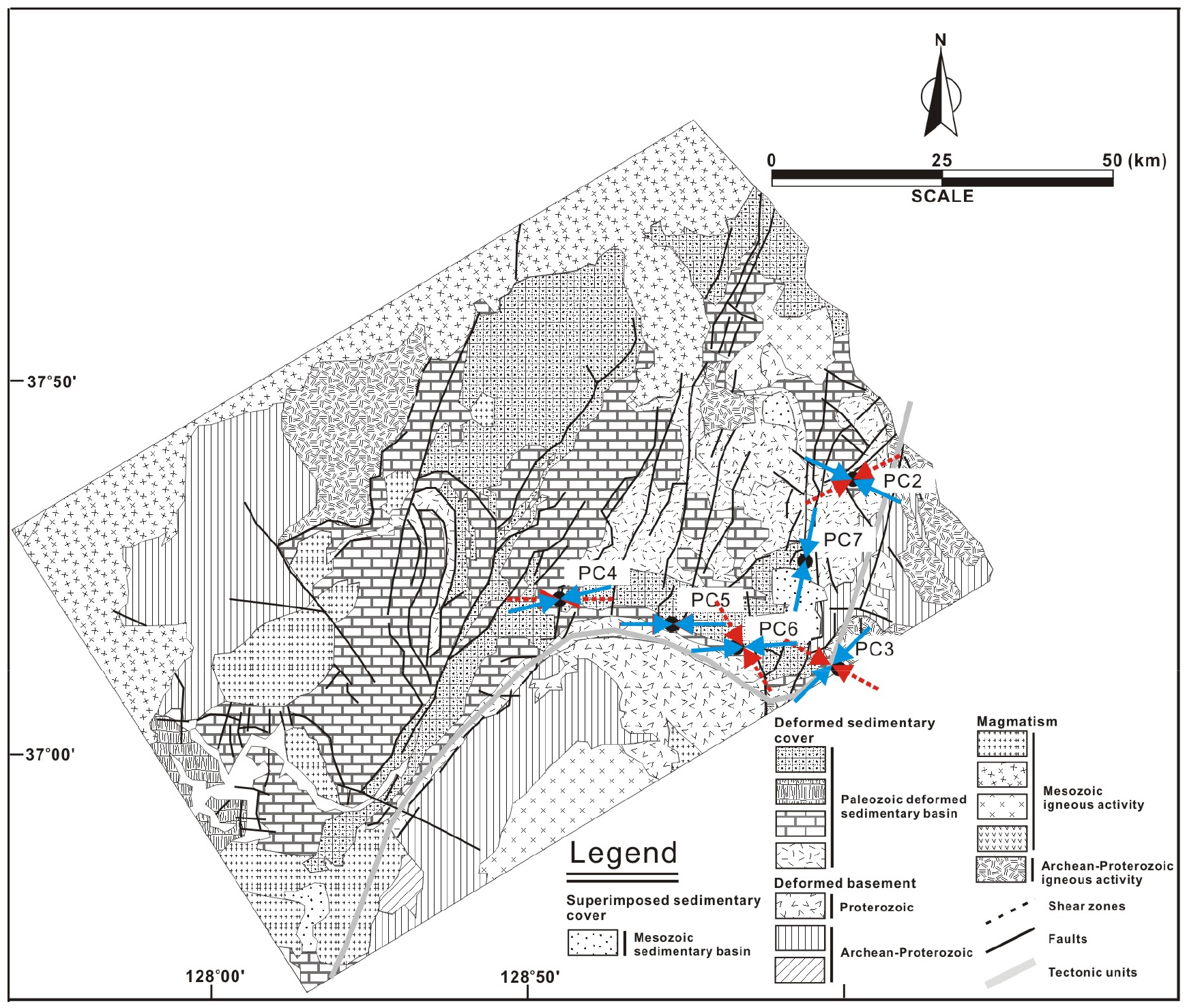
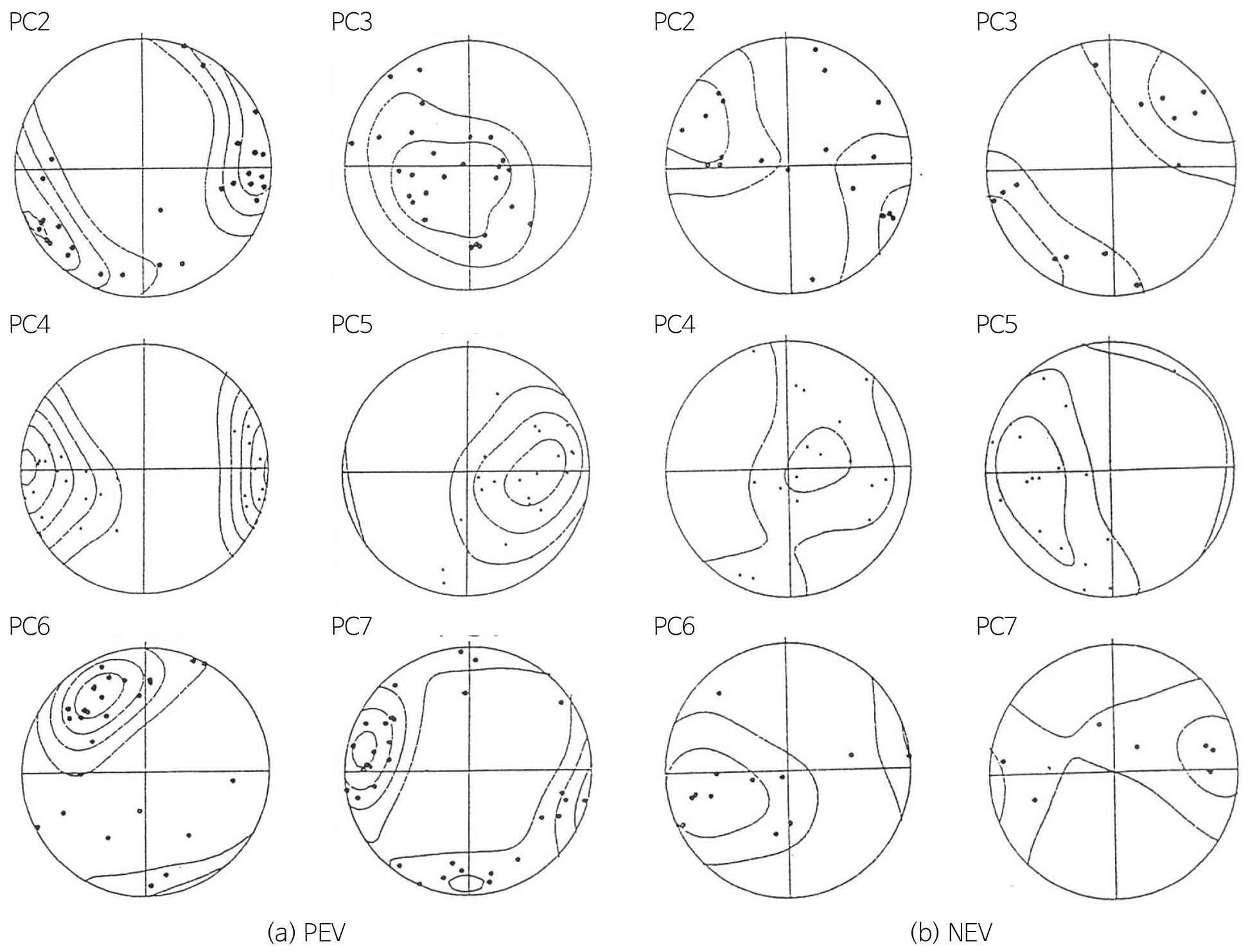
CSG 프로그램에 의한 변형률 분석결과는 Table 1과 같다. 변형률은 1.09~15.36% 범위를 보이나 대부분의 시료에서 1~3%의 범위를 보여 매우 낮은 변형률을 나타낸다. 쌍정의 평균 두께는 0.53~3.72 µm이나 PC2 시료를 제외한 모든 시료에서 1.8 µm 이하의 두께를 보이고, 쌍정의 치밀도는 21~53.1 쌍정/mm이다. Fig. 7은 CSG 프로그램에 의해 분석된 응력을 평사투영한 것으로 최대주응력, 중간주응력 및 최소주응력의 방향을 보여준다. 응력의 방향은 대부분의 시료에서(PC2, PC3, PC4, PC5 및 PC6) 두 방향의 압축응력을 보이며, PC7 시료에서만 한 방향의 압축응력을 보여주어 최소한 두 번 이상의 고응력장이 작용하였음을 지시한다. Fig. 8은 각 시료에서 측정된 압축응력의 방향을 시료 채취지점에 표시한 것으로 WNW-ESE~ENE-WSW의 방향성이 가장 우세하고 NW-SE 및 NE-SW의 방향성도 나타난다. 압축응력의 전체적인 방향성은 Fig. 9에서 보인다. Fig. 9a는 한 방향의 압축응력을 보이는 시료(Table 1의 LDR로 표시된 시료)와 두 방향의 압축응력을 보이는 시료에서 PEV를 보이는 쌍정에서 계산된 압축응력 방향을 도시한 것이고, Fig. 9b는 한 방향의 압축응력을 보이는 시료(Table 1의 LDR로 표시된 시료)와 두 방향의 압축응력을 보이는 시료에서 NEV를 보이는 쌍정으로부터 계산된 압축응력 방향을 도시한 것으로 방향의 차이가 거의 없다.

Fig. 7.

Equal area streographic projection of the stresses. ■, ● and ▲ represent the compression, intermediate and extension stresses, respectively.

Fig. 8.

Orientations of the compressive stress measured from calcite twins. Solid and dotted arrows indicate PEV and NEV of each samples, respectively.

Fig. 9.

Contour diagrams showing the directions of compression measured from twins of (a) PEV and (b) NEV.

방해석 쌍정 생성온도

평균 쌍정의 두께와 집중도는 각 시료에서 변형율 크기를 계산하기 위하여 사용된 쌍정 셑 평균에 근거하여 계산되며, 쌍정의 두께와 집중도에 있어서 변화는 자연적으로 변형된 조립질 입자를 갖는 석회암에서 쌍정의 변형율과 변성작용에 일치한다. 쌍정의 두께는 생성 당시의 온도와 밀접한 관계를 보이며 동일한 전단변형에 대하여 낮은 온도에서는 여러 개의 좁은 두께의 쌍정이 생성되는 반면 높은 온도에서는 몇 개의 넓은 두께의 쌍정이 생성된다(Burkhard, 1993). 실험실에서 인위적으로 생성시킨 쌍정의 경우 저온에서 변형된 쌍정의 두께는 5 µm 미만이며(Groshong, 1972), 300°C나 그 이상의 고온에서 변형된 쌍정의 두께는 5 µm 이상이고 입자 경계면 쪽으로 갈수록 좁아지는 렌즈 모양을 보이는데(Schmid et al., 1980) 실제 암석에서 렌즈 모양은 거의 관찰되지 않는다. Ferrill(1991)은 프랑스 동북부의 Northern Subalpine Chain 석회암층에서 쌍정의 생성온도를 추정하였는데 vitrinite reflectance, illite crystallinity 및 변성광물의 자료에 의하여 밝혀진 네 지역을 선정하여 각 지역에서 측정된 쌍정의 변형율, 평균 쌍정의 두께, 그리고 평균 쌍정의 치밀도 등의 관계를 이용하여 쌍정의 생성온도를 추정하였다. Ferrill에 의하면 쌍정의 변형율은 약 200°C까지는 10% 이하로 거의 변화가 없는 반면 그 이상의 온도에서는 10% 이상의 값을 보인다. 쌍정의 치밀도는 분산된 형태를 보이나 150°C 이상에서는 50 twin/mm 이하의 값을 보이며, 평균 쌍정의 두께는 150°C 이하에서는 1 µm 이하 150~200°C 사이에서는 1~3 µm 정도, 200°C 이상에서는 3 µm 이상의 값을 보임으로써 온도에 의한 영향을 잘 보여준다.

본 연구에서도 이들의 관계를 적용하여 온도 추정을 시도하였으며, 측정된 쌍정의 두께, 치밀도 및 변형률은 Table 1에 나타나 있다. PC2 시료는 2.15~3.72 µm 두께와 9.66~10.17% 변형율, 약 40 twin/mm의 집중도를 보여 온도는 200~300°C 범위로, PC4 시료는 0.55~1.82 µm 두께, 2.20~7.13% 변형율, 46 twin/mm 이상의 집중도를 보여 온도는 150~200°C 범위로 추정된다. PC3 시료는 0.44~0.70 µm 두께, 0.98~2.24% 변형율, 48 twin/mm 이상의 집중도를, PC5 시료는 0.47~1.31 µm 두께, 1.23~3.01% 변형율, 30 twin/mm 이상의 집중도를, PC6시료는 1.0~1.15 µm 두께, 1.58~2.26% 변형율, 20 twin/mm 이상의 집중도, 그리고 PC7시료는 0.23~0.51 µm 두께, 0.96~1.16% 변형율과 약 40 twin/mm의 집중도를 보여 이들 4개 시료에서의 온도는 170~200°C 이하로 추정된다(Fig. 10).

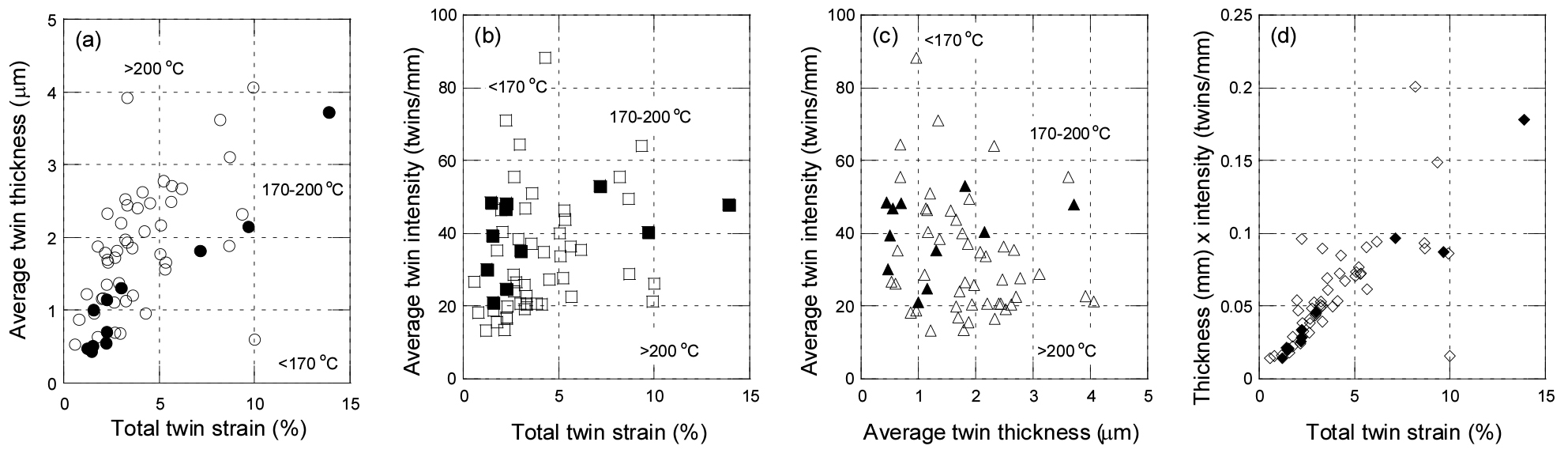
Fig. 10.

Estimation of deformation temperature from strain, thickness and intensity of twins. (a) Average twin thickness versus total twin strain, (b) average twin intensity versus total twin strain, (c) average twin intensity versus average twin thickness, and (d) product of average twin thickness and average twin intensity versus total twin strain.

고응력장

옥천습곡대 북동부 지역에 대한 고응력장의 연구는 현재까지 미미한 상태이나, Koh(1995)는 괴산지역의 옥천습곡대 지질구조를 통한 고응력장의 연구에서 트라이아스 말기에는 E-W, 쥬라기 초기에서 중기의 기간에는 NW-SE, 백악기 말기에는 N-S 방향의 주응력이 작용하였다고 주장하였다. Kim et al.(1996)은 태백지역에 인근한 여랑-임계지역의 지질구조를 연구하여 조산누층군에는 4번의 변형작용이 있었으며, 북서-남동 방향의 선구조 및 습곡구조들은 송림조산운동 기간에 생성된 후 대보조산운동 시기에 경사가 더욱 급해졌으며, 쥬라기 말~백악기 초의 단층운동과 백악기 말~제 3기 초의 불국사 조산운동 기간에 동-서 방향의 습곡구조 및 드러스트 단층이 생성되었다고 주장하였다. 또한 Jang and Gim(1996)과 Jang(1994)는 옥천습곡대 및 경기육괴내의 중생대의 화강암에 분포하는 아문 미세균열 및 유체포유물의 측정을 통하여 180 Ma 이전에는 E-W의 최대수평주응력이, 180~100 Ma 사이의 기간에는 NW-SE의 최대수평 주응력이 작용하였으나, 100 Ma 이후에는 최대 수평주응력의 방향이 N-S 회전하였다고 발표하였다.

본 연구의 방해석 쌍정에서 측정된 고응력장은 E-W 방향의 최대주응력이 가장 우세하게 작용하였고 부분적으로 NW-SE의 최대주응력 및 NE-SW의 최대주응력이 작용하여 위의 여러 연구와 비교할 때 대부분의 쌍정은 트라이기말에서 쥬라기의 송림조산운동 기간중에 생성된 것으로 사료된다. 그러나 쥬라기 기간의 대보조산운동과 백악기의 불국사 변동도 풍촌 석회암의 방해석에 쌍정을 생성하였고 그 크기는 비슷한 것으로 판단된다.

결 론

조선누층군 두위봉형의 풍촌석회암층에서 6개의 시료를 채취하여 방해석 c-축의 방향 및 경사, e 쌍정면의 방향 및 경사, 쌍정의 평균 두께 및 갯수, 방해석 입자의 크기 등을 측정하였다. 측정된 자료들은 Calcite Strain Gauge(CSG) 프로그램에 입력되어 쌍정의 변형률, 평균 두께, 치밀도 및 고응력장의 상대적 크기 및 방향 등을 계산하였다. 쌍정의 변형률은 1.09~15.36%, 평균 두께는 0.53~3.72 µm, 치밀도는 21~53.1 twin/mm의 범위를 보인다. 쌍정의 변형률, 치밀도 및 두께에 의한 변성온도 계산결과 대부분의 시료에서 170~200°C 이하를 보여, 풍촌층의 상부층인 직운산층의 변성온도에 비교할 때 최대 심도의 1/2 이상 상승한 후에 쌍정이 생성된 것으로 판단된다. 응력장의 방향은 5개의 시료에서 2방향을 보이는 반면, 단지 1개의 시료에서만 한 방향을 보여 대부분의 시료에서 압축응력이 2번 이상 작용하였음을 보여준다. 압축응력은 WNW-ESE~ENE-WSW의 방향성이 가장 우세하고 NW-SE와 NE-SW의 방향성도 보인다. 본 연구에서 측정된 고응력장과 연구지역 인근에서 지질구조나 다른 방법에 의하여 규명된 고응력장과 비교할 때 E-W 방향의 고응력장은 트라이아스기 말에서 쥬라기 초에 발생한 송림조산운동에 가장 큰 압축응력이 작용하였고 쥬라기에 발생한 대보조산운동과 불국사 변동에 의해서도 쌍정이 생성된 것으로 판단된다.