New Joint Roughness Coefficient and Shear Strength Criterion Based on Experimental Verification of Standard Roughness Profile

Hyun-Sic Jang; Min-Yong Sim; Bo-An Jang

doi:10.9720/kseg.2021.4.561

Preview

Research Article

The Journal of Engineering Geology. 31 December 2021. 561-577
https://doi.org/10.9720/kseg.2021.4.561

New Joint Roughness Coefficient and Shear Strength Criterion Based on Experimental Verification of Standard Roughness Profile

표준 거칠기 단면의 실험적 검증에 의한 새로운 거칠기 계수 및 전단강도 기준식

Hyun-Sic Jang¹

Min-Yong Sim²

Bo-An Jang³^*

장 현식¹

심 민용²

장 보안³^*

¹Research Professor, Research Institute for Earth Resources, Kangwon National University

²Master Student, Department of Geophysics, Kangwon National University

³Professor, Department of Geophysics, Kangwon National University

¹강원대학교 지구자원연구소 연구교수

²강원대학교 지구물리학과 석사과정

³강원대학교 지구물리학과 교수

^{*Corresponding Author}

ABSTRACT

The ten standard roughness profiles suggested by Barton and Choubey (1977) were extended to make three-dimensional (3D) joint models whose profiles were identical at any cross section. Replicas of joint models were produced using plaster of Paris, and direct shear tests were performed to verify the joint roughness coefficients (JRC) of the standard roughness profiles. Joint shear strengths measured by direct shear tests were compared with those predicted by the shear failure criterion suggested by Barton (1973) based on JRC, joint compressive strength (JCS), and joint basic friction angle ( $ϕ_{b}$ ). Shear strengths measured from joints of the first and fourth standard roughness profiles were close to predicted values; however, shear strengths measured from the other joint models were lower than predicted, the differences increasing as the roughness of joints increased. Back calculated values for JRC, JCS, and from the results of the direct shear tests show measured shear strengths were lower than predicted shear strengths because of the JRC values. New JRC were back calculated from the measured shear strength and named JRC_m. Values of JRC_m were lower than the JRC for the standard roughness profiles but show a strong linear relationship to JRC. Corrected JRC_m values for the standard roughness profiles are provided and revised relationships between JRC_m and JRC, and new shear strength criterion are suggested.

Keywords

rock joint

shear strength criterion

joint roughness coefficient (JRC)

joint replica

direct shear test

back analysis

Barton and Choubey(1977)가 제안한 10개의 표준 거칠기 단면을 3차원으로 확장하여 모든 단면의 거칠기가 일정한 3차원 표준 거칠기 절리 모형을 제작하였다. 석고를 사용하여 이 절리 모형을 복제하여 절리시료를 제작하였고, 복제된 절리시료에 직접전단시험을 실시하여 표준거칠기 단면에 부여된 절리 거칠기계수(JRC)를 검증하였다. 먼저 절리 시료의 JRC, 절리면압축강도(JCS)와 기본마찰각( $ϕ_{b}$ )을 이용하여 Barton (1973)의 전단강도 기준식에서 절리의 전단강도를 추정하고, 직접전단시험에서 측정된 전단강도와 비교하였다. 직접전단시험에서 측정된 전단강도는 1번과 4번 표준 거칠기를 제외한 8개 시료에서 Barton의 기준식에서 추정된 전단강도보다 낮았고, JRC가 큰 시료에서 차이가 더욱 크게 나타났다. 직접전단시험 결과를 역해석하여 JRC, JCS 그리고 $ϕ_{b}$ 의 적절성을 검토하였고, JRC의 문제점으로 인하여 측정된 전단강도가 추정된 전단강도보다 낮은 것으로 판명되었다. 역해석으로 구한 표준 거칠기 단면의 JRC 값인 JRC_m은 JRC보다 전반적으로 낮은 값을 보이지만 JRC와 상관성이 매우 높은 직선의 관계를 나타내었다. 위의 결과를 종합하여 표준 거칠기 단면의 정확한 JRC_m을 제시하였고, JRC_m과 JRC의 상관관계를 제시하였으며, Barton의 전단강도 기준식을 수정하여 제안하였다.

키워드

절리면

전단강도

절리 거칠기 계수

복제 절리시료

직접전단시험

역해석

MAIN

서 론
복제절리의 제작
석고의 기본마찰각 측정
직접전단시험
절리면압축강도(JCS)의 역산
기본마찰각( $ϕ_{b}$ )의 역산
절리 거칠기 계수(JRC)의 역산
표준 거칠기 단면의 정확한 거칠기 계수 결정
통계적 변수 Z₂와 역산된 JRC_m의 상관관계
Barton의 전단강도 기준식의 수정 및 검증
요약 및 결론

서 론

절리면의 전단강도는 무결암의 강도에 비하여 현저히 낮기 때문에 암반의 거동을 좌우하는 중요한 특성 중의 하나이다. 절리면의 전단강도는 절리가 파괴될 때 작용하는 최대 전단응력으로 정의되며 절리면에 작용하고 있는 수직응력의 함수이다. Mohr-Coulomb은 전단강도를 수직응력에 대하여 직선의 관계로 표현하였으며, 절리가 파괴될 때 작용하는 전단응력( $τ$ )과 수직응력( $σ$ )의 관계를 식 (1)과 같이 나타내었다.

(1)

τ = c + σ \tan ϕ

여기서, $c$ 는 절리의 점착력이고, $ϕ$ 는 절리의 마찰각이다. 이 관계식은 간단하고, $c$ 와 $ϕ$ 의 2개의 변수로 절리의 거동이 규정되기 때문에 현재까지도 널리 사용되고 있다. 마찰각 $ϕ$ 는 절리면의 형상, 즉 절리면의 돌기(asperity) 분포나 거칠기, 돌기의 강도 등의 영향을 받는 변수이다. 낮은 수직응력하에서 절리가 미끄러질 때에는 절리의 상반이 돌기의 경사를 타고 올라가서 돌기의 형상이 유지되는 반면에, 수직응력이 높아지면 돌기가 파괴되면서 절리면의 형상이 변하게되고, 이에 따라 $ϕ$ 도 변하게 된다. 그러므로 Patton(1966)은 일정한 수직응력( $σ_{T}$ )보다 낮은 수직응력이 작용하면 절리의 상반이 돌기의 경사를 타고 올라가서 마찰각 $ϕ$ 는 기본마찰각( $ϕ_{b}$ )과 돌기의 경사각( $i$ )의 합으로 나타나고, 절리면에 작용하는 수직응력이 $σ_{T}$ 보다 크면 절리면이 미끄러지는 동안 돌기가 파괴되어 편평하게 되므로 마찰각은 잔류마찰각 $ϕ_{r}$ 과 일치하게 되어, 절리면의 전단강도를 식 (2)와 같은 이중 직선의 식으로 나타내었다.

(2)

τ = σ \tan (ϕ_{b} + i) σ ≺ σ_{T} τ = c_{j} + σ \tan ϕ_{r} σ \geq σ_{T}

여기서, $c_{j}$ 는 겉보기 점착력이다. 이러한 이중 직선의 전단강도 관계식은 Mohr-Coulomb의 직선 관계식보다는 좀 더 정확하게 전단강도를 표현할 수 있으나, 수직응력이 $σ_{T}$ 에서 점차 증가하면 더 많은 돌기가 파괴되고 분쇄되어 절리면의 형상은 지속적으로 변하게 되고, 전단강도도 계속 변하게 된다. 많은 연구자들이 위와 같은 현상 때문에 전단강도가 수직응력에 대하여 곡선의 관계를 보일 것으로 이해하고 있었고(Lane and Heck, 1964; Patton, 1966; Byerlee, 1967), Ladanyi and Archambault(1970)가 처음으로 곡선의 관계식을 제안하였다. 그러나 이 관계식은 측정하기 매우 어려운 변수를 포함하고 있어서 실질적으로 사용되지 못하였다. Barton(1973)은 절리거칠기계수(Joint Roughness Coefficient, JRC), 절리면압축강도(Joint Compressive Strength, JCS)와 기본마찰각( $ϕ_{b}$ )을 사용한 곡선의 관계식을 제안하였으며, 비교적 측정하기 쉬운 변수를 사용하여 이해하기 쉽고 간단한 형태로 관계식을 표현하여 현재도 널리 사용되고 있다(식 (3)).

(3)

τ = σ_{} \tan [J R C ∙ \log (\frac{J C S}{σ_{}}) + ϕ_{b}]

Barton and Choubey(1977)는 136회의 절리면 전단시험으로부터 JRC를 역해석하여 10개의 표준 거칠기 단면을 제안하고(Table 1), 시료의 거칠기 단면을 표준 거칠기 단면과 육안으로 비교하여 JRC를 결정하는 시험법을 제안하였다. 이후, 국제암반역학회(ISRM)는 이 JRC 측정법을 표준시험법으로 채택하였으나 이 방법은 거칠기를 육안으로 비교하기 때문에 측정자의 숙련도나 주관에 따라 JRC 값의 오차가 많이 발생하는 문제점이 있다(Hsiung et al., 1993). 이러한 문제점을 해결하기 위해 많은 연구자들은 표준 거칠기 단면을 수치화하여 통계적 방법이나 프랙탈 차원을 이용하여 JRC를 정량적으로 결정하는 방법을 제안하였다(Tse and Cruden, 1979; Maerz et al., 1990; Yu and Vayssade, 1991, Kulatilake et al., 1995; Jang et al., 2005, 2014). 표준 거칠기 단면은 2차원 형상으로 거칠기를 표현하지만 절리면의 거칠기 형상은 3차원이므로, Grasselli et al.(2002)과 Grasselli and Egger(2003)를 비롯한 여러 연구자들이 3차원 거칠기를 사용하여 절리면의 전단강도 관계식을 연구하고 제안하였으나, 변수가 복잡하며 측정이 어려워 현재에는 거의 사용되고 있지 않다(Belem et al., 2000; Yang and Chiang, 2000; Park and Song, 2013).

Barton의 관계식을 사용하여 절리면의 전단강도를 정확하게 추정하기 위해서는 JRC를 정확하게 측정하여야 한다. 그러나 JRC는 절리면의 일부분인 1차원의 선을 따라 측정되므로, 전단강도에 영향을 미치는 전체 절리면을 대표하기에는 문제가 있다. Fig. 1은 Jang et al.(2010)의 연구에서 사용된 시료의 절리면 형상과 이 절리면에 30개의 선을 따라 측정된 JRC를 보여준다. 가장 거친 단면을 따라 측정된 JRC는 20.0이며 가장 편평한 단면의 JRC는 9.7로, 하나의 시료 내에서도 단면의 위치에 따라 아주 큰 JRC의 차이를 보여준다. 이러한 큰 차이는 Hsiung et al.(1993)의 연구에서도 발견되어, 특정 시료에서 측정된 JRC가 0에서 20까지 변하는 절리면도 있음을 보고하였다. Jang et al.(2010)과 Hsiung et al.(1993)은 이러한 절리면의 전단강도를 추정하기 위한 JRC 값으로 여러 단면에서 측정된 JRC의 평균을 사용하도록 제안하였으나, 절리면 직접전단시험에서 측정된 전단강도를 역산하여 구한 JRC와 JRC의 평균이 차이가 있음을 보고하였다(Wang et al., 2016, 2018, 2019; Liu et al., 2017; Fan and Cao, 2020).

Table 1.

Standard roughness profiles suggested by Barton and Choubey (1977). The numbers within parentheses are the exact JRC values

Profile No.	Rock type	Typical roughness profiles	JRC
1	Slate		0~2 (0.4)
2	Aplite		2~4 (2.8)
3	Gneiss (muscovite)		4~6 (5.8)
4	Granite		6~8 (6.7)
5	Granite		8~10 (9.5)
6	Hornfels (nodular)		10~12 (10.8)
7	Aplite		12~14 (12.8)
8	Aplite		14~16 (14.5)
9	Hornfels (nodular)		16~18 (16.7)
10	Soapstone		18~20 (18.7)

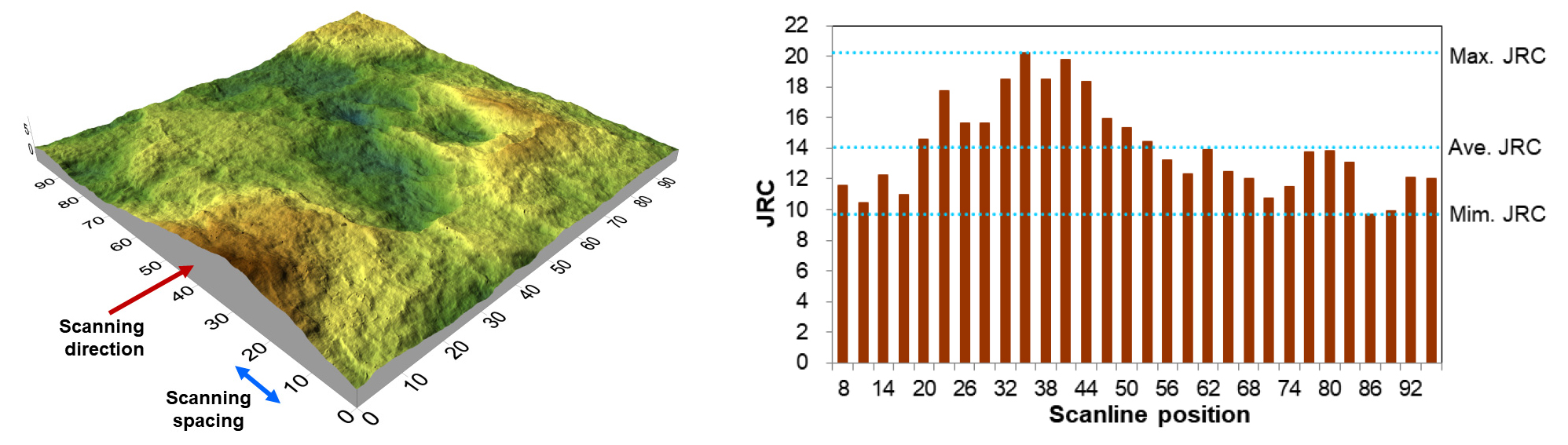
https://static.apub.kr/journalsite/sites/kseg/2021-031-04/N0520310409/images/kseg_31_04_09_F1.jpg

Fig. 1.

(a) Three-dimensional profile of a joint showing different roughness according to the scanning lines. (b) Joint roughness coefficients (JRC) measured along 30 different scanning lines (Jang et al., 2010).

비록 절리면의 JRC는 동일하더라도, 하나의 시료 내에서 단면의 위치에 따라 JRC 값이 큰 차이가 나는 절리면의 전단강도와 전체 단면의 JRC가 비슷한 절리면의 전단강도가 서로 일치하지는 않을 것으로 판단된다. 이에 따라 이 연구에서는 전단강도에 미치는 JRC의 영향을 정확하게 파악하기 위하여 모든 단면의 JRC가 동일한 시료를 제작하였다. 먼저 Barton and Choubey(1977)가 제안한 10개의 표준 거칠기 단면의 수치화 자료를 3차원 모델링 프로그램을 이용하여 모든 단면의 형상이 동일한 절리면의 3차원 수치화 자료를 작성하였다. 이 수치화 자료를 바탕으로 정밀한 3차원 프린터(3D Printer)를 사용하여 3차원 표준 거칠기 모형을 제작하였고, 실리콘을 이용하여 각 모형의 형틀을 제작한 후 역학적 특성이 서로 다른 세 종류의 석고를 사용하여 절리 모형을 복제하였다. 복제된 절리에 직접전단시험을 실시하여 측정된 전단강도로부터 JRC 값을 역해석하여 표준거칠기 단면의 JRC 값과 비교하였다. 역해석으로 구해진 JRC 값은 표준거칠기 단면에서 주어진 값과 차이를 보여, 표준거칠기 단면에 부여된 JRC 값은 수정될 필요가 있음을 파악하였다. 이 연구를 바탕으로 각각의 표준거칠기 단면에 새로운 JRC 값을 부여하였으며, 통계적 변수 $Z_{2}$ 를 사용하여 JRC를 구하는 상관관계 식과 Barton의 전단강도 기준식을 수정한 새로운 전단강도 기준식을 제안하였다.

복제절리의 제작

Jang et al.(2014)은 Barton and Choubey(1977)가 제시한 10개의 표준 거칠기 단면을 0.1 mm 간격으로 정밀하게 수치화하여 여러 종류의 거칠기 변수와 거칠기 계수(JRC)와의 상관관계를 연구하였고, 이 연구에서는 Jang et al.(2014)이 수치화한 표준 거칠기 단면의 수치자료를 사용하였다. 표준 거칠기 단면은 2차원 형상이므로, 3차원 모델링 프로그램(Rhinoceros)을 이용하여 거칠기 단면에 직각 방향(Fig. 2a의 z 방향)으로 표준 거칠기 단면을 연장하여 가로가 약 10 cm 세로가 약 10 cm이고, 모든 단면(Fig. 2의 X-Y 단면)의 거칠기 형상이 동일한 절리면의 수치화 자료를 형성하였다(Fig. 2a). 이 수치화 자료를 이용하여 0.12 mm의 정밀도와 0.05 mm의 층 두께로 출력이 가능한 3D 프린터를 사용하여 3차원 절리 모형을 제작하였다(Fig. 2b). 3D 프린터로 제작된 절리 모형의 정확성을 검정하기 위하여 3차원 레이저 스캐너(laser scanner)를 이용하여 각각의 절리 모형에서 15 mm 간격으로 6개의 단면을 측정하였다. 각 단면에서 $Z_{2}$ 를 구한 후, Jang et al.(2014)이 제시한 $Z_{2}$ 와 JRC의 관계식 $J R C = 55.61 (Z_{2})^{0.416} - 17.6$ 을 사용하여 각 표준 거칠기 단면의 JRC 값을 계산하였다(Table 2). 모든 절리 모형의 JRC 값은 Barton and Choubey(1977)와 Jang et al.(2014)이 제시한 JRC 값과 ±1 이내로 유사하나, 4번 단면의 절리 모형에서 측정된 JRC 값은 Barton and Choubey(1977)가 제시한 값과는 상당한 차이를 보인다. 이는 Barton and Choubey(1977)가 제시한 JRC 값은 경험적 모델로부터 도출된 것이므로 거칠기 형상에 대한 통계적 파라미터로부터 결정된 JRC와 차이를 보이는 것으로 판단되며, 이미 여러 연구에서 같은 연구결과를 발표한 바 있다(Tse and Cruden, 1979; Yu and Vayssade, 1991; Kulatilake et al., 1995, Jang et al., 2005).

https://static.apub.kr/journalsite/sites/kseg/2021-031-04/N0520310409/images/kseg_31_04_09_F2.jpg

Fig. 2.

(a) Three-dimensional joint model produced by digitized values of the eighth standard roughness profile. (b) Joint model produced by a 3D printer from the digitized 3D joint model.

Table 2.

JRC values suggested by Barton and Choubey (1977) and Jang et al. (2014), and those measured from joint models produced by 3D printer

Profile No.	1	2	3	4	5	6	7	8	9	10
JRC (Barton and Choubey, 1977)	0.4	2.8	5.8	6.7	9.5	10.8	12.8	14.5	16.7	18.7
JRC (Jang et al., 2014)	0.14	3.24	5.06	9.33	9.79	9.68	12.87	13.58	15.45	19.55
JRC (joint model)	0.03	3.35	5.18	8.34	9.61	10.30	12.01	14.47	15.98	19.35

3D 프린터로 제작된 절리 모형에 실리콘을 부어 절리 모형의 형틀(mold)을 제작한 후, 암석과 유사한 취성 특성을 보이는 석고를 사용하여 절리 모형을 복제하였다. 다양한 수직응력하에서 정확한 절리면 전단강도를 구하기 위해서는 동일한 형상을 가진 여러 개의 절리면이 필요하지만 암반에서 여러 개의 동일한 절리를 채취하는 것은 불가능하다. 그러나 절리를 복제하면 동일한 형상을 가진 여러 개의 절리를 제작할 수 있으므로, 절리면 전단강도 연구에 복제절리가 많이 사용되었다(Kulatilake et al., 1995; Grasselli and Egger, 2003; Jang et al., 2014). 이 연구에서는 강도에 의한 영향을 고려하기 위하여 주식회사 문교산업에서 생산되는 GM-10, Dental Stone 그리고 Diestone 등 물리적, 역학적 특성이 서로 다른 세 종류의 석고를 사용하였다. 석고와 물의 배합비는 제조사에서 제시한 표준혼수량(GM-10 40%, Dental Stone 24%, Dieston 21%)를 적용하였으며 제작된 시료들은 약 2개월의 양생기간 이후에 시험에 사용하였다.

석고의 물리적, 역학적 특성은 Table 3과 같다. 밀도는 1.55~1.93 g/cm³, 일축압축강도는 34.3~92.6 MPa, 탄성계수는 11.5~25.1 GPa 그리고 포아송 비는 0.25~0.29의 범위를 보인다. 모든 물리적, 역학적 특성에서 GM-10이 가장 낮은 값을 보이고, Diestone이 가장 높은 값을 보인다. 각각의 표준 거칠기 단면에 대하여, 또한 각각의 석고 종류에 대하여 5개의 절리가 복제되어 합계 150개의 복제 절리면 시료를 제작하였다.

Table 3.

Physical and mechanical properties of the plasters

Type of plaster	Dry density (g/cm³)	Uniaxial Compressive Strength, UCS (MPa)	Young’s Modulus, E (GPa)	Poisson’s Ratio, 𝜈
GM-10	1.55	34.3	11.5	0.25
Dental Stone	1.74	58.7	19.2	0.27
Diestone	1.93	92.6	25.1	0.29

석고의 기본마찰각 측정

기본마찰각( $ϕ_{b}$ )은 Barton의 전단강도 관계식에 포함되어있는 변수이므로, 절리면의 전단강도를 정확하게 추정하기 위해서는 꼭 필요한 특성이다. 기본마찰각은 풍화되지 않은 평편한 면에서 측정되는 암석의 고유한 특성 중의 하나로, 직접전단시험이나 기울임시험, 당김 시험을 이용하여 측정할 수 있다. 국제암반역학회는 기울임 시험을 기본마찰각 측정의 표준시험법으로 채택하였으나(Alejano et al., 2018), 기울임 시험은 측정값의 분산이 심하여 당김시험이 더욱 개선된 방법이라는 반론도 있다(Stimpson 1981; Cruden and Hu 1988; González et al., 2014; Lee et al., 2019). 이 연구에서는 기울임 시험과 당김시험을 모두 시행하여 기본마찰각을 측정하였다. 기울임 시험은 국제암반역학회에서 제시한 방법에 따라 시행되었으며 GM-10의 $ϕ_{b}$ 는 33.8~38.2°의 범위, Dental Stone의 $ϕ_{b}$ 는 32.9~36.5°의 범위, 그리고 Diestone의 $ϕ_{b}$ 는 31.4~35.1°의 범위를 보여, 3.6~4.4°의 오차 범위를 보인다.

당김시험은 직접전단시험과 유사한 원리로 실시되는 시험으로, 시료를 시료 상자에 고정할 필요가 없어서 시험이 간편하다는 장점이 있는 반면에 시료에 작용하는 수직응력은 직접전단시험에 비하여 매우 낮다. 이 연구에서는 Lee et al.(2019)의 연구와 동일하게 정속모터를 사용하여 일정한 속도로 시료를 전단하고, 무게추를 사용하여 여러 단계의 수직응력을 가할 수 있는 당김시험기을 사용하여 시험을 시행하였다. 당김시험은 각 종류의 석고에 대하여 2~28 kPa의 수직응력을 적용하여 5회 실시되었고, 측정의 정확성을 위하여 4번 반복하여 시험을 실시하였다. 수직응력에 따른 전단응력 직선의 기울기가 기본마찰각이며, GM-10의 $ϕ_{b}$ 값은 36.05~37.32°, Dental Stone의 $ϕ_{b}$ 값은 36.85~37.76°, Diestone의 $ϕ_{b}$ 값은 37.03~38.31° 범위를 보였다. 각 석고에서 측정된 $ϕ_{b}$ 의 오차는 0.92°~1.28°로 매우 낮은 분산도를 나타내었다.

각 종류 석고의 기본마찰각을 결정하기 위하여 기울임 시험과 당김 시험에서 측정된 마찰각의 평균을 구하였다(Table 4). 기울임 시험에서 측정된 Dental Stone과 Diestone의 $ϕ_{b}$ 는 일축압축강도가 훨씬 낮은 GM-10 석고보다 낮은 값을 보이고, 측정값 또한 분산되어 신뢰도 낮다. 그러나 당김 시험에서 측정된 $ϕ_{b}$ 는 측정값이 일정하고, 또한 강도가 높은 Dental Stone과 Diestone의 $ϕ_{b}$ 가 GM-10의 $ϕ_{b}$ 보다 높은 값을 보여 신뢰성이 높은 것으로 판단된다. 그러므로 당김 시험에서 측정된 석고의 마찰각을 기본마찰각으로 결정하였고, GM-10의 $ϕ_{b}$ 는 36.4°, Dental Stone의 $ϕ_{b}$ 는 37.3°, 그리고 Diestone의 $ϕ_{b}$ 는 37.8°로 결정하였다.

Table 4.

Basic friction angles determined by the tilt test and the pull test

	GM-10	Dental Stone	Diestone
Tilt test ( $ϕ_{b}$ )	36.1°	34.4°	33.6°
Pull test ( $ϕ_{b}$ )	36.4°	37.3°	37.8°

직접전단시험

직접전단시험은 (주)에이스원에서 제작한 직접전단시험기를 사용하여 수행되었고, 이 시험기의 수직응력은 ±1% 오차로 제어가 가능하고 전단방향으로는 일정한 전단변위 제어가 가능하다(Fig. 3). 직접전단시험 시, 수직응력은 0.5 MPa, 1.0 MPa, 2.0 MPa, 3.0 MPa 그리고 4.0 MPa의 5단계를 적용하였고, 전단변위는 1.0 mm/min의 일정한 변위 속도가 유지되었다. 또한 전단시험동안 수직응력, 전단응력, 수직변위 그리고 전단변위가 실시간으로 기록되었다.

https://static.apub.kr/journalsite/sites/kseg/2021-031-04/N0520310409/images/kseg_31_04_09_F3.jpg

Fig. 3.

Direct shear test apparatus.

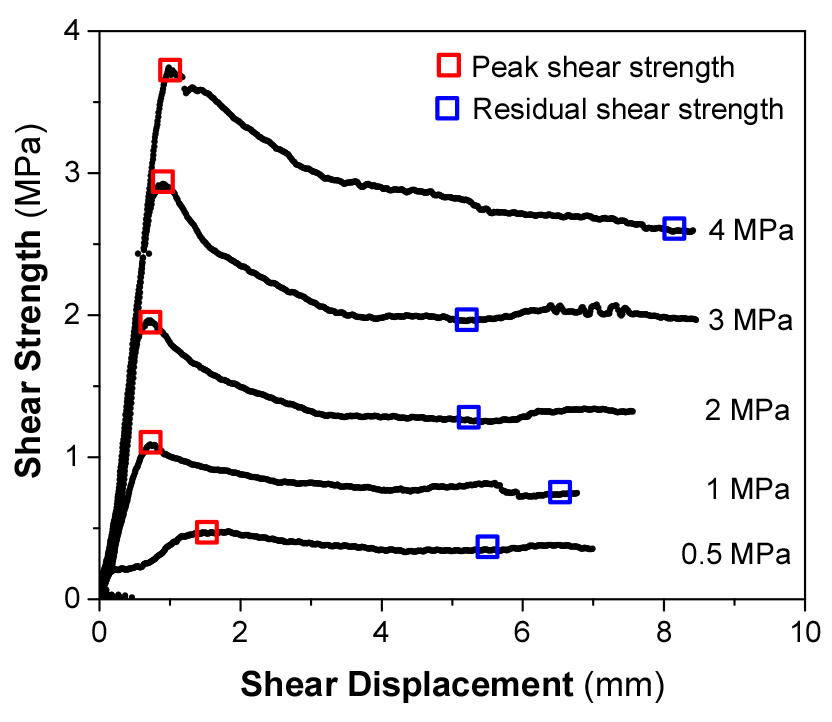
직접전단시험에서 측정된 전단응력은 전단변위가 증가함에 따라 증가하여 최대전단강도를 보인 후 감소하여 일정한 잔류전단강도를 보이고 있다(Fig. 4). 매우 낮은 수직응력에서는 최대전단강도가 뚜렷하지 않으나 수직응력이 증가하면 아주 뚜렷한 최대전단강도를 나타내고, 잔류전단강도는 약간의 오차는 있으나 비교적 일정한 응력을 보이고 있다. 수직응력이 증가함에 따라 최대전단강도와 잔류전단강도는 모두 증가하는 양상을 보인다.

https://static.apub.kr/journalsite/sites/kseg/2021-031-04/N0520310409/images/kseg_31_04_09_F4.jpg

Fig. 4.

Plot of shear stress versus shear displacement measured from replica joints of the fourth standard roughness profile using GM-10 plaster.

1번에서 10번까지의 표준거칠기 모형에서 직접전단시험을 실시하여 측정된 수직응력의 크기에 따른 최대 전단응력과 Barton(1973)이 제시한 절리면 전단강도기준 곡선을 함께 도시하였다(Fig. 5). 1번 표준거칠기 모형에서 측정된 전단응력은 수직응력과 거의 직선의 관계를 보이고 있으나, 거칠기가 증가할수록 전단응력은 수직응력에 대하여 곡선의 관계를 보이고 있다. 또한 1번 표준거칠기 모형에서 측정된 최대전단응력은 Barton의 강도기준과 거의 일치하지만, 2번 표준거칠기 모형에서부터 측정된 최대전단응력은 Barton의 강도기준에서 계산된 응력보다 낮고, 표준거칠기 단면의 번호가 증가할수록 차이는 점차 증가한다. 다만 4번 표준거칠기 모형에서 측정된 전단응력은 Barton의 강도기준식에 의한 전단강도와 비교적 일치한다. Barton and Choubey(1977)가 4번 표준거칠기 단면에 대하여 부여한 JRC 값은 거칠기 변수를 이용하여 계산한 JRC 값에 비하여 상당히 낮기 때문에 측정값과 계산값이 비교적 일치하는 것으로 판단된다(Table 1). 8번, 9번, 10번 표준거칠 모형 그래프에서 초기 낮은 수직응력 구간의 Barton의 전단강도 곡선이 곡선이 아닌 직선으로 표시된 것은 Barton(1973)의 전단강도기준에서 $\tan^{- 1} (τ / σ_{n})$ 값이 최대 70° 설정되어 있기 때문이다(Barton and Choubey, 1977). 따라서 원점을 지나고 각도가 70°인 직선을 기준으로 왼쪽에는 전단강도 곡선이 존재하지 않고 오른쪽에만 전단강도 곡선이 존재하게 된다.

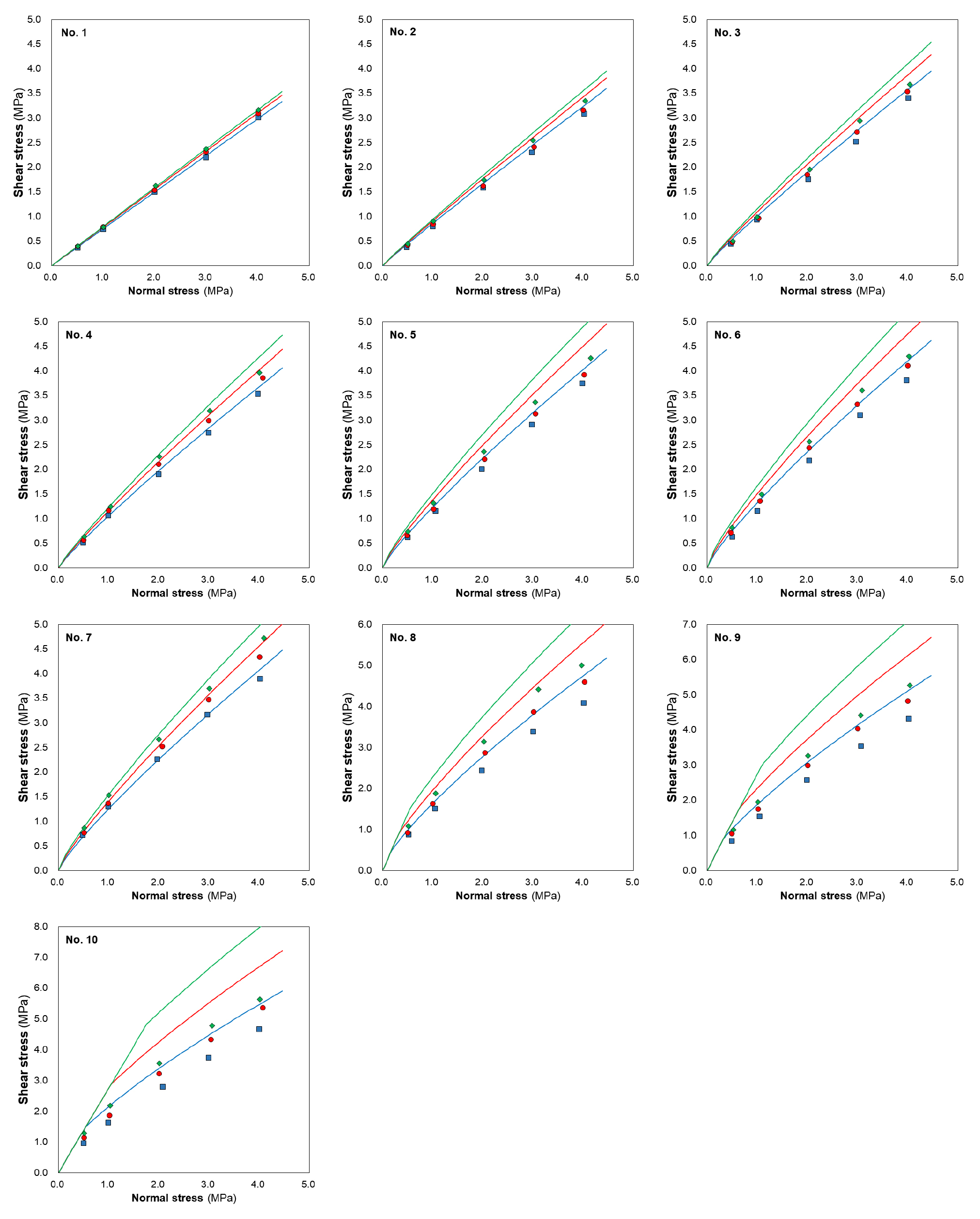
https://static.apub.kr/journalsite/sites/kseg/2021-031-04/N0520310409/images/kseg_31_04_09_F5.jpg

Fig. 5.

Shear stresses measured by direct shear tests for GM-10 (◆), Dental Stone (●), and Diestone (■). Solid lines represent Barton’s failure criterion (Barton, 1973) for three types of plaster: GM-10 (green); Dental Stone (red); and Diestone (blue).

표준 거칠기 모형에서 측정된 전단응력이 Barton의 전단강도 기준식( $τ = σ_{n} \tan [J R C ∙ l o g (J C S / σ_{n}) + ϕ_{b}]$ ) 에서 계산된 전단응력과 차이를 보임은 전단강도 식 내에 있는 변수의 측정과 사용에서 오차가 있음을 지시한다. 즉, JRC, JCS 그리고 $ϕ_{b}$ 중의 일부 혹은 모든 변수에서 문제가 있을 수도 있으므로, 전단강도 기준식 내의 세 변수의 적정성과 오차를 역해석을 통하여 분석하였다. 변수의 적정성은 먼저 두 개의 변수는 참으로 가정하고, 나머지 한 개의 변수의 적정성을 검토하는 방법으로 진행하였다. 예를 들면, JCS의 적정성을 검토할 때에는 JRC와 $ϕ_{b}$ 는 참값으로 가정하고, 각각의 표준 거칠기 모형에서 Barton의 전단강도 기준식을 역해석하여 JCS를 구한 후 적정성을 검토하였다.

절리면압축강도(JCS)의 역산

절리면의 JCS는 일반적으로 절리면에서 측정된 슈미트 햄머 반발값을 이용하여 계산된다. 만약 절리면이 전혀 풍화되지 않고 신선한 경우에는 암석의 일축압축강도를 JCS로 사용하기도 한다. 이 연구에서 사용된 복제 절리면은 신선하므로 석고의 일축압축강도를 JCS로 가정하였다(Table 2). 직접전단시험에서 측정된 전단강도로부터 JCS의 적정성을 검토하기 위하여 Barton의 강도기준식에서 JRC와 $ϕ_{b}$ 를 참값으로 가정한 후, 역해석한 JCS는 다음의 식과 같다.

(4)

J C S = σ_{n} 10^{\frac{1}{J R C} (\tan^{- 1} \frac{τ}{σ_{n}} - ϕ_{b})}

각각의 표준 거칠기 모형에서 수직 응력을 달리하여 5회의 직접전단시험이 실시되었으므로, 각 표준 거칠기 모형에서 5개의 JCS를 역해석하여 계산할 수 있다(Fig. 6). GM-10 석고를 이용하여 복제된 8번 표준 거칠기 모형의 측정 결과에서 역산된 5개의 JCS는 매우 일정한 값을 보이는 반면에, Dental stone을 이용한 4번 표준 거칠기 모형의 측정 결과에서 역산된 5개의 JCS는 20.7~55.1 MPa로 매우 넓은 범위로 분산된 값을 보인다. 전반적으로 4번 표준 거칠기 모형까지는 매우 큰 분산을 보이는 반면에, 5번 표준 거칠기 모형 이후는 비교적 일정한 JCS 값을 보인다. 한 종류의 석고는 하나의 JCS를 가져야 하므로, 각 석고에서 역산된 JCS의 평균을 구하여 붉은 실선으로 표시하였다. GM-10의 평균은 15.4 MPa, Dentalstone은 21.8 MPa, 그리고 Diestone의 평균은 33.0 MPa으로 푸른 점선으로 표시된 석고의 일축압축강도(Table 1 참조)와는 상당한 차이를 보인다. 절리면의 JCS, 특히 신선한 절리면의 JCS는 정확하게 측정될 수 있으며, 역산된 JCS는 측정된 JCS와 큰 차이를 보일 뿐만 아니라 매우 분산된 값으로 보여, JCS의 측정 오류가 Barton의 계산식이 측정값과 차이를 보이는 원인은 아닌 것으로 판단된다.

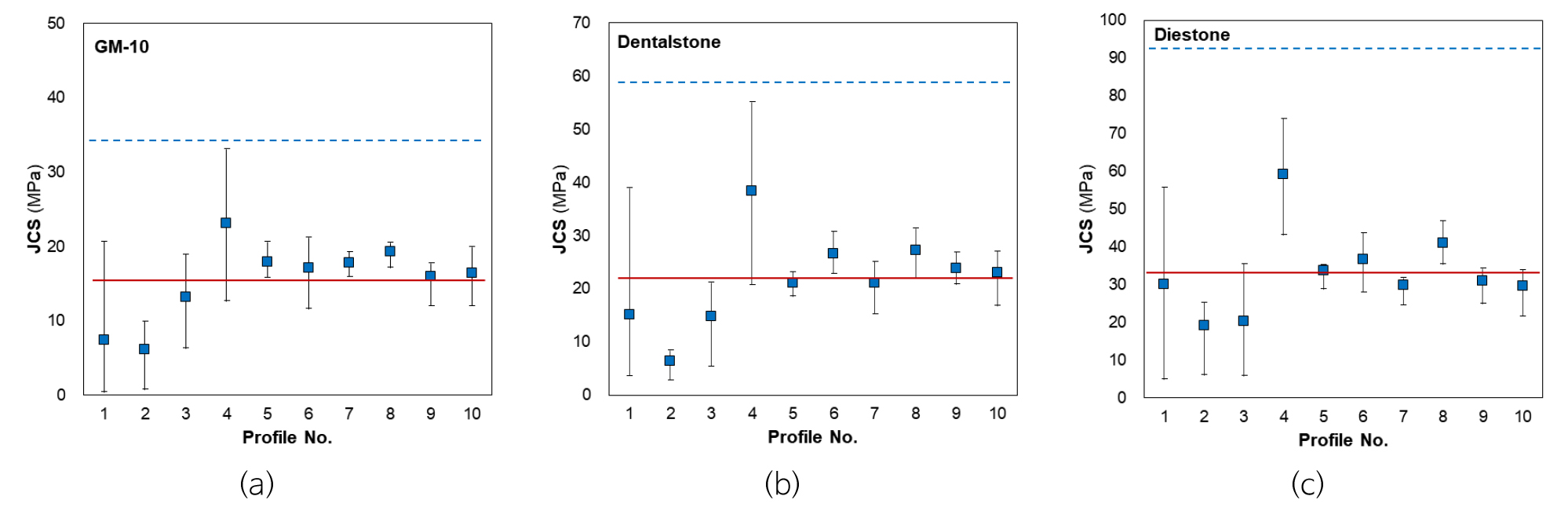
https://static.apub.kr/journalsite/sites/kseg/2021-031-04/N0520310409/images/kseg_31_04_09_F6.jpg

Fig. 6.

Joint compressive strengths (JCS) calculated from direct shear test results for: (a) GM-10; (b) Dental stone; and (c) Diestone. Symbols: ranges of JCS (bars); JCS averages within the same standard roughness profile (■); JCS measured by the uniaxial compressive test (blue dotted lines); and JCS averages calculated from direct shear test results (red solid lines).

기본마찰각( $ϕ_{b}$ )의 역산

$ϕ_{b}$ 는 기울임 시험이나 당김 시험으로 쉽게 구할 수 있는 변수로, ISRM에서는 기울임 시험을 기본마찰각 측정의 표준시험법으로 규정하고 있다. 그러나 기울임 시험에서는 측정값의 분산이 심하고 당김 시험에서 측정된 기본마찰각이 더욱 정확하다는 연구도 있다(Lee et al., 2019). 직접전단시험에서 측정된 전단강도로부터 $ϕ_{b}$ 의 적정성을 검토하기 위하여 JRC와 JCS는 참값으로 가정하고, $ϕ_{b}$ 를 역산하면 다음의 식으로 표현된다.

(5)

ϕ_{b} = \tan^{- 1} \frac{τ}{σ_{n}} - J R C \log \frac{J C S}{σ_{n}}

각각의 표준 거칠기 모형에서 수직 응력을 달리하여 5회의 직접전단시험이 실시되었으므로, 각 표준 거칠기 모형에서 5개의 $ϕ_{b}$ 를 역해석하여 계산할 수 있다(Fig. 7). Dental Stone 석고를 이용한 1번 표준 거칠기 모형에서 역산된 $ϕ_{b}$ 는 36.9~37.3°로 매우 일정한 범위를 보이기도 하지만, Diestone을 이용한 3번 표준 거칠기 모형에서는 30.8~35.4°의 비교적 넓은 범위를 보이기도 한다. 또한 낮은 번호의 표준 거칠기 모형에서 측정된 $ϕ_{b}$ 는 높은 값을 보이다가, 표준 거칠기 번호가 증가함에 따라 점차 낮은 $ϕ_{b}$ 를 나타낸다. 역산된 평균 $ϕ_{b}$ 는 GM-10 석고에서 33.2°, Dental Stone에서 33.2°, Diestone에서는 33.3°를 보여 물질에 따른 기본 마찰각의 차이를 전혀 반영하지 못하고 있으며 측정된 $ϕ_{b}$ 와도 차이를 보여, $ϕ_{b}$ 의 측정 오류가 Barton의 계산식이 측정값과 차이를 보이는 원인은 아닌 것으로 판단된다.

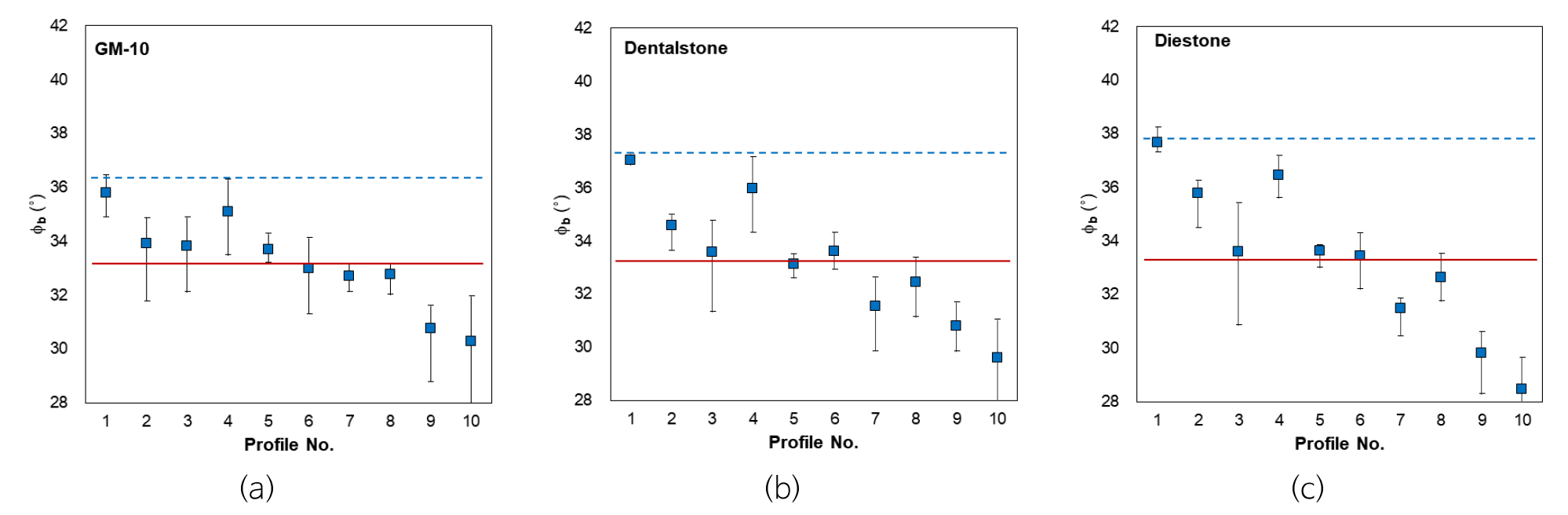
https://static.apub.kr/journalsite/sites/kseg/2021-031-04/N0520310409/images/kseg_31_04_09_F7.jpg

Fig. 7.

Basic friction angles ( $ϕ_{b}$ ) calculated from direct shear test results for: (a) GM-10; (b) Dental stone; and (c) Diestone. Symbols: ranges of (bars); averages of within the same standard roughness profile (■); measured by pull test (blues dotted lines); and averages of from direct shear test results (red solid lines).

절리 거칠기 계수(JRC)의 역산

시험 직접전단시험에서 측정된 전단강도로부터 JCS와 $ϕ_{b}$ 를 참값으로 가정하고 JRC를 역산하였다. JRC는 다음의 식에서 계산된다.

(6)

J R C = \frac{\tan^{- 1} \frac{τ}{σ_{n}} - ϕ_{b}}{\log \frac{J C S}{σ_{n}}}

각각의 표준 거칠기 모형에서 측정된 수직응력과 전단응력의 자료로부터 역산된 JRC는 Fig. 8과 같다. 각 표준거칠기 모형에서 측정된 5개의 JRC는 6~9번 표준거칠기 모형에서 비교적 넓은 범위를 보이기도 하지만 전반적으로 일정한 값을 나타내고 있다. 역산된 JRC는 Barton and Choubey(1977)가 제시한 JRC보다 낮은 값을 보이지만 표준 거칠기 번호가 증가하면 JRC도 증가하는 형태를 보인다. 각 표준 거칠기 단면에서 역산된 5개의 JRC 값은 JCS와 $ϕ_{b}$ 와는 다르게 매우 좁은 범위에 분포하고 있으며 거칠기가 증가하면 JRC 값도 증가하므로, Barton and Choubey(1977)가 제시한 표준 거칠기 단면의 JRC 값이 정확하지 않기 때문에 추정된 전단강도와 측정된 전단강도의 차이가 발생하는 것으로 판단된다.

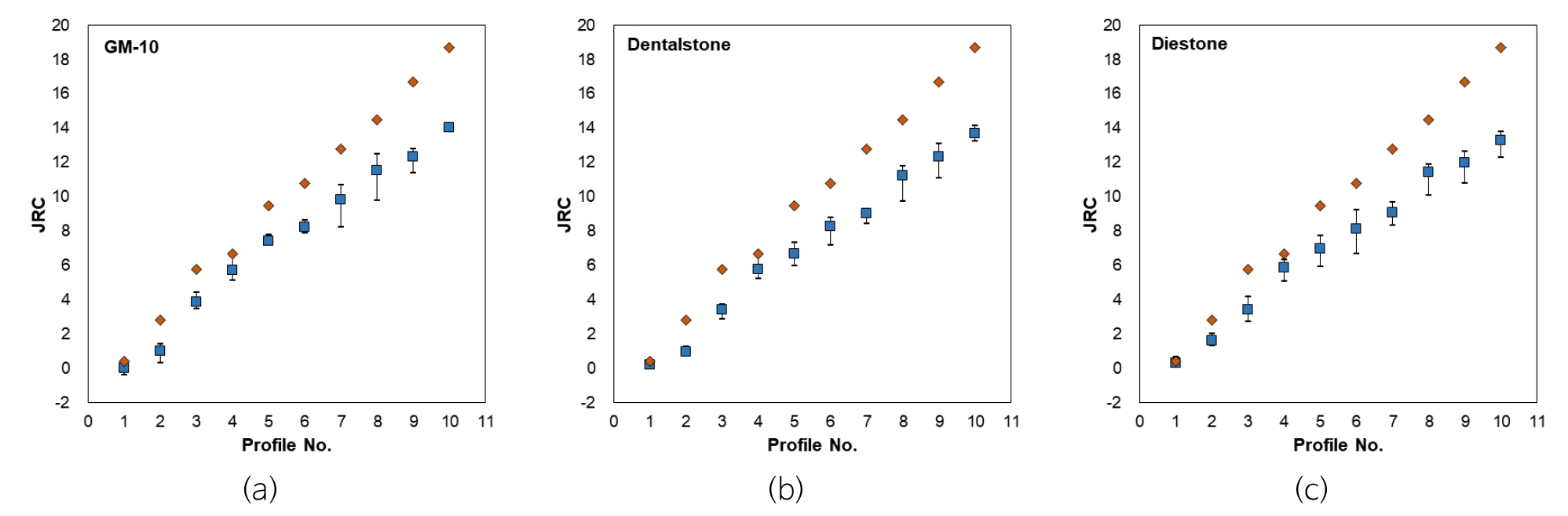
https://static.apub.kr/journalsite/sites/kseg/2021-031-04/N0520310409/images/kseg_31_04_09_F8.jpg

Fig. 8.

Joint roughness coefficients (JRC) calculated from direct shear test results for: (a) GM-10; (b) Dental stone; and (c) Diestone. Symbols: JRC ranges (bars); averages of JRC within the same standard roughness profile (■); and JRC values suggested by Barton and Choubey (1977; ◆).

표준 거칠기 단면의 정확한 거칠기 계수 결정

각각의 표준 거칠기 단면에서 역산된 JRC의 평균값은 Table 5와 같다. 역산된 JRC는 0.1에서 14.0까지 분포하고 있으며, 각각의 표준 거칠기 단면에서는 석고의 종류에 따라 0.8 이내의 오차를 보인다. 하나의 표준 거칠기 단면은 석고의 종류에 관계없이 하나의 JRC 값을 가져야 하므로, 세 종류의 석고에서 역산된 JRC의 평균값을 구하여 이 표준 거칠기 단면의 JRC 값으로 결정하였고, 이를 수정된 JRC라는 뜻으로 JRC_m으로 명명하였다. JRC_m은 0.2에서 13.7의 범위를 보이고 있으며, 모든 표준 거칠기 단면에서 Barton and Choubey(1977)가 제안한 JRC보다 낮은 값을 가진다. 이러한 낮은 JRC는 Hsiung et al.(1993)과 Jang et al.(2010)에서도 보고된 바 있다.

Table 5.

JRC values back calculated from the direct shear tests of replica joint models

Profile No.		1	2	3	4	5	6	7	8	9	10
JRC	GM-10	0.1	1.0	3.9	5.7	7.4	8.2	9.8	11.5	12.3	14.0
	Dental Stone	0.2	1.0	3.4	5.8	6.7	8.3	9.0	11.2	12.4	13.7
	Diestone	0.3	1.6	3.4	5.9	7.0	8.1	9.1	11.4	12.0	13.3
JRC_m		0.2	1.2	3.6	5.8	7.0	8.2	9.3	11.4	12.2	13.7
JRC (Barton and Choubey, 1977)		0.4	2.8	5.8	6.7	9.5	10.8	12.8	14.5	16.7	18.7

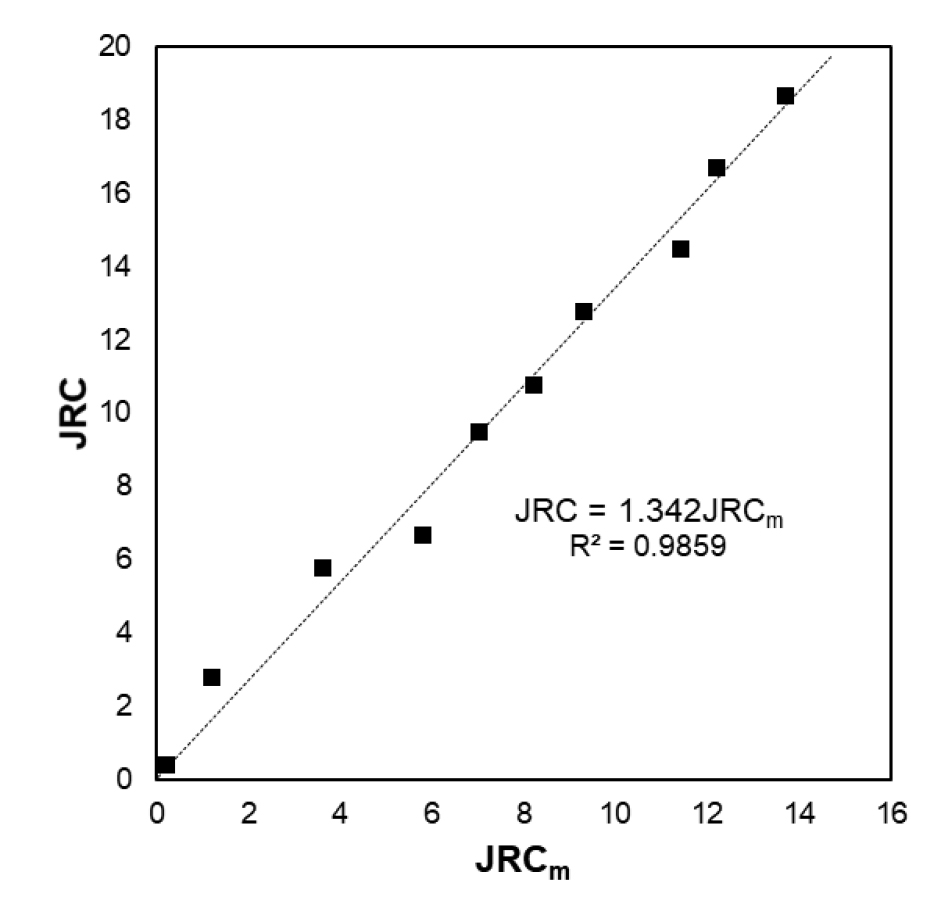
Fig. 9는 Barton and Choubey(1977)가 제안한 JRC와 JRC_m의 관계를 보여준다. JRC는 JRC_m과 비교적 양호한 직선의 관계를 보이고 있으므로, 직선의 식으로 회귀분석을 실시하였다. JRC는 JRC_m과 결정계수( $R^{2}$ )가 0.986인 매우 좋은 직선의 상관관계를 보이며, 두 변수의 상관관계는 식 (7)과 같다.

(7)

J R C = 1.342 J R C_{m} or J R C_{m} = 0.743 J R C

https://static.apub.kr/journalsite/sites/kseg/2021-031-04/N0520310409/images/kseg_31_04_09_F9.jpg

Fig. 9.

Relationship between JRC and JRC_m.

통계적 변수 Z₂와 역산된 JRC_m의 상관관계

절리의 거칠기를 표준 거칠기 단면과 육안으로 비교하여 JRC를 결정하는 방법은 측정 오차가 발생하기 때문에, 많은 연구자들이 수치화된 절리 단면과 표준 거칠기 단면에서 측정된 통계적 변수(statistical parameter)와 JRC의 상관관계를 사용하여 JRC를 결정하고자 노력하였다(Wu and Ali, 1978; Tse and Cruden, 1979; Lee et al., 1990; Wakabayashi and Fukushige, 1995; Jang et al. 2005, 2014). 통계적 변수에는 거칠기 높이에 대한 제곱평균자승근(RMS), 거칠기의 기울기에 대한 제곱평균자승근( $Z_{2}$ ), 구조함수(SF), 거칠기의 미소-평균각( $A_{i}$ ) 등이 있으나, 이러한 통계적 변수 중에서 $Z_{2}$ 와 JRC의 상관관계가 가장 많이 연구되었고, 현재도 사용되고 있다(Lee et al., 1990; Wakabayashi and Fukushige, 1995; Jang et al., 2005, 2014). 그러나 이러한 상관관계는 Barton and Choubey(1977)가 표준 거칠기 단면에 부여한 JRC 값에 근거하고 있으므로, 표준 거칠기에 부여된 JRC 값이 달라지면 상관관계 또한 바뀌어야 한다. 이 연구에서는 표준 거칠기 단면의 $Z_{2}$ 와 새로이 결정된 표준 거칠기 단면의 JRC_m의 상관관계를 결정하였다.

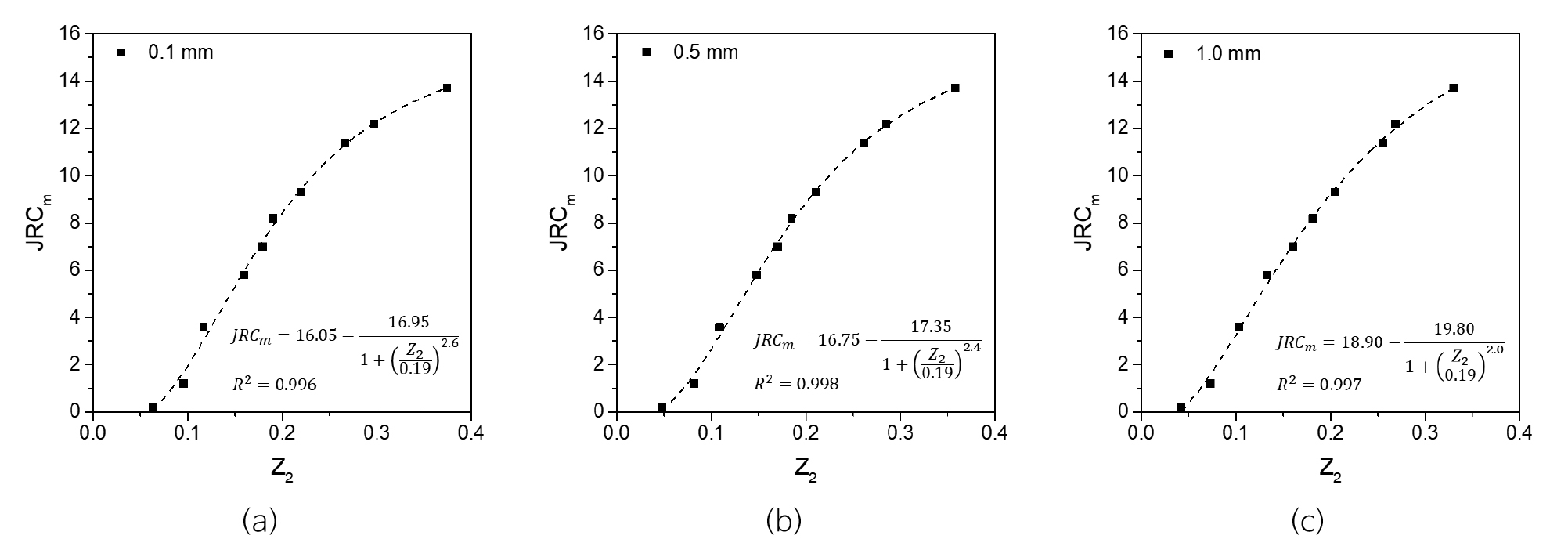
$Z_{2}$ 는 JRC와 상당히 좋은 상관관계를 갖는 것으로 알려져 있으나 절리 단면의 수치화 과정에서 사용된 측정 간격(sampling interval, SI)에 영향을 받는 문제점이 있다(Miller et al., 1990; Yu and Vayssade, 1991; Jang et al., 2014). 그러므로 0.1 mm, 0.5 mm, 1.0 mm의 3종류의 측정 간격에 대하여 $Z_{2}$ 와 JRC_m의 상관관계를 결정하였다(Fig. 10). 모든 측정 간격에서 $Z_{2}$ 가 증가할수록 JRC_m도 증가하는 곡선의 관계를 보이며, 낮은 $Z_{2}$ 에서는 위로 오목한 형태를 보이는 반면에, 높은 $Z_{2}$ 에서는 위로 볼록한 S자 곡선의 형태를 보인다. 이 곡선에 가장 최적인 곡선을 회귀분석을 하면 로지스틱(logistic) 함수인 식 (8)에서 식 (10)으로 나타나며, 각 회귀식의 결정계수 $R^{2}$ 는 0.996 이상인 매우 좋은 상관관계를 보인다.

(8)

J R C_{m} = 16.05 - \frac{16.95}{1 + {(\frac{Z_{2}}{0.19})}^{2.6}} R^{2} = 0.996, S I = 0.1 m m

(9)

J R C_{m} = 16.75 - \frac{17.35}{1 + {(\frac{Z_{2}}{0.19})}^{2.4}} R^{2} = 0.998, S I = 0.5 m m

(10)

J R C_{m} = 18.90 - \frac{19.80}{1 + {(\frac{Z_{2}}{0.19})}^{2.0}} R^{2} = 0.997, S I = 1.0 m m

https://static.apub.kr/journalsite/sites/kseg/2021-031-04/N0520310409/images/kseg_31_04_09_F10.jpg

Fig. 10.

Relationships between the JRC_m of the standard roughness profiles and for sampling intervals of (a) 0.1 mm, (b) 0.5 mm, and (c) 1.0 mm.

Barton의 전단강도 기준식의 수정 및 검증

Barton의 전단강도 기준식과 10개의 표준 거칠기 단면의 JRC 값은 1970년대에 제안된 이후 많은 엔지니어들에게 사용되어왔다. 그러나 표준 거칠기 단면을 3차원으로 확장하여 모든 단면의 JRC가 일정한 3차원 절리 모델에 직접전단시험을 실시하여 측정한 전단강도는 Barton의 전단강도 기준식에서 추정된 전단강도와 차이를 보였다. 직접전단시험에서 측정된 전단강도로부터 Barton의 전단강도 기준식에 사용된 세 가지의 변수, JCS, $ϕ_{b}$ 및 JRC를 역산하였고, 표준거칠기 단면에 부여된 JRC 값의 문제로 인하여 추정된 전단강도와 측정된 전단강도가 차이를 보이는 것으로 판명되어, 새로운 JRC_m을 제안하였다. 이에 따라 Barton의 전단강도 기준식이 수정될 필요가 대두되었고, 표준거칠기 단면에 새롭게 부여된 거칠기 계수, JRC_m을 사용한 전단강도 기준식은 식 (11)과 같다. 만약 Barton and Choubey(1977)가 부여한 표준거칠기 단면의 JRC 값을 사용하고자 한다면 절리면 전단강도는 식 (12)와 같이 수정되어야 한다.

(11)

τ = σ \tan [J R C_{m} \log \frac{J C S}{σ} + ϕ_{b}]

(12)

τ = σ \tan [0.743 J R C \log \frac{J C S}{σ} + ϕ_{b}]

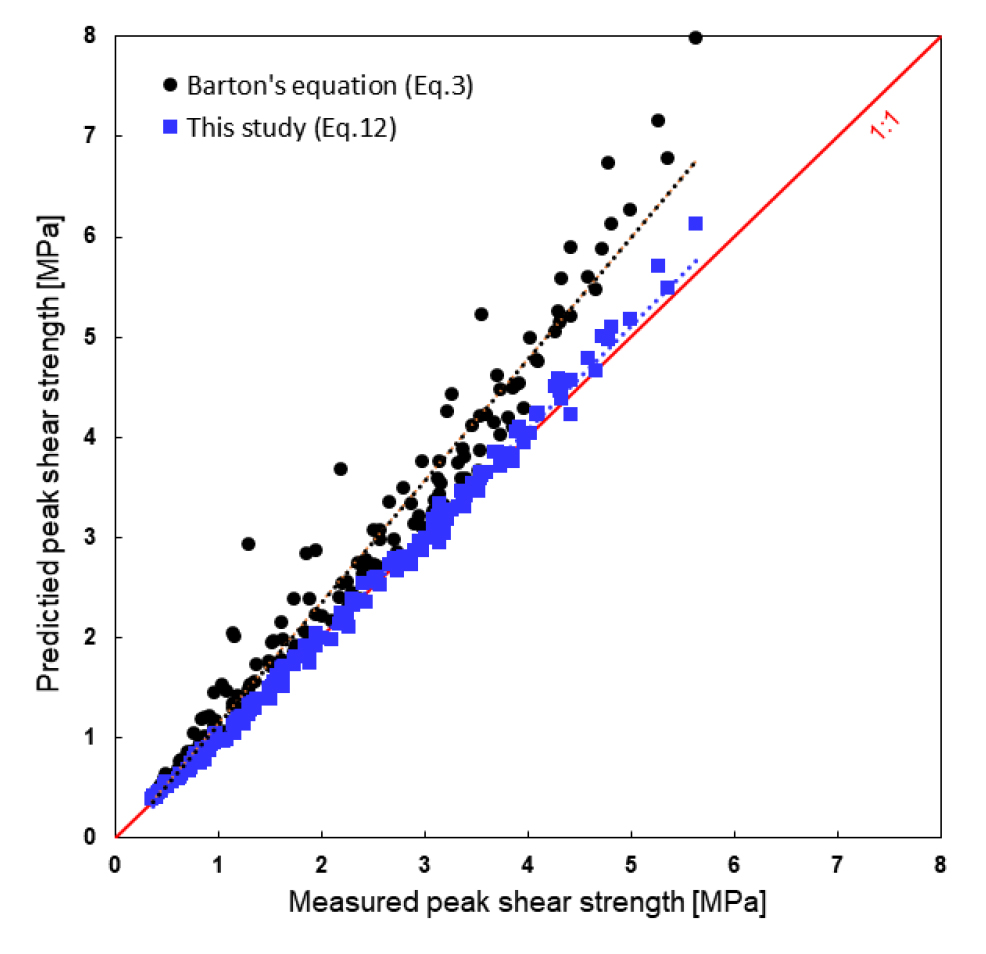
측정된 절리면 전단강도를 Barton and Choubey(1977)가 부여한 표준거칠기 단면의 JRC 값을 사용하여 추정한 전단강도와 새롭게 수정된 표준거칠기 단면의 JRC_m 값을 사용하여 추정한 전단강도를 비교하였다(Fig. 11). Barton and Choubey(1977)가 부여한 표준거칠기 단면의 JRC 값을 사용하여 추정된 전단강도는 측정된 전단강도보다 큰 값을 보여 그림의 좌측 상부에 분포하고 있으며, 결정계수는 0.969로 비교적 좋은 편이나 약간의 분산도 보이고 있다. 반면에 JRC_m을 사용하여 추정된 전단강도는 측정값이 아주 일치하여 거의 모든 점들이 대각선상에 분포하고 있으며, 결정계수 또한 0.996로 아주 좋은 상관관계를 보여준다.

https://static.apub.kr/journalsite/sites/kseg/2021-031-04/N0520310409/images/kseg_31_04_09_F11.jpg

Fig. 11.

Relationship between predicted peak shear strengths using JRC and JRC_m, and measured peak shear strengths.

요약 및 결론

표준 거칠기 단면을 3차원으로 확장하여 만든 복제 절리시료에 직접전단시험을 실시하여 측정한 전단강도는 Barton의 전단강도 기준식에서 추정된 전단강도와 차이를 보였다. 1번과 4번 표준 거칠기 단면에서 측정된 전단강도는 Barton의 강도기준과 비교적 일치하지만, 그 외의 8개 표준 거칠기 단면에서 측정된 전단강도는 Barton의 강도기준에서 계산된 응력보다 낮고, JRC가 클수록 차이가 더 크게 나타났다. 이는 Barton의 전단강도 기준식 내에 있는 변수인 JRC, JCS 그리고 $ϕ_{b}$ 중의 일부 혹은 모두에서 문제가 있을 수도 있다는 것을 보여준다. 따라서 전단강도 기준식 내의 세 변수의 적정성과 오차를 역해석을 통하여 분석하였다. 전단시험에 대한 역해석으로 계산된 JCS는 일축압축시험으로 구한 JCS와 큰 차이를 보일 뿐만 아니라 같은 물질에서도 매우 분산된 형태를 보였으며, 역해석으로 계산된 $ϕ_{b}$ 역시 같은 물질에서도 분산된 결과가 나타나고 실제 측정된 $ϕ_{b}$ 와도 차이가 있어 JCS와 $ϕ_{b}$ 의 측정 오류가 Barton의 계산식이 측정값과 차이를 보이는 원인은 아닌 것으로 판단된다(Figs. 5, 6). 역해석으로 계산된 JRC는 JCS와 $ϕ_{b}$ 와는 다르게 값이 분산되어 있지 않고 거칠기가 증가할수록 JRC 값도 증가하는 경향을 보인다. 그러나 역산된 JRC는 전반적으로 Barton and Choubey(1977)가 제시한 JRC보다 낮은 값을 보이며, 거칠기가 클수록 더 큰 차이를 보였다(Fig. 7). 이는 Barton and Choubey(1977)가 제시한 표준 거칠기 단면의 JRC 값이 실제 JRC와 차이가 있다는 것을 보여주며, 이러한 오류가 Barton의 계산식이 측정값과 차이를 보이는 원인으로 작용했을 것으로 판단된다. 이 연구에서는 역해석으로 구한 JRC를 수정된 JRC라는 뜻의 JRC_m으로 정의하고 JRC_m과 Barton and Choubey(1977)가 제시한 JRC와의 회기분석을 실시하여 상관성이 매우 높은 직선의 관계식(식 (7))을 도출하였으며 거칠기 정량화 기법으로 가장 많이 사용되는 통계적 변수인 Z₂로부터 JRC_m을 결정할 수 있는 관계식(식 (8), (9), (10))도 도출하였다. 수정된 거칠기 계수인 JRC_m이 새롭게 제시됨에 Barton and Choubey(1977)의 전단강도 기준식은 JRC를 JRC_m으로 대체한 식 (11)로 수정될 수 있다. 만약 Barton and Choubey(1977)가 부여한 기존의 JRC 값을 그대로 사용하고자 한다면 절리면 전단강도 기준식은 식 (12)와 같이 수정되어야 한다. 수정된 전단강도 기준식인 식 (11) 또는 식 (12)를 사용하여 계산된 전단강도는 직접전단시험에서 측정된 최대 전단강도와 매우 잘 일치하는 것으로 분석되었다. 따라서 이 연구에서 제시한 수정된 전단강도 기준식을 사용하여 전단강도를 예측할 경우 기존의 Barton의 전단강도기준이 갖고 있던 오차의 문제를 보완할 수 있을 것으로 판단된다. 그러나 이러한 결과는 인공물질인 석고로 제작된 복제절리를 이용한 실험적, 경험적 연구로부터 도출된 것이므로 절리면 전단강도기준으로 충분한 신뢰성을 얻기 위해서는 실제 암석 절리를 이용한 추가 연구가 필요할 것으로 판단된다.

Acknowledgements

이 논문은 교육부의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업(2018R1A2B6004886, 2019R1A6A1A03033167)과 행정안전부의 지진방재분야 전문인력 양성사업의 지원을 받았음.

References

Alejano, L.R., Muralha, J., Ulusay, R., Li, C.C., Pérez-Rey, I., Karakul, H., Chryssanthakis, P., Aydan, Ö., 2018, ISRM suggested method for determining the basic friction angle of planar rock surfaces by means of tilt tests, Rock Mechanics and Rock Engineering, 51, 3853-3859. 10.1007/s00603-018-1627-6

Barton, N., 1973, Review of a new shear-strength criterion for rock joints, Engineering Geology, 7, 287-332. 10.1016/0013-7952(73)90013-6

Barton, N., Choubey, V., 1977, The shear strength of rock joints in theory and practice, Rock Mechanics, 10, 1-54. 10.1007/BF01261801

Belem, T., Homana-Etienne, F., Souley, M., 2000, Quantitative parameters for rock joint surface roughness, Rock Mechanics and Rock Engineering, 33, 217-242. 10.1007/s006030070001

Byerlee, J.D., 1967, Frictional characteristics of granite under high confining pressure, Journal of Geophysical Research, 72, 3639-3648. 10.1029/JZ072i014p03639

Cruden, D.M., Hu, X.Q., 1988, Basic friction angles of carbonate rocks from Kananaskis country, Canada, Bulletin of Engineering Geology and the Environment, 38, 55-59. 10.1007/BF02590448

Fan, W., Cao, P., 2020, A new 3D JRC calculation method of rock joint based on laboratory-scale morphology testing and its application in shear strength analysis, Bulletin of Engineering Geology and the Environment, 79, 345-354. 10.1007/s10064-019-01569-0

González, J., González-Pastoriza, N., Castro, U., Alejano, L.R., Muralha, J., 2014, Considerations on the laboratory estimate of the basic friction angle of rock joints, In: Alejano, R., Perucho, A., Olalla, C., Jimenez, R. (Eds.), Rock Engineering and Rock Mechanics: Structures in and on Rock Masses (EUROCK 2014), ISRM European Regional Symposium, Vigo, 199-204. 10.1201/b16955-3124826208PMC4018244

Grasselli, G., Egger, P., 2003, Constitutive law for the shear strength of rock joints based on three-dimensional surface parameters, International Journal of Rock Mechanics and Mining Sciences, 40, 25-40. 10.1016/S1365-1609(02)00101-6

Grasselli, G., Wirth, J., Egger, P., 2002, Quantitative three-dimensional description of a rough surface and parameter evolution with shearing, International Journal of Rock Mechanics and Mining Sciences, 39, 789-800. 10.1016/S1365-1609(02)00070-9

Hsiung, S.M., Ghosh, A., Ahola, M.P., Chowdhury, A.H., 1993, Assessment of conventional methodologies for joint roughness coefficient determination, International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 30, 825-829. 10.1016/0148-9062(93)90030-H

Jang, B.A., Kim, T.H., Jang, H.S., 2010, Characterization of the three dimensional roughness of rock joints and proposal of a modified shear strength criterion, The Journal of Engineering Geology, 20, 319-327 (in Korean with English abstract).

Jang, H.S., Jang, B.A., Kim, Y., 2005, Estimation of joint roughness coefficient (JRC) using modified divider method, The Journal of Engineering Geology, 15, 269-280 (in Korean with English abstract).

Jang, H.S., Kang, S.S., Jang, B.A., 2014, Determination of joint roughness coefficients using roughness parameters, Rock Mechanics and Rock Engineering, 47, 2061-2073. 10.1007/s00603-013-0535-z

Kulatilake, P.H.S.W., Shou, G., Huang, T.H., Morgan, R.M., 1995, New peak shear strength criteria for anisotropic rock joints, International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 32, 673-697. 10.1016/0148-9062(95)00022-9

Ladanyi, B., Archambault, G., 1970, Simulation of shear behaviour of a jointed rock mass, In: Somerton, W.H. (Ed.), Proceedings of the 11th U.S. Symposium on Rock Mechanics (USRMS), Berkeley, 105-125.

Lane, K.S., Heck, W.J., 1964, Triaxial testing for strength of rock joints, In: Spokes, E.M., Christiansen, C.R. (Eds.), Proceedings of the 6th U.S. Symposium on Rock Mechanics (USRMS), Rolla, 98-108.

Lee, K.H., Jang, H.S., Jang, B.A., 2019, Experimental study for optimal method in measuring the basic friction angle of rock, The Journal of Engineering Geology, 22, 565-578 (in Korean with English abstract).

Lee, Y.H., Carr, J.R., Barr, D.J., Hass, C.J., 1990, The fractal dimension as a measure of the roughness of rock discontinuity profiles, International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 27, 453-464. 10.1016/0148-9062(90)90998-H

Liu, X.G., Zhu, W.C., Yu, Q.L., Chen, S.J., Li, R.F., 2017, Estimation of the joint roughness coefficient of rock joints by consideration of two-order asperity and its application in double-joint shear tests, Engineering Geology, 220, 243-255. 10.1016/j.enggeo.2017.02.012

Maerz, N.H., Franklin, J.A., Bennett, C.P., 1990, Joint roughness measurement using shadow profilometry, International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 27, 329-343. 10.1016/0148-9062(90)92708-M

Miller, S.M., McWilliams, P.C., Kerkering, J.C., 1990, Ambiguities in estimating fractal dimensions of rock fracture surfaces, Proceedings of the 31st U.S. Symposium on Rock Mechanics (USRMS), Colden, 147-478.

Park, J.W., Song, J.J., 2013, Numerical method for the determination of contact areas of a rock joint under normal and shear loads, International Journal of Rock Mechanics and Mining Sciences, 58, 8-22. 10.1016/j.ijrmms.2012.10.001

Patton, F.D., 1966, Multiple modes of shear failure in rock and related material, Ph.D. Thesis, University of Illinois, 282p.

Stimpson, B., 1981, A suggested technique for determining the basic friction angle of rock surfaces using core, International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 18, 63-65. 10.1016/0148-9062(81)90266-7

Tse, R., Cruden, D.M., 1979, Estimating joint roughness coefficients, International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 16, 303-307. 10.1016/0148-9062(79)90241-9

Wakabayashi, N., Fukushige, I., 1995, Experimental study on the relation between fractal dimension and shear strength, In: Myer, L.R., Cook, N.G.W., Goodman, R.E., Tsang, C.F. (Eds.), Fractured and jointed rock masses, Balkema, Rotterdam, 125-131.

Wang, C., Wang, L., Karakus, M., 2019, A new spectral analysis method for determining the joint roughness coefficient of rock joints, International Journal of Rock Mechanics and Mining Sciences, 113, 72-82. 10.1016/j.ijrmms.2018.11.009

Wang, G., Zhang, X., Jiang, Y., Wu, X., Wang, S., 2016, Rate-dependent mechanical behavior of rough rock joints, InterJournal of Rock Mechanics and Mining Sciences, 83, 231-240. 10.1016/j.ijrmms.2015.10.013

Wang, G., Zhang, Y., Jiang, Y., Liu, P., Guo, Y., Liu, J., Wang, S., 2018, Shear behaviour and acoustic emission characteristics of bolted rock joints with different roughnesses, Rock Mechanics and Rock Engineering, 51, 1885-1906. 10.1007/s00603-018-1438-9

Wu, T.H., Ali, E.M., 1978, Statistical representation of joint roughness, International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 15, 259-262. 10.1016/0148-9062(78)90958-0

Yang, Z.Y., Chiang, D.Y., 2000, An experimental study on the progressive shear behavior of rock joints with tooth-shaped asperities, International Journal of Rock Mechanics and Mining Sciences, 37, 1247-1259. 10.1016/S1365-1609(00)00055-1

Yu, X., Vayssade, B., 1991, Joint profiles and their roughness parameters, International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 28, 333-336. 10.1016/0148-9062(91)90598-G

The Journal of Engineering Geology ISSN:1226-5268(Print) 2287-7169(Online) 지질공학

Preview

New Joint Roughness Coefficient and Shear Strength Criterion Based on Experimental Verification of Standard Roughness Profile

ABSTRACT

MAIN

(1)

(2)

(3)

Table 1.

Standard roughness profiles suggested by Barton and Choubey (1977). The numbers within parentheses are the exact JRC values

Fig. 1.

(a) Three-dimensional profile of a joint showing different roughness according to the scanning lines. (b) Joint roughness coefficients (JRC) measured along 30 different scanning lines (Jang et al., 2010).

Fig. 2.

(a) Three-dimensional joint model produced by digitized values of the eighth standard roughness profile. (b) Joint model produced by a 3D printer from the digitized 3D joint model.

Table 2.

JRC values suggested by Barton and Choubey (1977) and Jang et al. (2014), and those measured from joint models produced by 3D printer

Table 3.

Physical and mechanical properties of the plasters

Table 4.

Basic friction angles determined by the tilt test and the pull test

Fig. 3.

Direct shear test apparatus.

Fig. 4.

Plot of shear stress versus shear displacement measured from replica joints of the fourth standard roughness profile using GM-10 plaster.

Fig. 5.

Shear stresses measured by direct shear tests for GM-10 (◆), Dental Stone (●), and Diestone (■). Solid lines represent Barton’s failure criterion (Barton, 1973) for three types of plaster: GM-10 (green); Dental Stone (red); and Diestone (blue).

(4)

Fig. 6.

(5)

Fig. 7.

(6)

Fig. 8.

Joint roughness coefficients (JRC) calculated from direct shear test results for: (a) GM-10; (b) Dental stone; and (c) Diestone. Symbols: JRC ranges (bars); averages of JRC within the same standard roughness profile (■); and JRC values suggested by Barton and Choubey (1977; ◆).

Table 5.

JRC values back calculated from the direct shear tests of replica joint models

(7)

Fig. 9.

Relationship between JRC and JRCm.

(8)

(9)

(10)

Fig. 10.

Relationships between the JRCm of the standard roughness profiles and for sampling intervals of (a) 0.1 mm, (b) 0.5 mm, and (c) 1.0 mm.

(11)

(12)

Fig. 11.

Relationship between predicted peak shear strengths using JRC and JRCm, and measured peak shear strengths.

Acknowledgements

References

Relationship between JRC and JRC_m.

Relationships between the JRC_m of the standard roughness profiles and for sampling intervals of (a) 0.1 mm, (b) 0.5 mm, and (c) 1.0 mm.

Relationship between predicted peak shear strengths using JRC and JRC_m, and measured peak shear strengths.