서 론
연구의 배경 및 목적
선행연구 분석
회전관입말뚝의 이론적 배경
회전관입말뚝의 지지력 이론
회전관입말뚝의 개선
현장실험
현장실험 개요
대상지반의 조건
현장시험시공
재하시험방법
현장실험 결과
압축재하시험 결과
인발재하시험 결과
결 론
서 론
연구의 배경 및 목적
회전관입말뚝(Helical pile)은 중공형 축(Shaft)에 한 개 이상의 나선형 원판(Helix plate)을 부착한 후 지반에 회전으로 관입시켜 지지력을 발현하게 하는 비배토 말뚝기초이다. 회전관입말뚝의 장점은 목표 심도까지 회전관입을 시키는 회전관입기(Torque machine)에 의해 저소음 ‧ 저진동으로 시공이 가능한 비교적 소형의 장비로서 장비의 조작이 간단하며, 상업적으로 사용되고 있는 건물 또는 유적지, 도서지역과 같은 대형장비가 들어갈 수 없는 지역 등과 같이 시공부지가 한정된 곳에서 시공이 가능하다는 장점이 있다. 또한 회전관입말뚝은 중공형 축에 큰 직경을 갖는 나선형 원판이 부착되어 각각의 나선형 원판이 선단지지력을 발휘할 수 있으므로(Livneh and Naggar, 2008) 기존의 강관말뚝에 비해 지지력 측면, 경제적 측면에서 큰 이점을 갖는다.
이러한 회전관입말뚝은 급속한 산업화와 경제발전으로 인한 가속화로 인해 협소한 공간에서의 시공, 대형장비 진입이 불가한 도서지역에서 소형장비의 운영을 통한 소구경 말뚝을 적용한 합리적인 시공 및 설계가 가능하다. 그러므로 소형장비를 사용하여 소구경 말뚝 형태의 기초보강방법의 적용이 주로 검토되어 지고, 기성제품을 사용하여 시공 중에 품질관리 및 시공 완료 후 성능평가 방법 또한 그라우팅 공법 등을 이용한 지반보강 공법에 비해 용이하다는 장점이 있다(Lee, 2017).
이와 같은 다양한 장점으로 인하여 미국 및 유럽에서는 회전관입말뚝을 오래전부터 다양한 현장에서 이용해왔다. 하지만 국내에는 회전관입말뚝의 장점이 충분히 소개되지 않았고, 다만 회전관입말뚝과 형상이 유사한 스크류 앵커 파일에 관한 연구(Yoo, 2012), 현장 시공된 회전관입말뚝의 지지력에 관하여 기존의 지지력 예측 공식과 비교분석한 사례 등이 있다.
회전관입말뚝은 대부분 정형화된 형상을 가지고 있으며, 중공형의 직경, 나선형 직경에 따른 지지력에 대한 연구가 진행되어 왔다. 그러나 대부분 시공방식을 단순화하기 위해 볼트(Bolt) 및 현장 용접방식을 취하고 있으나, 말뚝의 시공 시 수직도의 불량, 회전관입 중 볼트 파손에 따른 작업자의 안전 문제, 현장 용접에 의한 용접사 인건비와 용접공종 추가에 의한 공사기간의 증가, 별도의 용접부 품질관리가 필요한 문제점 등이 대두되고 있으므로 이를 극복할 수 있는 새로운 방식의 이음부의 적용이 필요하다고 판단되었다.
현재 회전관입말뚝의 지지력 예측은 기존 Terzaghi(1943)의 산정식이나 Meyerhof(1951)의 산정식을 사용하고 있다. 하지만 회전관입말뚝은 기존 말뚝과는 상이한 형상이므로 기존의 산정식에 대하여 높은 신뢰도를 기대할 수 없으며, 기존 산정식을 그대로 사용하기 위해서는 국내 지반에서 시공된 회전관입말뚝의 지지력에 대한 검토가 필요하다(Lee, 2014). 또한 미국에서 개발된 회전관입말뚝의 공법이 국내 적용성에 대한 검토 없이 무분별하게 적용되어 왔고, 미국 산정식에 근거한 설계로 국내 지반의 특성에 대한 반영이 미흡한 실정이므로 지반조건과 재하시험결과 등을 반영한 체계적인 연구로 국내 지반 특성을 고려한 설계법이 필요한 실정이다.
따라서 본 연구에서는 중공형 축의 모형을 육각형 이음부로 압연하여 압축재하 시 별도의 용접이나 볼트가 필요 없는 끼워 맞춤식으로 개선하였으며, 그에 따른 국내 지반에 적용하기 위해 가장 일반적인 지반(퇴적토, 풍화토, 풍화암, 연암)으로 구성된 현장 Site 2곳을 선택하여 현장시험시공 및 재하시험을 수행하였다. 현장재하시험 시 압축재하시험 및 인발재하시험의 결과를 통해 현장적용성을 검토하고자 하였다.
선행연구 분석
말뚝들의 구경이 작고 여러 가지 장점을 갖추었다는 의미에서 강소말뚝으로 칭하고 있으며, 강소말뚝 중 회전력을 통하여 비배토로 지반에 관입하여 지지력을 나타내는 말뚝을 일명 스크류말뚝(Screw pile), 회전관입말뚝 등으로도 불리고 있다.
Lee et al.(2010)은 마이크로파일은 연암층 이상을 지지층으로 설계되어야 하므로 말뚝의 길이가 길어지는 단점이 있어 회전관입말뚝이 좋은 대안이 될 수 있다고 발표하였고, Kim(2012)은 소구경파일의 실내외실험을 통하여 나선형 원판의 최적제원 결정과 시공성 향상, 지지력 증대효과를 검증한 바 있다.
Yoo(2012), Cho et al.(2013), Kim and Yoo(2013), Yoo and Kim(2014)은 스크류 앵커 말뚝의 인발저항 특성을 연구하였는데 나선형 원판(Helix)의 직경 및 간격(Pitch) 등 기하학적 특성을 달리하여 실내실험을 수행하였다. 실험결과, 일정한 나선형 원판 간격의 조건에서 나선형 원판 크기가 증가하면 인발저항력은 증가하다 일정 크기 이상에서 일정해지는 것을 확인하였다.
Lee et al.(2014), Lee and Lee(2016), Seo(2016)는 현장 재하시험 결과와 Individual bearing method, Cylindrical shear method, Torque correlation method의 지지력을 비교하였다. 실험결과, Torque correlation method가 가장 상관성이 높음을 확인하였다.
Park and Kim(2015)은 회전관입말뚝이 경질(암반)의 지반에 안착되었을 경우 1,000.0 kN의 지지력을 확보할 수 있을 것으로 평가하였으며, 회전관입말뚝의 요구 지지력을 최소의 자재비용과 최적의 회전관입말뚝 형상으로 하모니서치 알고리즘(Harmony search algorithm)을 적용하여 최적화된 설계법을 나타냈다.
국외에서의 회전관입말뚝에 대한 연구는 주로 앵커로 활용하기 위한 인발력 평가를 중심으로 이루어져 왔다. Mitsch and Clemence(1985)는 극한하중하의 회전관입 앵커 주위의 지반 거동에 관하여 연구하고 앵커의 인발력을 산정하는 근사식을 산정하였다. 또한 회전관입 앵커의 설치 또는 인발 중 토압의 변화를 측정하기 위하여 Clemence and Pepe(1984)는 여러 가지 실내 모형실험을 하였으며, 이를 근거로 하여 앵커의 설치 동안에 흙의 분산 때문에 토압의 감소현상이 발생한다는 사실을 밝혔다.
Mooney et al.(1985)은 각각 사질토와 점성토에 근입되어 있는 단일 및 다중 회전관입 앵커의 인발저항 특성에 대한 연구를 수행하고 그 결과를 토대로 회전관입 앵커의 관입깊이, 스크류 날개의 직경, 그리고 지반 조건에 따른 인발저항력을 산정할 수 있는 경험식을 발표한 바 있다.
Narasimha et al.(1991)은 회전관입 앵커의 인발력을 결정하는 영향인자가 인발력에 미치는 영향에 대한 연구를 실시하였으며, Merifield and Smith(2010)는 점토에 설치되는 회전관입 앵커의 극한 인발저항에 관한 수치해석적 연구를 수행하고 그 결과를 토대로 극한 인발저항과 회전관입 말뚝의 설치 제원과의 관계를 고찰하였다.
나선형 회전관입말뚝의 지지력 거동에 대해서는 Narasimha et al.(1991), Seider(1993)는 회전관입말뚝의 지지력과 나선형 판의 간격비에 대한 거동특성을 평가하였다. Perko(2009)는 나선형 회전관입말뚝의 한계깊이를 나선형 회전관입말뚝의 평균 직경과 단위중량과의 관계식으로 나타냈으며, Parry(1977)는 조립토의 극한지지력을 표준관입시험 결과 값의 관계식을 이용하여 산정하였다.
나선형 회전관입말뚝의 축에 발생하는 마찰력에 대한 연구로 Ghaly and Clemence(1998)는 깨끗한 조립의 모래질 지반에서 회전관입말뚝의 축에 발생하는 부착력을 확인하였으며, Narasimha et al.(1993)에 의하면 축 부착력은 사용될 수 있지만 제한적이어야 한다고 밝혔으며, Zhang(1999)은 유효축길이를 결정하였다.
회전관입형 말뚝의 회전저항력과 지지력의 관계는 공공기관의 보고서로 처음 발표되었으며, Hoyt and Clemence(1989)는 회전저항력과 지지력의 관계는 축 직경에 가장 의존적인 것으로 고려하였다. 또한 Hargrave and Thorsten(1992)은 나선형 판의 인발 및 압축거동에 대해 평가하였으며, Perko(2000)는 에너지 보존의 원리를 이용하여 설치시 회전저항력과 지지력의 관계를 평가하였다.
회전관입말뚝의 국내 ‧ 외 선행연구 조사결과, 회전관입말뚝의 기하학적인 특성에 대한 연구와 실내시험 및 현장시험시공의 사례들을 통하여 회전관입말뚝의 지지거동에 대한 연구가 지속적으로 진행되어 왔다. 본 연구에서는 기존 적용되어 왔던 볼트, 용접 및 플랜지(Flange) 방식의 이음부 연결방식을 끼워 맞춤식인 육각형 이음부로 개발하여 국내지반 특성을 고려한 현장시험을 수행하였으며, 현장적용성 평가를 수행하였다.
회전관입말뚝의 이론적 배경
회전관입말뚝의 지지력 이론
상부지반의 지지력이 충분하지 못하거나 침하가 과도하게 일어나는 도서지역과 같은 경우에는 깊은기초를 설치하여 지지력이 충분히 큰 하부의 토층이나 암반층에 상부구조물의 하중을 전달하게 하며, 이러한 깊은기초에서 가장 일반적인 방법이 말뚝기초이다.
말뚝기초의 지지층이 암반 또는 매우 조밀한 모래나 자갈과 같이 단단하고 굳은 지반인 경우에는 말뚝지지력의 대부분은 선단에 있는 토층의 저항으로부터 얻어지며, 이러한 말뚝을 선단지지 말뚝(End-bearing pile)이라 한다. 반대로 말뚝을 견고한 지지층까지 도달시키지 않고 관입이 가능한 토층의 일부 깊이까지만 타입하면 말뚝지지력은 선단지지력과 주면마찰력에 의해 얻어지며, 이러한 말뚝을 마찰 말뚝(Friction pile)이라 한다.
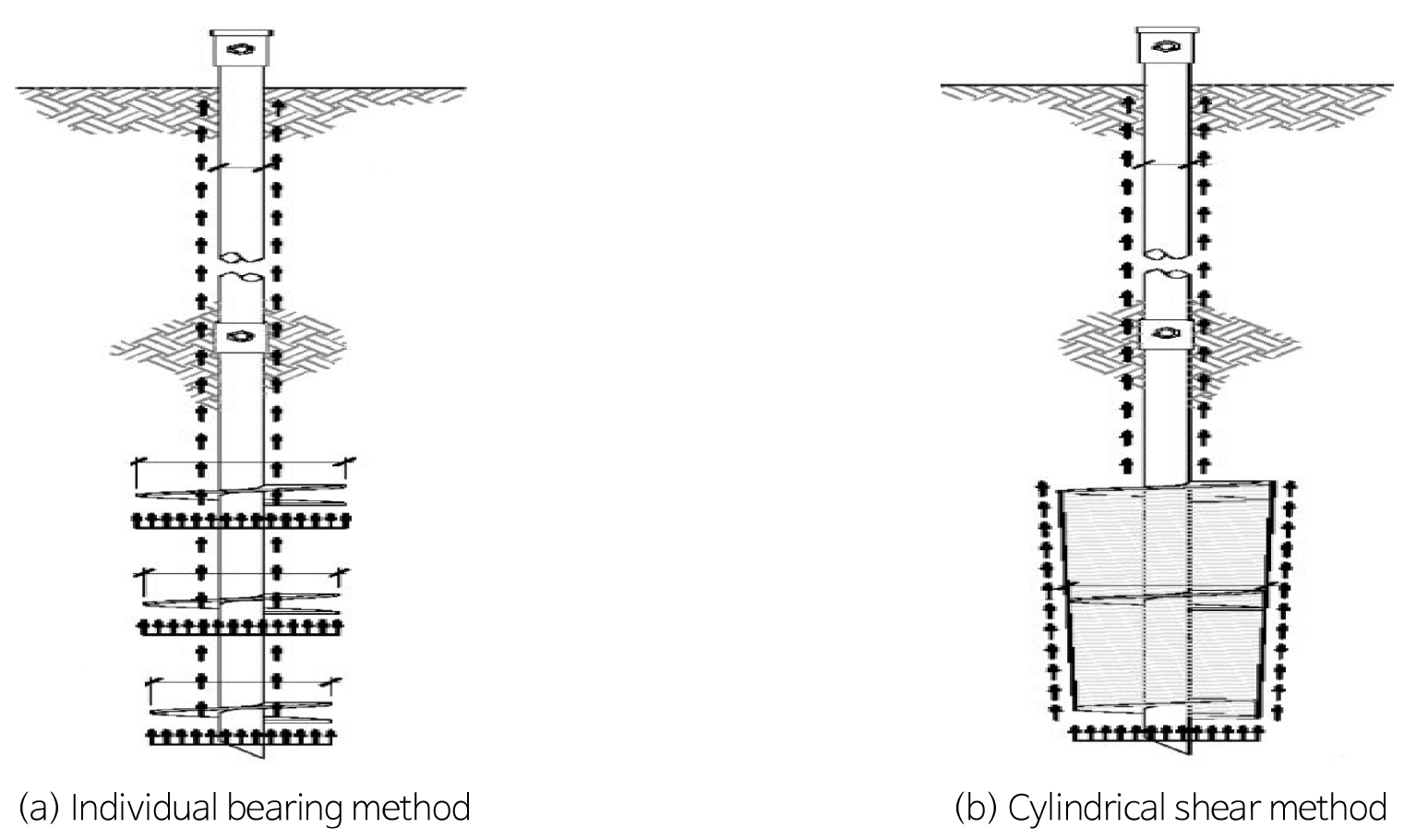
그러나 회전관입말뚝은 중공형 축에 축보다 큰 직경을 갖는 나선형원판이 부착되어 있는 형상으로, 지지력을 발현하는데 있어 축의 주면마찰력 이외에 각각의 나선형 원판이 선단지지력을 발휘할 수 있다. 따라서 Fig. 1과 같이 회전관입말뚝의 지지력 산정법으로는 Individual bearing method, Cylindrical shear method, Torque correlation method가 널리 적용되고 있다.
Individual bearing method는 축에 부착된 나선형 원판이 각각 선단지지력을 발현하여 회전관입말뚝의 지지력을 각 원판의 선단지지력과 축의 주면마찰력의 합으로 산정하는 방법이며, Terzaghi(1943)의 산정식이나 Meyerhof(1951)의 산정식을 사용하고 있다.
Cylindrical shear method는 나선형 원판 사이의 지반전체가 동일하게 저항하여, 원판 사이의 지반에 원통형으로 전단력이 발생하는 것을 가정하여 지지력을 산정하는 방법이다(Mooney et al., 1985).
회전관입말뚝의 개선
기존 기술의 이음부는 강관 모재와 이음부를 핀(Pin) 또는 고장력 볼트, 현장용접에 의하여 연결하는 방식으로서 강관과 이음부가 밀착 ‧ 체결 되지 않아 말뚝의 수직도 확보가 어렵고, 소요지지력 확보를 위한 과도한 회전Torque 발생 시 핀 또는 고장력 볼트의 절단되는 사고가 종종 발생하므로 안전사고 발생의 우려가 있으며, 현장 용접에 의한 인건비 증가와 용접공정 추가에 의한 공사기간의 증가 및 별도의 용접부 품질관리 등 기술적으로나 경제적 측면에서 문제점이 많다.
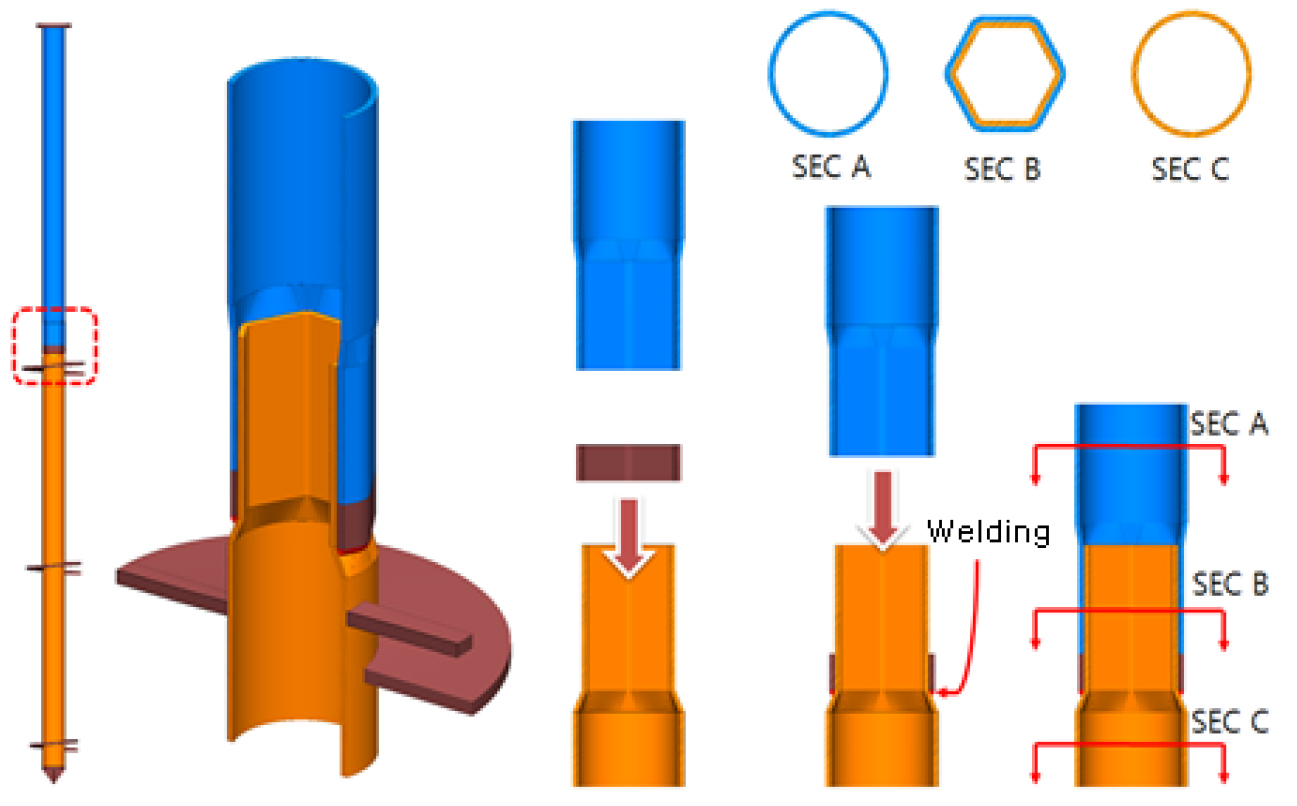
따라서 위와 같은 문제점들을 해결하기 위해 선행연구를 진행해온 바, 획기적인 방식의 이음부가 필요하다는 결론에 이르렀으며, 그 결과를 토대로 원형 강관 말뚝 이음부에 대한 개선방안을 Fig. 2와 같이 고안하였다.
육각형 이음부로 강관 모재의 손실이 없어 축하중 전달이 우수해지고, 이음부에 육각모재가 겹쳐지므로 비틀림 모멘트(Moment)에 대한 회전저항력이 약 2배 증가하여 우수해질 수 있다. 또한 유압잭(Jack) 및 금형을 이용하여 강관의 형태만 변형시키므로 연결부 제작비용이 커플러(Coupler), 볼트, 플랜지 방식에 비해 상당히 절감될 것으로 판단된다.
현장실험
현장실험 개요
본 연구는 육각형 이음부와 중공형 축(D) 165.2 mm 및 원판(D) 450 mm, 400 mm, 350 mm의 원판날개를 갖는 회전관입말뚝을 활용하여 현장 적용성 평가와 국내 지반특성을 고려한 지지력 계산법과 검증을 위해 수행하였다.
대상지역은 Site-1의 경우 전북 정읍시 영원면과 Site-2의 경우 전북 부안군 백산면에 위치한 지방도로건설 현장에서 현장시험시공을 수행하였으며, 시공성 및 지지력을 평가하였다. Site-1과 Site-2의 지질구성을 살펴보면 퇴적토(매립토), 충적층, 풍화토, 풍화암으로 구성되어 있는 대표적인 국내 지반형상으로 해당지역을 현장시험시공 지역으로 선정하였다.
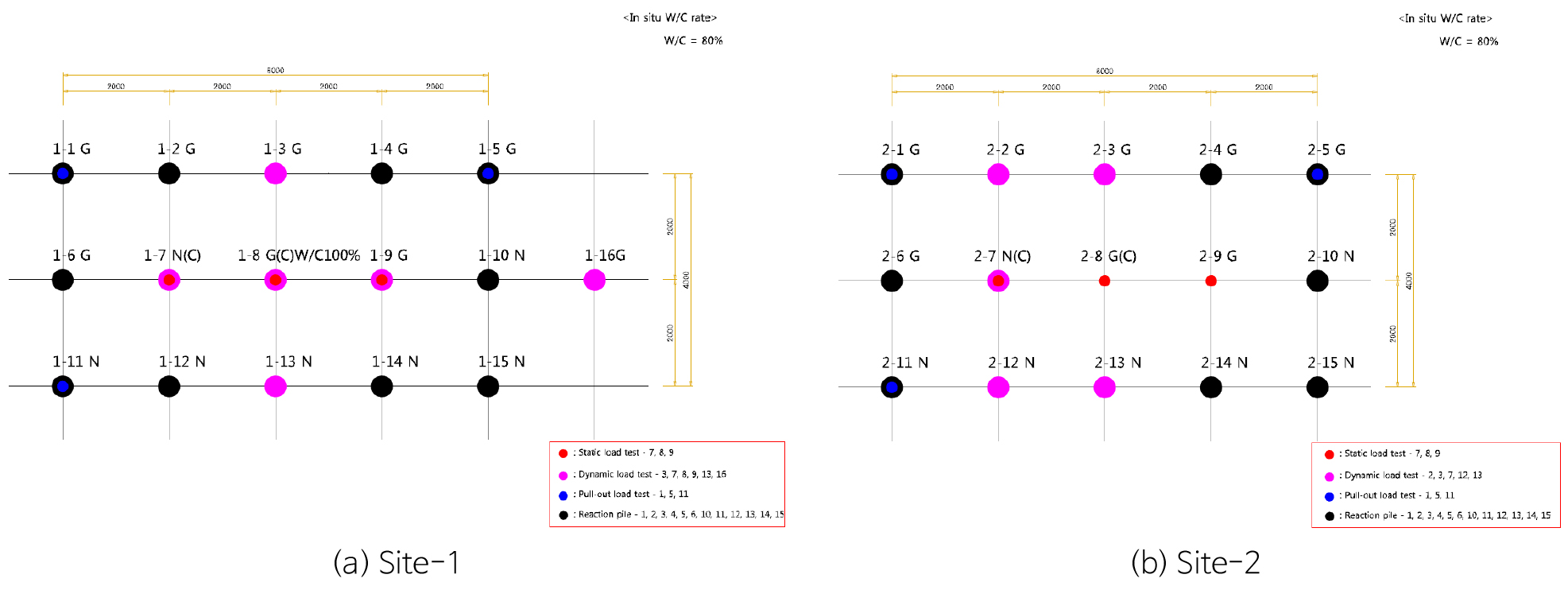
Fig. 3은 현장시험시공 말뚝 배치 계획이다. 말뚝은 각 시험부지에 15본(3 × 5 배열)을 시공하였으며, 말뚝 사이의 간격은 2 m, 압축재하시험 수행 시 인발말뚝을 반력말뚝으로 사용하기 위하여 가운데 열에 압축말뚝을 시공하고 첫 번째 열과 마지막 열에 인발말뚝을 시공하였다.
Table 1은 현장시험시공 계획표이다.
Table 1.
Plan of the in situ test
대상지반의 조건
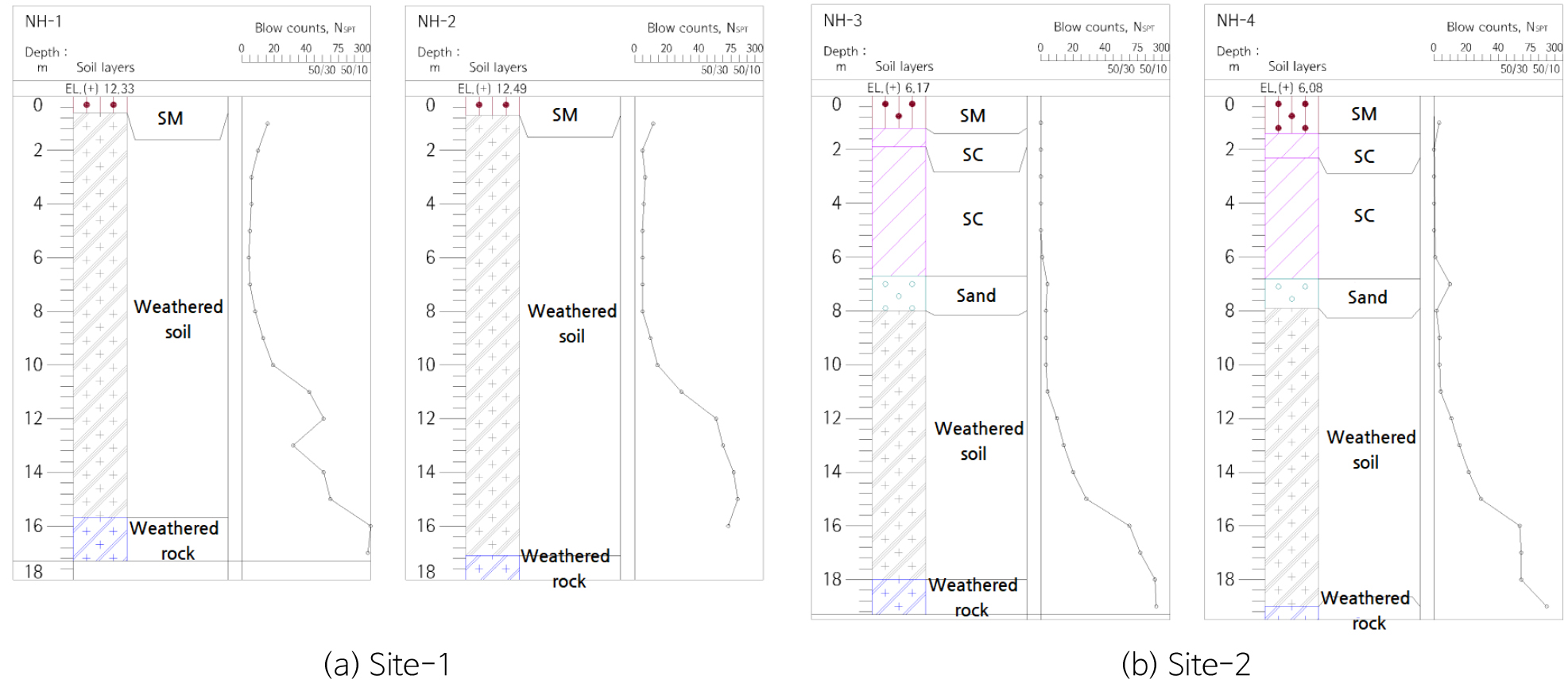
공내지하수위를 측정한 결과, BH-1~2의 경우 지하수위는 지표하 6.00~6.20 m로 풍화토층에 분포하는 것으로 나타났으며, BH-3~4의 경우 지하수위는 지표하 0.70~0.72 m로 매립층에 분포하는 것으로 나타났다.
Fig. 4a와 같이 Site-1의 시추조사 결과, 상부로부터 대략 퇴적층, 풍화토층, 풍화암층 순으로 층구조가 분포하고 있으며, Fig. 4b와 같이 Site-2의 시추조사 결과, 상부로부터 대략 매립층, 충적층, 풍화토층, 풍화암층 순으로 지층구조가 분포하고 있다.
현장시험시공
본 연구에서 사용된 장비는 0.8 m3 버킷(Bucket) 용량의 Back/Hoe(이하 B/H)를 사용하였으며, Fig. 5a는 현장 시험시공 전 현장 부지의 평탄화 작업을 실시한 전경과 시공의 편의성을 위하여 말뚝 시공 위치 주변에 자재를 야적시켰다. Fig. 5b는 회전관입장치(Earth drill 50,000 Max) 연결 모습이다. 본 연구에서 사용한 회전관입장치는 0.8~1.0 m3 버킷 용량의 B/H에서 작동이 가능하며, 유압호스(Hose)를 B/H에 연결하여 사용할 수 있다. Fig. 5c는 나선형 원판이 부착된 선단부 말뚝을 결합하는 모습이며, Fig. 5d는 선단부 말뚝을 회전관입하는 모습이다. Fig. 5e는 육각형 이음부를 끼워 맞춤식 방법으로 시공하는 모습이며, Fig. 5f는 볼트 체결식으로 시공하는 모습이다.
육각형 이음부를 갖는 끼워 맞춤식 방법과 기존 볼트방식의 연결시간 측정결과, 육각형 이음부를 갖는 회전관입말뚝이 3 m 길이당 약 5 min 이상의 공사시간을 절약할 수 있었다. 이는 전체적인 공기의 영향에 미치며 일반적인 회전관입말뚝 시공량은 200 m/day으로 육각형 이음부로 개선된 회전관입말뚝의 시공량은 약 250 m/day 이상으로 수행할 수 있다.
재하시험방법
압축재하시험(정재하시험)
압축재하시험을 위해서는 말뚝 목표하중의 2~3배에 달하는 재하하중이 필요하다. 재하방법으로는 사하중을 재하하는 방법, 반력말뚝의 주면마찰력을 이용하는 방법, Earth Anchor의 인발저항력을 이용하는 방법이 있으나, 본 연구에서는 반력말뚝의 주면마찰력을 이용하는 방법으로 수행하였다. 또한 파괴하중을 결정하기 위해 목표하중의 3배 하중을 최대 시험하중으로 결정하였으며, 하중의 재하 및 제하방법은 KS 2445 및 ASTM D1143 규정에 근거한 급속재하시험 방법으로 수행되었다.
재하시험은 총 3 Cycle로 계획하였으며, 각 단계별 재하하중 유지시간은 5분으로 하여 1분 간격으로 침하량을 기록하였으며, Creep를 고려하여야 하는 경우 목표하중의 100%, 200%에서 60분간의 침하량을 기록하였다.
인발재하시험
본 연구에서 개발한 직경 165.2 mm (t = 7.5 mm)의 현장 적용성 평가를 위해 회전관입말뚝을 2개의 시험시공부지에 각각 15본씩을 시험시공하고 부지별로 3본씩, 총 6본에 대하여 인발재하시험을 실시하였다.
시험말뚝은 일반구조용 탄소강관(KS D 3566)의 STK490을 사용하였으며, 직경은 165.2 mm, 두께는 7.5 mm, 나선형 원판의 직경은 각각 450 mm, 400 mm, 350 mm, 나선형원판의 두께는 20 mm이다.
재하시험은 지반 접지압을 반력으로 이용한 재하시험방법으로 수행되었으며, 파괴하중을 결정하기 위해 목표하중의 3배 하중을 최대 시험하중으로 결정하여 급속재하시험 방법으로 수행되었다.
현장실험 결과
압축재하시험 결과
안전율 적용 기준에 따른 압축재하시험 지지력 비교결과
압축재하시험을 이용한 허용지지력 평가 시 적용되는 안전율에 대한 각 국가별 적용기준은 다르며, 말뚝의 형태와 시공방법에 따라 달리 적용해야 한다. 본 연구에서 수행한 회전관입말뚝은 철저한 지반조사를 통해 Individual bearing method에 의해 설계지지력을 산출한 결과 설계지지력은 600.0 kN이었다. 따라서 허용지지력 평가 시 적용되는 여러 가지 규정에 따른 지지력과 회전관입말뚝 특성을 고려한 AC 358 Code와 Livneh and Naggar(2008) 규정으로 기존 방법과 지지력을 비교하였다.
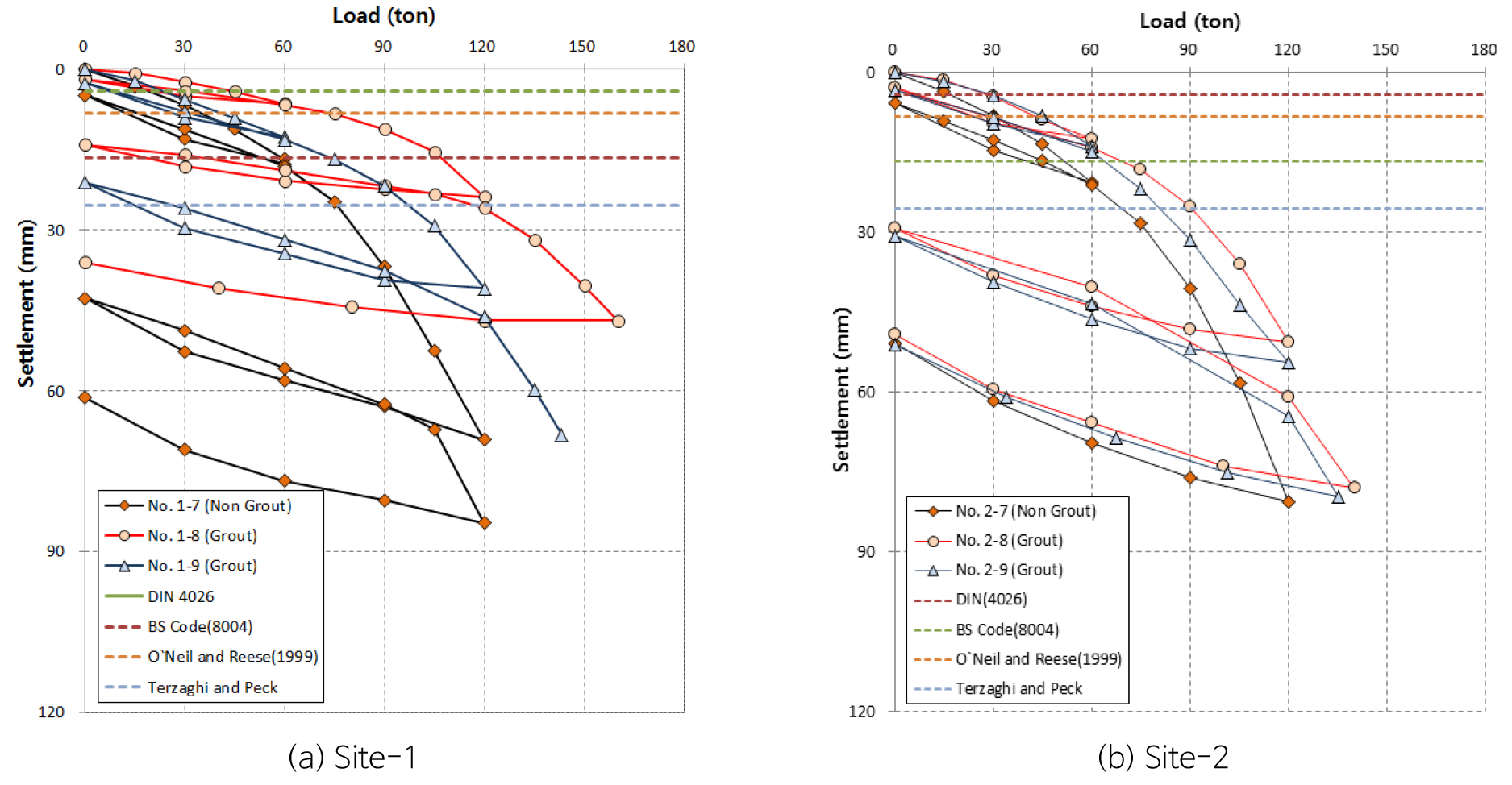
Fig. 6은 말뚝 직경 기준에 따른 지지력 평가를 수행하였다. 본 회전관입말뚝은 말뚝의 직경이 165.2 mm로 강소말뚝에 해당하며, 지지력이 상당히 낮게 평가됨을 확인할 수 있었다. 이는 전침하량 기준의 방법은 일반적으로 말뚝의 직경이 300 mm 이상에서 보편적으로 적용되기 때문에 말뚝 직경이 큰 경우 적합한 방법으로 판단된다.
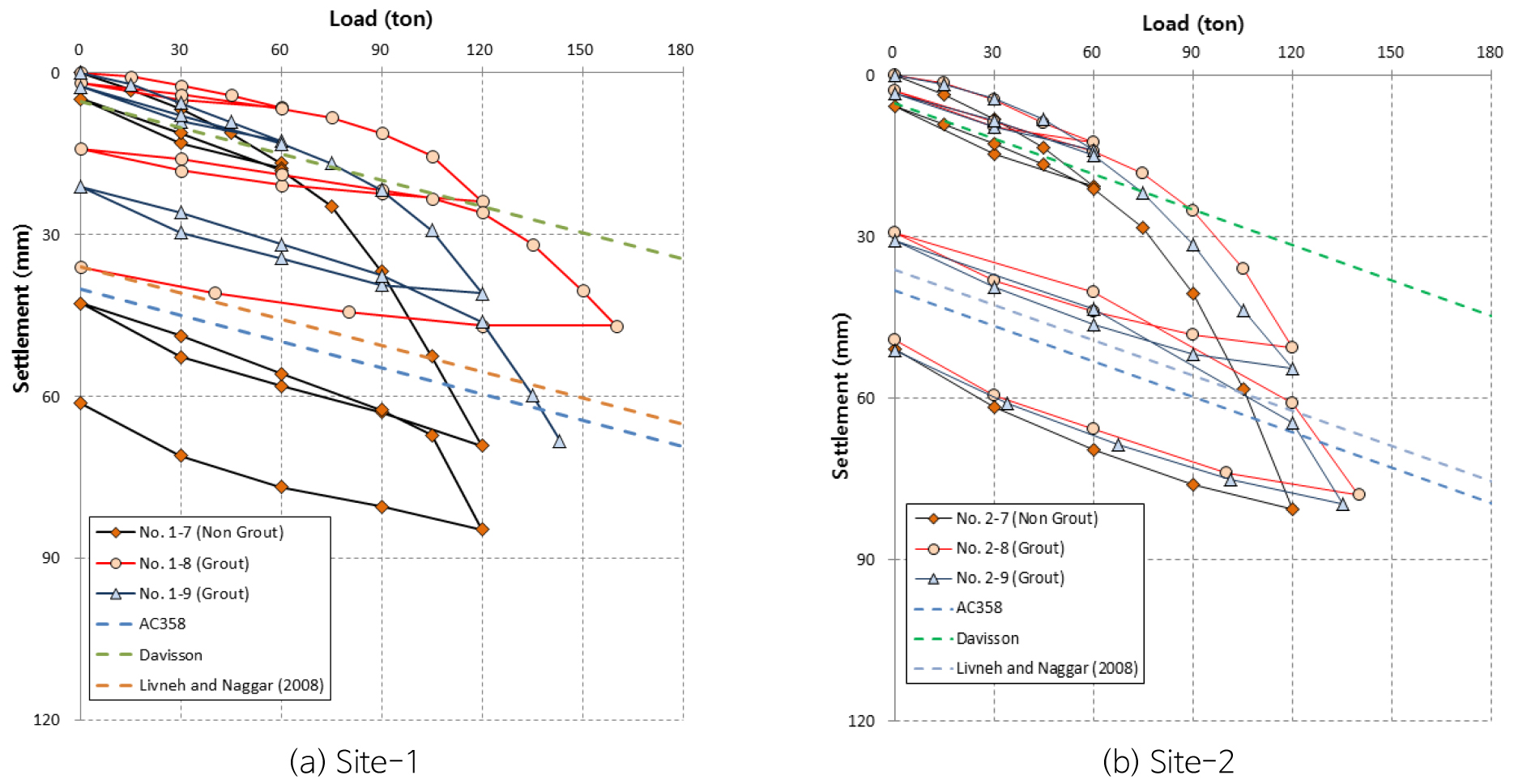
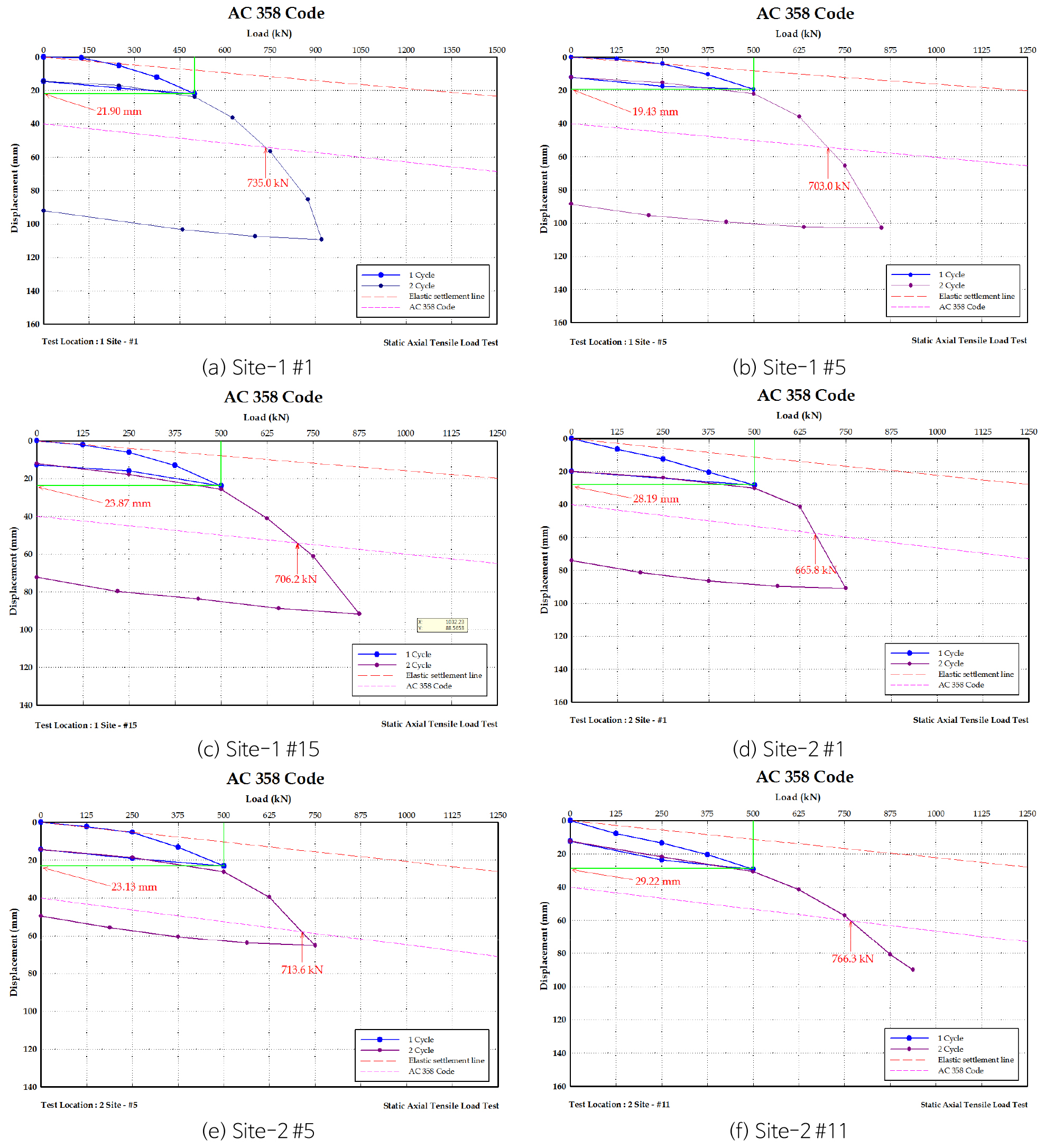
Fig. 7은 Davisson’s method를 활용한 나선형 원판 기준에 따른 지지력 평가를 수행하였다. 국외 선행연구결과, 회전관입말뚝 특성상 나선형 원판을 이용한 기준은 AC 358 Code와 Livneh and Naggar(2008)의 방법이 있었으며, AC 358 Code를 적용한 경우 Individual bearing method로 설계한 600.0 kN과 가장 유사한 지지력 값을 나타냄을 확인하였다. 따라서 본 연구에서의 재하시험의 결과는 AC 358 Code를 적용하여 지지력을 평가하였다.
본 압축재하시험은 주변말뚝의 인발저항력을 이용한 압축재하시험방법으로 수행되었으며, 파괴하중을 결정하기 위하여 목표하중의 3배 하중을 최대시험하중으로 결정하여 급속재하시험 방법으로 수행되었다.
Site-1, Site-2 시험말뚝에 대해 수행된 압축재하시험결과, 중력그라우트를 실시한 말뚝에서 허용지지력은 Site-1의 경우 각각 678.6~800 kN/본, Site-2의 경우 각각 627.3~664.7 kN/본으로 확인되었으며, 중력그라우트 미실시 말뚝에서 허용지지력은 Site-1, 2 각각 553.3 kN/본, 554.2 kN/본으로 확인되었다. 따라서 회전관입말뚝 시공 시 중력그라우트를 실시하는 것이 바람직 할 것으로 판단되며, 중력그라우트 실시말뚝들의 경우 목표하중인 600.0 kN 재하 시 허용침하량 기준인 1 inch (25.4 mm) 이내로 발생한 것으로 확인되어 침하에 대해서도 안정할 것으로 판단된다.
특히 풍화암에 근입된 것으로 추정되는 1-#8 말뚝의 경우, 목표하중의 2배 재하 시에도 허용침하량(25.4 mm) 이내로 침하가 발생하여 회전관입말뚝을 풍화암에 지지할 경우 좀 더 큰 허용지지력을 확보할 수 있을 것으로 판단된다. 이에 회전관입에 의한 시공된 말뚝을 풍화암에 지지할 수 있는 방법을 고안하여 좀 더 큰 목표하중에 도달할 수 있는 추가 연구가 필요할 것으로 판단된다.
Table 2는 압축재하시험 결과이다.
Table 2.
Results of the static pile load test
인발재하시험 결과
본 인발재하시험은 지반 접지압을 반력으로 이용한 인발재하시험방법으로 수행되었으며, 파괴하중을 결정하기 위해 목표하중의 3배 하중을 최대시험하중으로 결정하여 급속재하시험 방법으로 수행되었다.
Fig. 8과 Table 3과 같이 Site-1 말뚝들의 경우 허용인발력은 351.5~367.5 kN/본으로 확인되었으며, Site-2 말뚝들의 경우 허용인발력은 332.9~383.2 kN/본으로 확인되었다.
Table 3.
Results of pull-out pile load test
결 론
본 연구에서는 중공형 축의 모형을 육각형 이음부로 개선하여 압축재하 시 별도의 용접이나 볼트가 필요 없는 방식으로 개선하였으며, 국내 지반에서 적용하기 위해 현장시험을 통한 압축재하 및 인발재하시험을 측정하여 현장적용성에 대한 평가를 수행하였으며, 분석결과 다음과 같은 결론을 얻었다.
(1) 육각형 이음부를 갖는 끼워 맞춤식 방법과 기존 볼트방식의 연결시간 측정결과, 육각형 이음부를 갖는 회전관입말뚝이 3 m 길이당 약 5 min 이상의 공사시간을 감소할 수 있다. 이는 전체적인 공기의 영향에 미치며 일반적인 회전관입말뚝 시공량은 200 m/day으로 육각형 이음부로 개선된 회전관입말뚝의 시공량은 약 250 m/day 이상으로 수행할 수 있다.
(2) 현장재하시험을 통한 압축재하시험 분석 결과, 중력 그라우트를 실시한 말뚝에서 확인된 허용지지력은 구릉지의 경우 678.6~800 kN/본, 충적지의 경우 627.3~664.7 kN/본으로 확인되었으며, 중력 그라우트 미실시 말뚝에서 확인된 허용지지력은 구릉지, 충적지 모두 목표하중인 600.0 kN/본 미만으로 나타나 회전관입말뚝 시공 시 중력 그라우트를 수행해야 할 것으로 판단된다. 또한 목표하중인 600.0 kN 재하 시 허용침하량 기준인 1 inch (25.4 mm) 이내로 발생한 것으로 확인되어 침하에 대해서도 안정할 것으로 판단된다.
(3) 현장재하시험을 통한 인발재하시험 분석 결과, 구릉지 말뚝들의 경우 허용인발력은 351.5~367.5 kN/본, 충적지 말뚝들의 경우 332.9~383.2 kN/본으로 확인되었다. 따라서 목표하중인 500.0 kN/본에 미치지 못하였으나, 이는 압축재하시험 시 반력말뚝으로 1회 사용되어 인발저항력이 낮게 나타난 것으로 판단된다.
(4) 본 현장시험 결과는 적은 표본에 의해서 도출된 결과로 추후 기초자료로 활용될 수 있을 것으로 판단되며, 더 많은 현장시험 결과를 바탕으로 지반조건에 따라 지지력을 비교 분석하면 신뢰성 있는 회전관입말뚝의 경험적 지지력 산정식을 제안할 수 있을 것으로 판단된다.