Introduction
Interpolation Methods
Linear Combination of Values
Radial Basis Function
Comparison of Interpolation Methods
Test Functions and Data Sets
Results of Test and Discussion
Application of Interpolation Methods
Conclusion
Introduction
Spatial interpolation is essential in many scientific and engineering fields to ensure the accurate and effective evaluation of physical data in a continuous domain. Numerous spatial interpolation techniques have been introduced, with these approaches possessing various degrees of complexity (Lam, 1983; Myers, 1994; Webster and Oliver, 2007; Li and Heap, 2008); however, selecting the best technique that produces reliable and accurate results is difficult. While various studies have attempted to construct mechanisms for choosing and evaluating the methods that best suit the actual data (Caruso and Quarta, 1998; Li and Heap, 2011), the various factors that affect the performance of spatial interpolations generally indicate that no method is always optimal for specific situations. A method that works well with one dataset may be unsuitable for a different dataset because the interpolated results are strongly dependent on the characteristics of the data. Therefore, comparative studies have recently focused on identifying the optimal method for specific objects of a given study. For example, Sun et al. (2009) compared interpolation methods using data obtained over 22 years on the temporal and spatial variations of groundwater depth in a specific study area. Tabios III and Salas (1985), Keblouti et al. (2012), and Wagner et al. (2012) evaluated various methods to find the most appropriate interpolation method for sparse precipitation data. Piazza et al. (2011) conducted a comparative study on various methods for the estimation of missing data in rainfall time series. Teegavarapu et al. (2012) developed and estimated spatial interpolation weighting methods for the transformation of hourly multisensory precipitation data from one grid to another with different sizes and orientations. Rap et al. (2009) compared interpolation methods for aerosol-cloud parameterization in global climate modeling.
As computational techniques have improved, numerical simulations have grown in popularity in many disciplines and are used as preliminary or predictive tools for specific purposes. Continuous natural objects or characteristics, which are generally obtained from field measurements at scattered points, must be assigned to discrete nodal points for numerical modeling where interpolation is used for data pre-processing. An interpolation may also be required after the simulation to compare the calculated results with observed values. The number of nodal points has increased from dozens or hundreds to thousands or more as more detailed modeling is being undertaken to evaluate datasets. Furthermore, if time is included as a variable, as done in transient modeling, then the data processing requirements can increase nonlinearly. Therefore, a faster and more accurate interpolation method is required to effectively evaluate large datasets. Alternatively, the model domain can be decomposed into several regions, thereby allowing the necessary interpolations to be performed within a targeted sub-region (Mitášová and Mitáš, 1993; Trochu, 1993).
This study proposes a new method using irregular quadrilateral elements to address existing limitations to interpolation. This method is based on the interpolation technique used in finite element methods and can be applied to both rectangular grids and irregular meshes in finite-difference, finite-volume, and finite-element methods. This proposed method, hereafter called the quadrilateral irregular network (QIN), is similar to the triangular irregular network (TIN), which is a well-known conventional method. After introducing the QIN, conventional methods for the linear combination of values, such as TIN and the inverse distance weight method as well as methods based on radial basis functions, such as thin plate spline (TPS), completely regularized spline (CRS), dual kriging (DK), and Hardy (1971)’s multiquadric method (HMQ), are briefly summarized. The QIN and other methods are then estimated using the well-known Franke (1979) test functions, and applied to the results of numerical modeling for a comparison of their effectiveness in interpolating spatial data.
Interpolation Methods
Linear Combination of Values
Linear combination interpolation methods share the same general form as follows:
where u* is the interpolated value of a variable at a target point (x, y), u is the known value at the i-th sampled point (xi, yi), λi is the weight assigned to the i-th sampled point, and N is the number of sampled points used for the interpolation.
Quadrilateral Irregular Network (QIN)
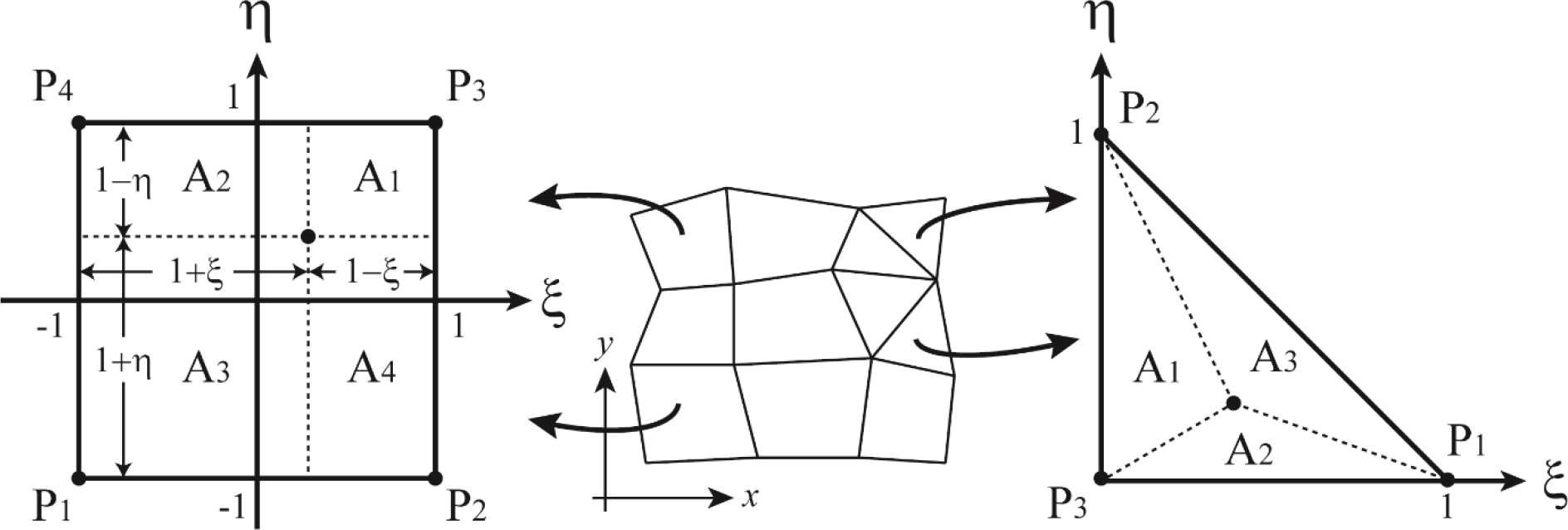
Finite element processes generally transform each quadrilateral element in a global coordinate system to a square isoparametric element that is defined in a ξ-η local coordinate system, as shown in Fig. 1. These local coordinates, ξ and η, are used to determine the sampling points of the Gaussian quadrature, which is a way to numerically approximate the value of an integration. A value (u) within a quadrilateral element is estimated from the nodal values of the isoparametric element as follows:
where Ne (= 4 for linear quadrilateral elements) is the number of nodes in an element, ui is the known value at the i-th nodal point, and Ni(ξ, η) is the i-th shape function for a local element, which is defined in bilinear form (Becker et al., 1981; Heinrich and Pepper, 1990) as follows:
Eqs. (1) and (2) are of the same form, except for the number of points used for the interpolation. The weights of the quadrilateral elements are determined by the ratio of the areas diagonally opposite the corresponding nodes to the total area, for example, N1 = A1/4 (see Fig. 1). Using Eq. (2), points in the local coordinate system can be mapped to corresponding points in the actual global coordinate system as follows:
Therefore, the values of x, y, and variables in the global coordinate system can be easily estimated at a given point (ξ, η) within an isoparametric element through Eqs. (2), (3), (4), (5). However, for a point (x, y) within an irregular-shaped quadrilateral element in the global coordinate system, estimation of variables at a given point is difficult because the local coordinate values (ξ, η) corresponding to the point are not known. Therefore, inverse mapping is necessary to estimate the variables.
Substitution of Eq. (3) into Eqs. (4) and (5) yields:
respectively, where the coefficients are a1 = (x1 + x2 + x3 + x4)/4, a2 = (-x1 + x2 + x3 - x4)/4, a3 = (-x1 - x2 + x3 + x4)/4, a4 = (x1 - x2 + x3 - x4)/4, b1 = (y1 + y2 + y3 + y4)/4, b2 = (-y1 + y2 + y3 - y4)/4, b3 = (-y1 - y2 + y3 + y4)/4, and b4 = (y1 - y2 + y3 - y4)/4. Coefficients ai and bi are known values from four nodal coordinates of a quadrilateral element. Therefore, if the coordinate values (x, y) of an arbitrary point are given, then Eqs. (6) and (7) become non-linear equations of ξ and η. Although the numerical solution for ξ and η can be obtained through the iterative Newton-Raphson method, there is a possibility that a convergent solution cannot be obtained due to numerical error. Therefore, an analytic solution for ξ and η should be considered instead of an iterative numerical solution.
The quadratic equation for ξ such as Eq. (9) can be obtained by rearranging Eq. (6) for η and substituting the resultant Eq. (8) into Eq. (7).
where the coefficients A = a2b4 - a4b2, B = a2b3 - a3b2 + (a1 - x)b4 - a4(b1 - y), and C = (a1 - x)b3 - a3(b1 - y). The solution for ξ is as follows:
If a quadrilateral element is defined in a counterclockwise direction, then the positive square root should be applied to Eq. (10). Conversely, if a quadrilateral element is defined in a clockwise direction, the negative square root should be chosen as the solution for ξ. In addition, if coefficient A in Eq. (9) equals zero, then the quadratic equation is reduced to a linear equation, and the solution for ξ becomes:
Coefficient A = 0 is equal to u1v2 - u2v1 = 0 when coefficient A is expressed by the components of vector u and v in Fig. 2a for a detailed geometrical configuration. This means that u × v = 0, that is, the two vectors are parallel. Once ξ is obtained using Eq. (10) or Eq. (11), η can be estimated from Eq. (8). However, η cannot be calculated when the denominator in Eq. (8) equals zero. In this case, another approach for estimating η should be considered.
The first condition that results in a zero denominator is when a3 = a4 = 0. By applying this condition to Eq. (6), a simplified equation such as x = a1 + a2ξ can be obtained. Therefore, substituting ξ = (x - a1)/a2 into Eq. (7) and rearranging the equation yield the following:
To explain the geometrical meaning of this condition, the coefficients a3 and a4 can be expressed as components of vectors p and q in Fig. 2a:
The condition a3 = a4 = 0 is only satisfied when p1 and q1 both equal zero, which means that p and q are parallel to both each other and the vertical axis.
The second condition is a3 = ξ = 0 and a4 ≠ 0. Substituting this condition into Eq. (6) shows that this situation occurs when x = a1. Substituting ξ = 0 into Eq. (7) and rearranging the equation yield as follows:
This is the same as Eq. (12) when a1 - x = 0. Geometrically, only a3 may be zero when components p1 and q1 of vectors p and q in Fig. 2a are equal in magnitude and in opposite directions, as can be inferred from Eq. (13).
The third condition is when a3 ≠ 0 and a4 ≠ 0, but a3 + a4ξ = 0. Applying ξ = -a3/a4 to Eq. (6) and Eq. (7), respectively, yield x = a1 - (a2a3)/a4 and the relation for η as follows:
It may be inefficient and time-consuming to compute ξ and η in all elements to find the element in which an arbitrary point is located. This is especially true when the number of elements is very large. Therefore, either rectangles or circles enclosing an element are utilized in this search. As shown in Fig. 3a, two opposite corners of a rectangle enclosing an element are compared with the coordinate (x, y) of an arbitrary point. It is then temporarily determined that an arbitrary point may be located within the element when the following inequality is satisfied:
Alternatively, the center coordinates of the circumcircle are necessary when using circles that enclose an element. As shown in Fig. 2b, vectors u and v1 and vectors w and v2 are perpendicular to each other, respectively, based on the definition of the circumcircle. That is, u ∙ v1 = 0 and w ∙ v2 = 0, and the following system of linear equations is derived.
where Δvi1 = vi - v1, = (vi + v1)/2, and xc and yc are the center coordinates of the circumcircle. Two circumcircle radii can be obtained through Eq. (17) when a quadrilateral is divided into two triangles, as shown in Fig. 3b. If the distance between one of the center points of the circumcircles and an arbitrary point is less than or equal to the radii of the circumcircles, it is temporarily determined that an arbitrary point may be located within the element, and the exact values of ξ and η can be estimated analytically. If both ξ and η are in the range of [-1, 1], then an arbitrary point is definitely within the quadrilateral element, and the variables can be estimated by using Eq. (2).
Triangular Irregular Network (TIN)
It is simpler to find local coordinates within triangular elements than within quadrilateral elements. The local coordinates ξ and η within a triangular element can be estimated directly from global coordinates as follows (Becker et al., 1981; Heinrich and Pepper, 1990):
As with quadrilateral elements, the areal ratio is also used for triangular elements. An arbitrary point is within a triangular element when ξ and η satisfy the following inequality:
If so, some values at an arbitrary point are interpolated from the nodal values of an isoparametric triangular element by using Eq. (2). The shape functions for triangular elements are as follows:
which are the same as the quadrilateral elements in that the ratio of the areas diagonally opposite from the corresponding nodes to the total area is used as a weight (see Fig. 1). As in the quadrilateral, it can be preliminarily evaluated whether or not an arbitrary point is located within the element by using either a rectangle or circle that encloses a triangular element.
Inverse Distance Weight Method
In distance weighting interpolation methods, the weight of the i-th sampled point is defined as a function of the distance from the target point to the sampled points, given in general as follows:
where function f(di) is defined as dip, and di is the distance from the target point to the i-th sampled point. When the power parameter p of -2 or -1 is selected, this is called the inverse square distance (ISD) or reciprocal distance weight (RDW) method, respectively. Therefore, the weights diminish as the distance increases, and the values sampled nearby have more influence on the estimation. When the target point coincides with one of the sampled points, the value of the target point should take the value of the sampled point because the weight becomes infinite. For wide areas or for large data sets, the searching radius or threshold distance (dmax) may be set (Caruso and Quarta, 1998), and the function of distance is defined as follows:
This situation is called localized ISD or localized RDW (Wagner et al., 2012).
Radial Basis Function
Interpolation functions based on the radial basis function have the following general form (Talmi and Gilat, 1977; Mitášová and Mitáš, 1993):
where R(∙) is a radial basis function, T(∙) is called the trend function, fk(∙) is a set of linearly independent monomial functions, and αk and βj are coefficients. Once the radial basis function is determined, the coefficients αk and βj can be obtained by solving the following system of linear equations.
In a geostatistical framework, Eq. (25) is called a drift, the second term on the right hand side of Eq. (24) is called a fluctuation, and the function R(∙) within the second term on the right hand side of Eq. (24) is replaced with the function K(∙), which is called the generalized covariance. The final M equations in Eq. (26) are called the no-bias condition, which shows that the trend function or drift represents the mean of sampled values. Therefore, the fluctuation term is adjusted so that the interpolation coincides with the data points (Trochu, 1993).
Thin Plate Spline (TPS)
Duchon (1976) proposed the following trend and radial basis functions for the TPS interpolation method.
Therefore, coefficients αk (1 ≤ k ≤ 3) and βj (1 ≤ j ≤ N) in Eq. (24) are characterized by the following linear system.
Completely Regularized Spline (CRS)
Mitášová and Mitáš (1993) derived a new interpolation method called the completely regularized spline as an alternative method to regularized TPS with tension which was developed to compensate for the shortcomings of TPS by Mitáš and Mitášová (1988). The trend and radial basis function of CRS are as follows:
where E1(∙) is the exponential integral function found in Abramowitz and Stegun (1972), CE is the Euler constant of 0.5772156649, and φ is a generalized tension parameter that should be determined empirically. Consequently, coefficients αk (k = 1) and βj (1 ≤ j ≤ N) in Eq. (24) can be obtained from the N + 1 linear equation.
Dual Kriging (DK)
Trochu (1993) proposed the following generalized covariance for the 2-D case derived from TPS in order to incorporate the distance of influence in his dual kriging model.
where c1 is a constant of 0.18393972, and c0 is a constant of 0.60653066, which is the value when the function d2lnd attains its minimum; -c1 = c02lnc0. The function R(∙) in Eq. (32) continuously decreases from 1 when dj = 0 to 0 when dj > dmax. As in TPS, the values of coefficients αk and βj in Eq. (24) can be obtained by solving N + 3 linear equations.
Hardy’s Multiquadric (HMQ) Method
Hardy (1971) proposed the following relatively simple function for the interpolation of irregular surfaces.
Eq. (33) represents the multiquadric surface, which is a single cone or hyperboloid dependent upon whether Δ2 equals zero or is a positive constant, respectively. In HMQ, the trend function of Eq. (25) is zero. Therefore, βj (1 ≤ j ≤ N) in Eq. (24) is obtained by solving linear equations of order N. For reference, the method of applying a power of -1/2 instead of 1/2 to the right side of Eq. (33) is called the reciprocal multiquadric (RMQ) method, and successful applications of HMQ in various disciplines can be found in Hardy (1990).
Comparison of Interpolation Methods
Test Functions and Data Sets
The comparison of interpolation methods described in the preceding chapter is based on the six test functions used by Franke (1979) in his critical comparison of interpolants for scattered data, reported as:
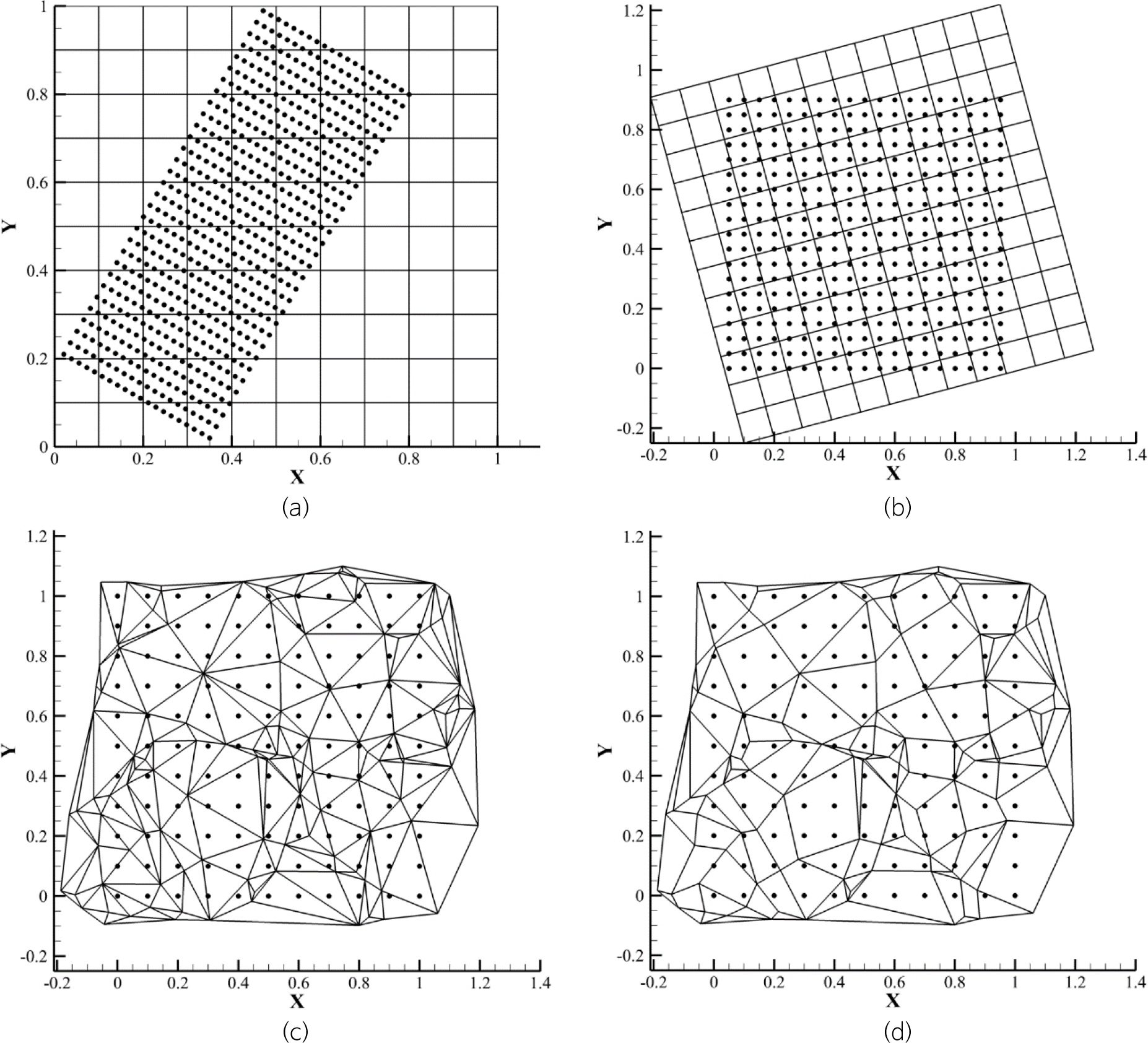
Four of the six test functions (test functions 2 and 4-6) were originally provided by McLain (1974), then slightly modified and scaled down from [1, 10] to [0, 1] by Franke (1979). A total of three grid networks were constructed as shown in Fig. 4. The first case is an 11 × 11 square grid, which has an origin of (0, 0) with both a horizontal (Δx) and vertical (Δy) interval of 0.1, whereby 121 total points were used to generate the test function values in Eq. (34). The known values in the sparse square grid were then interpolated into points on a fine grid that was rotated 60° counterclockwise from the horizontal axis and consisted of 20 rows and 31 columns, with its origin at (0.35, 0.02), Δx = 0.03 and Δy = 0.02 (Fig. 4a). The second case is a 13 × 13 square grid that was rotated 15° counterclockwise from the horizontal, with its origin at (0.1, -0.25), and Δx = Δy = 0.1. The 169 generated values were then interpolated to points on a 19 × 19 fine square grid, with its origin at (0.05, 0.0), Δx = Δy = 0.05, and no rotation (Fig. 4b). The third case is a mesh grid consisting of 120 randomly generated points. The triangular elements were constructed from the distribution of these points over the entire area, with some triangles then combined into quadrilateral elements for the QIN application. Therefore, the third case was divided into a fully triangular element mesh (Fig. 4c) and a mixed mesh with triangles and quadrilaterals (Fig. 4d). The nodal values were interpolated to points on an 11 × 11 square grid, with its origin at (0.0, 0.0), Δx = Δy = 0.1, and no rotation. Therefore, both pure TIN and a combination of QIN and TIN (hereafter QIN&TIN) were applied to the third case, whereas only QIN was used for the first and second cases.
Results of Test and Discussion
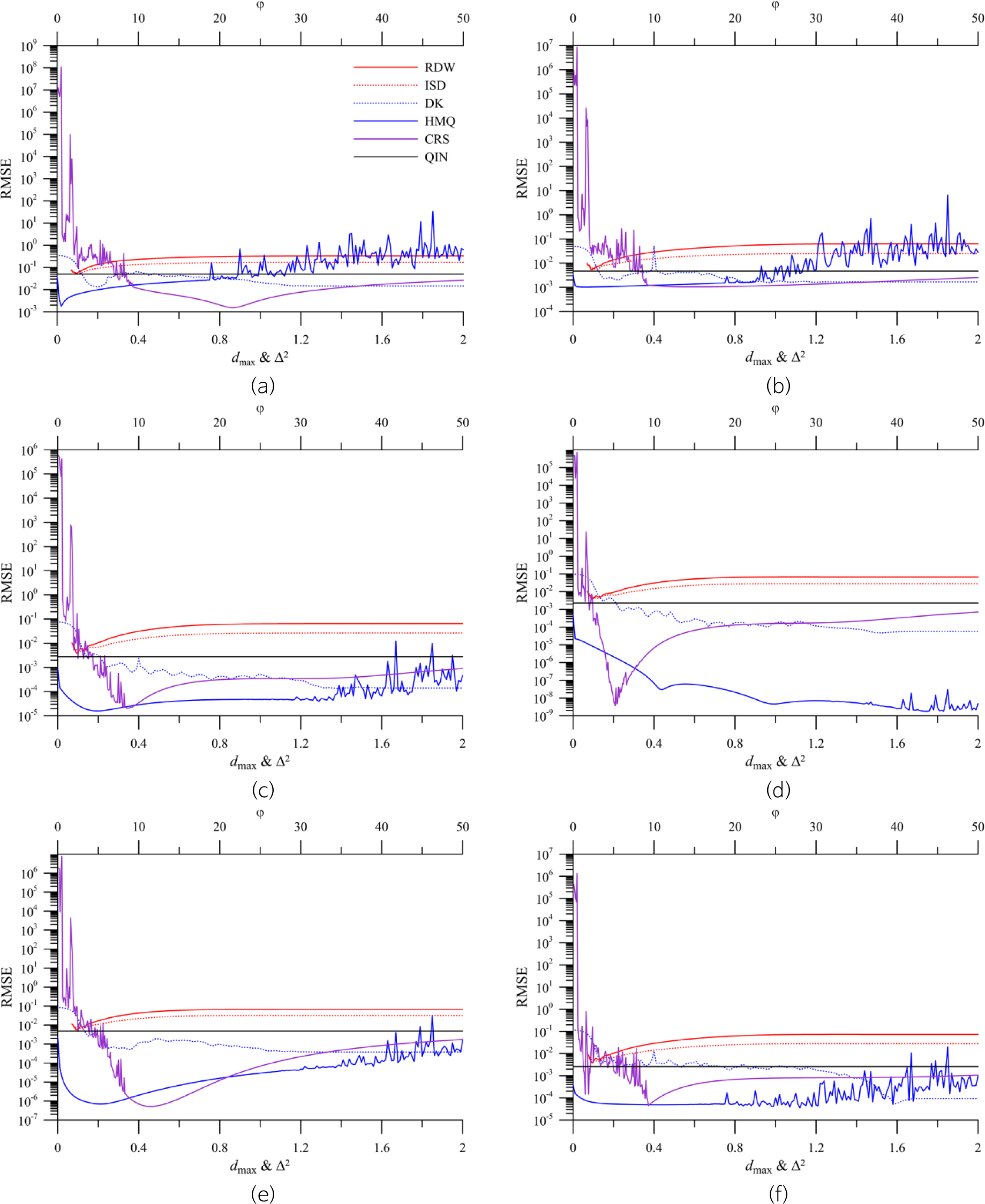
The sensitivity analysis results, presented as a function of a given parameter for each interpolation method and test case, are shown in Figs. 5, 6, 7. The lower horizontal axis is the searching radius (dmax) for DK, RDW, and ISD and the parameter value (Δ2) for HMQ, and the upper horizontal axis is a generalized tension parameter value (φ) for CRS. The vertical axis represents the corresponding RMSEs on a logarithmic scale. The resultant QIN (cases 1 and 2), and QIN&TIN and TIN (case 3) RMSEs, which appear as constant values, are provided for comparison with the other methods.
At first, the methods using a searching radius are discussed. With RDW or ISD, the most accurate results were obtained with dmax of about 0.1 for the first and second cases, and about 0.2 for the third. As dmax increases from these values, the accuracy of the interpolants decreases. Eventually, the effect of the searching radius disappears from around 0.6. It is difficult to find the optimal dmax when RDW or ISD is applied to complex natural phenomena. Therefore, in many practical applications of RDW and ISD, weighting coefficients are generally calculated using all data points without considering the searching radius. Although RDW and ISD are well-known and popular methods due to their practical simplicity, they seem to be the least sophisticated among all of the methods tested in this study when the searching radius is not considered. Trochu (1993) introduced the searching radius for geostatistical kriging in order to account for the distance of influence and, as a result, reduced the computational effort due to the derivation of banded structures in the kriging matrix. He mentioned that dmax should be selected carefully because it controls the smoothness of the interpolation, the loss in accuracy may be unacceptable when dmax is small, and there is no difference between the results with and without the distance of influence when dmax greater than a certain threshold value is selected. However, he did not indicate a specific value or range as the optimal dmax for DK. As shown in Figs. 5, 6, 7, the accuracy of DK is improved as dmax increases, reaching an asymptotic constant equal to the RMSE of TPS. Therefore, to avoid the ambiguity of dmax as a parameter and the effort of trying to find the proper value for dmax, it would be better to use TPS instead of DK in practice.
The influence of Δ2 on the HMQ results is now discussed. Carlson and Foley (1991) stated that larger Δ2 values are necessary in HMQ when using the data from spherical or quadratic-shaped functions such as test functions 4 and 6, whereas very small Δ2 value are required for rapidly varying or highly oscillatory sampled values. As shown in Figs. 5, 6, 7, HMQ yields better results than the other methods for test function 4, even with relatively large Δ2 values, although this is not necessarily true for test function 6. Several researchers have attempted to find an optimal Δ2 value. The formula of Hardy (1971) yields Δ2 values of 0.011, 0.011, and 0.015, and the Franke (1979) formula yields Δ2 values of 0.026, 0.027, and 0.034 for cases 1, 2, and 3, respectively. However, selecting these values as the optimal Δ2 values is not appropriate when considering the results in Figs. 5, 6, 7. Carlson and Foley (1991) argued that the optimal Δ2 value should be estimated with the values of the sampled data as well as the number and location of data points, and proposed their own method for optimal Δ2 in which the data points and values were scaled to the unit cube and interpolated by applying their formula for an effective Δ2 value, and then the resulting interpolants were scaled back to the original domain. Kansa (1990) and Kansa and Carlson (1992) suggested another method in which various Δ2 values for all data points were assessed rather than a constant. However, some ambiguity still remains with their method since the user should provide a minimum and maximum constraint and Δ2 is not dependent on the sampled values but only on the data points. Nonetheless, it is apparent that when a value in the range of about 0.02 to 0.3 is selected for Δ2, better results than the others can be obtained for all functions, with the exception of test function 4, based on the results of Figs. 5, 6, 7.
Mitášová and Mitáš (1993) reported that a generalized tension parameter φ in CRS adjusts the ratio between the weights of the first- and higher-order derivatives in the smooth seminorm and thus controls the behavior of the resulting surface from a membrane to a thin plate. They also remarked that the value of φ should be determined empirically and can be found within a few trials. However, as shown in Figs. 5, 6, 7, the CRS accuracy varies the most depending on the selected φ value, thereby highlighting the potential difficulty in selecting the appropriate φ value. These test results indicate that a φ value in the range from 10 to 20 is recommended to obtain more stable and accurate CRS results.
As stated above, the results of interpolations may be greatly influenced by the selected parameter value. In addition, the suggested optimal Δ2 and φ ranges in HMQ and CRS, respectively, are limited to the test functions that correspond to the true value in this study, and can also be changed according to the number and distribution of sampled points. Through cross-validation methods, it is possible to find the optimal parameter value that minimizes the error of interpolation. However, this approach may be time-consuming and computationally intensive. Furthermore, the accuracy of the interpolated results for a natural phenomenon, especially time-series data which are complex and difficult to predict, cannot be guaranteed. Therefore, it would be preferable to use interpolation methods with no parameters and a certain degree of guaranteed accuracy, such as TPS and QIN.
Application of Interpolation Methods
Fig. 8 shows an example of the numerical results of flow characteristics in a U-shaped channel. The width of the channel is 1.7 m, and the radius of the center line in a curved section is 4.25 m. The slope of the channel bed is 1.76471 × 10-3. Meshes are roughly composed of quadrilateral elements for which Δx and Δy in straight reaches are 0.34 m and 0.17 m, respectively, and Δr and Δθ in a curved reach are 0.17 m and 4.5°, respectively (here, r and θ represent the cylindrical coordinate system). The total number of nodes and elements is 1551 and 1400, respectively. When numerical modeling was performed with specific boundary conditions for the upstream and downstream ends, a slip condition in the lateral side walls, and a fixed bed condition, longitudinal mean flow velocity and water surface elevation were obtained as shown in Fig. 8. Assuming that the observational data at 61 and 15 points were regularly obtained along the A-A' and B-B' routes in Fig. 8a, respectively, the observational points did not coincide with the nodal points. In this case, it is necessary to apply interpolation methods for comparison of the observed values with the numerical results.
The searching radius of the RDW and ISD was not considered, and a generalized tension parameter φ of 15 in CRS and Δ2 of 0.1 in HMQ was chosen for this application. Fig. 9 shows the interpolated results for channel bed, water surface, and mean velocity. Since the results for CRS, TPS, and HMQ are almost identical, they are represented by CRS dotted lines in Fig. 9a. The mean velocity with the QIN along A-A' shows slight differences from those obtained with CRS, TPS, and HMQ, while the results for channel bed and water surface are almost the same for QIN, CRS, TPS, and HMQ, as shown in Fig. 9a. The CRS, TPS, and HMQ show smoothed curves based on radial basis functions, while QIN shows a slight oscillation in the mean velocity. The RDW and ISD show more oscillatory results than the QIN, as well as underestimated values for the mean velocity compared with the others. On the other hand, the water surface and channel bed results along B-B' using HMQ in Fig. 9b show some oscillations unlike those of QIN, CRS, and TPS, while the interpolated mean velocity is the same for QIN, HMQ, CRS, and TPS. Since the results from the QIN are almost identical to those from CRS and TPS, the results from CRS and TPS are overlapped with the representative solid line for the QIN in Fig. 9b.

Fig. 9.
Interpolated results of bed elevation, water surface elevation, and longitudinal mean flow velocity along (a) section A-A' and (b) section B-B' shown in Fig. 8a.
Comparing the processing speed and results, it is clear that the ISD and RDW are superior in terms of calculation time, but produce inferior results when the searching radius is not considered. The CRS and HMQ with properly selected parameters and TPS are fairly reliable, but they are computationally intensive because the entire matrix must be resolved for each variable. The QIN is as fast as the ISD and RDW, and has reliable accuracy to some extent. Therefore, the QIN is proposed as an alternative to traditional interpolation methods for large data fields that are composed of quadrilateral elements.
Conclusion
Analytical solutions for the inverse mapping of local coordinates in an isoparametric square element corresponding to the global coordinates of arbitrarily given points were proposed in this study. In addition, a method for preliminarily determining whether an arbitrary point is within an element with a rectangle or circumcircles enclosing an element was proposed for fast calculation before the estimation of exact local coordinates. Once it was determined that an arbitrary point was located within the quadrilateral element, the values at a target point were interpolated using shape functions of the finite element method when the evaluated local coordinates were between -1 and +1. The details of this proposed algorithm, the quadrilateral irregular network (QIN), were presented, and interpolation schemes of conventional linear combination methods (TIN, RDW, and ISD) and methods based on radial basis functions (TPS, CRS, DK, and HMQ) were briefly summarized. All of these interpolation methods were applied to six test functions and three mesh types to evaluate their accuracy. The results showed that parameters such as searching radius in RDW, ISD, and DK, as well as Δ2 in HMQ, and tension in CRS have a significant influence on the interpolation results, and that inverse distance methods without consideration of a searching radius produce inferior results compared with the other methods. It is difficult to find the optimal parameter value in practical applications because it greatly depends on sampled values as well as the number and location of data points. Therefore, we cautiously recommend the use of methods such as TPS or QIN in order to avoid ambiguity and minimize the amount of effort required for determining non-physical parameter values, although not all of the known interpolation methods were compared in this study. The accuracy of QIN is guaranteed compared with the other methods and there is no need to determine the optimal parameter values. If an initial mesh is maintained without changes, coordinates ξ and η within an isoparametric element for a target point can be saved and reused in subsequent interpolations. Consequently, the QIN is computationally more efficient than conventional methods that require the interpolation values to be reevaluated using all of the nodal values, even when only one of the nodal values changes.