서 론
산사태는 매년 전 세계적으로 상당한 규모의 인명 및 재산 피해를 유발하고 있다. 통계에 따르면 전 세계적으로 자연재해로 인한 전체 인명피해의 약 17%가 산사태에 의한 피해로 보고되고 있다(Lacasse and Nadim, 2009). 우리나라의 경우 산사태 관련 재해로 인해 매년 평균 20여 명의 인명피해가 발생하며, 이는 자연재해로 인한 연간 인명피해의 약 25%를 차지하는 것으로 알려져 있다. 따라서 이러한 산사태의 발생을 예측하고 산사태 발생으로 인한 인명 및 재산 피해를 줄이기 위한 다양한 연구가 수행되고 있다. 산사태의 예측과 관련된 연구는 주로 산사태의 발생 위치 및 시기를 예측하게 되는데, 분석 시 고려되는 영향인자들과 분석되는 위험성의 예측 수준 그리고 산사태 발생 시 예상되는 피해에 대한 고려 여부 등에 따라 산사태 취약성 분석(landslide susceptibility analysis), 산사태 위험성 분석(landslide hazard analysis), 산사태 리스크 분석(landslide risk analysis) 등으로 구분된다. 산사태 취약성 분석(landslide susceptibility analysis)은 분석대상 현장의 상황과 조건에 기초하여 특정 지역에서 산사태가 발생할 가능성(likelihood)을 예측한다. 즉, 어디에서(where) 산사태가 발생할 것인가를 예측하는 것이다. 반면 산사태 위험성 분석(landslide hazard analysis)은 특정 위치와 시간에 산사태가 발생할 확률(probability)을 예측하는 것으로 산사태가 어디에서(where) 그리고 언제(when) 발생할 것인가를 예측한다. 그리고 산사태 리스크 분석(landslide risk analysis)은 산사태 발생에 의해 영향을 받는 인자들(elements-at-risk)과 민감도(vulnerability) 그리고 산사태 발생의 결과인 피해(consequence)까지 고려한다. 따라서 단순히 산사태 발생 위치에 대한 예측만 가능한 취약성 분석에 비해 산사태 위험성 분석이나 리스크 분석은 산사태 발생 시기 예측 등과 같은 좀 더 정밀한 결과를 획득할 수 있고 산사태 발생에 의한 피해 및 비용을 고려할 수 있기 때문에 이러한 분석에 대한 필요성이 제기되어 왔다. 그러나 산사태 위험성 분석이나 리스크 분석은 산사태 취약성 분석에 비해 상당히 많은 종류의 정보를 필요로 하기 때문에 연구 수행에 많은 제약이 있으며, 따라서 현재 국내외에서 획득 가능한 산사태 관련 자료의 수준을 고려할 때 산사태 발생 위치와 산사태 발생 영향 인자들 사이의 상관성을 주로 분석하는 산사태 취약성 분석이 현재로서는 가장 적절한 수준의 예측 결과물이라 할 수 있다. 산사태 취약성 분석은 지난 수십 년 동안 상당히 많은 양의 연구가 수행되어 왔으며, 정성적 분석기법부터 통계적 분석기법, 머신러닝(machine learning) 분석기법 그리고 물리사면모델(physically based model)을 활용한 분석까지 다양한 분석기법이 활용되어 왔다. 특히, 최근 들어서는 컴퓨팅 능력의 빠른 발전과 함께 이러한 컴퓨팅 능력을 효과적으로 활용할 수 있는 머신러닝 기법과 물리사면모델이 활발히 적용되고 있다. 본 논문에서는 최근 들어 활발하게 활용되고 있는 산사태 취약성 분석기법인 물리사면모델을 활용한 분석기법에 대하여 살펴보고자 한다.
산사태 취약성 분석
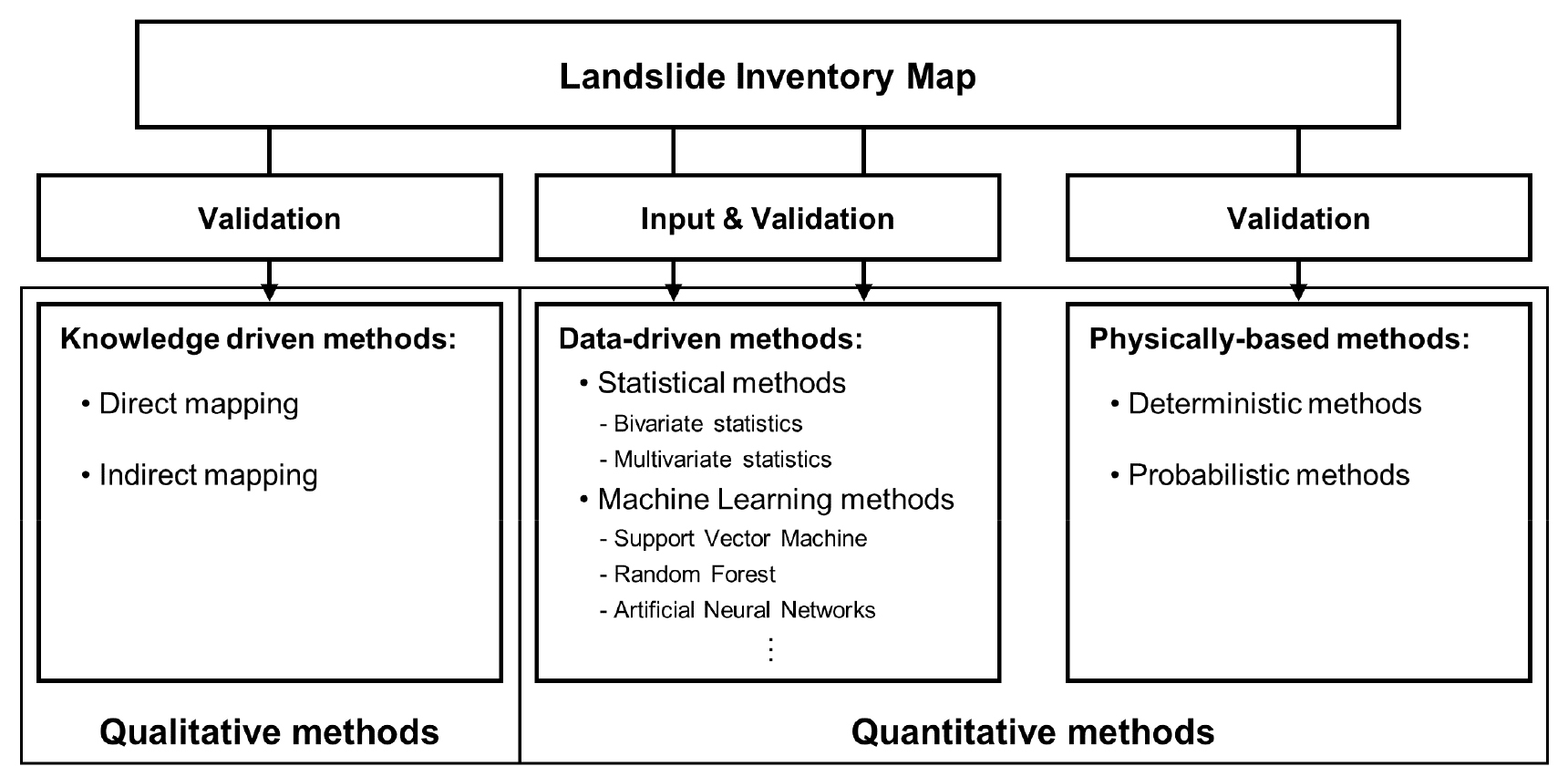
산사태 취약성 분석기법은 산사태 유발 요인과 모델을 다루는 방식에 따라 크게 정성적 분석기법과 정량적 분석기법으로 구분된다(Fig. 1). 정성적 분석기법 중 대표적인 분석기법인 지식 기반 분석기법(knowledge based analysis)은 산사태 취약성을 평가하는 전문가의 판단에 전적으로 의존하는 분석 방식으로(van Westen et al., 1999), 전문가가 현장을 방문하여 평가를 수행하기 때문에 광역적인 지역에 대한 분석에 적합하지 않다(Xie et al., 2004). 반면 정량적 분석기법은 다시 크게 데이터 기반 분석(data-driven analysis)과 물리사면모델 기반의 분석기법(physically based analysis)으로 구분된다. 데이터 기반 분석기법은 과거 산사태가 발생한 위치와 산사태에 영향을 미치는 인자들 사이의 상관성을 분석하여 산사태의 발생 가능성 또는 산사태 발생 예상 위치를 분석하는 것으로, 과거 산사태 발생 이력 자료를 이용하여 각 영향 인자들의 상대적인 중요도를 파악하고 이를 통해 과거 산사태를 유발했던 조건과 비슷한 조건에서 미래에 산사태가 발생할 가능성을 평가한다. 데이터 기반 분석기법은 과거에 통계적 분석기법(statistical analysis)이라고도 불렸으며 최근 들어 좀 더 빠른 알고리즘의 개발과 메모리 및 저장 용량의 급속한 증가 등과 같은 컴퓨팅 기술의 발전으로 인해 불균질하고 불완전한 정보들을 대상으로 분석이 가능하도록 하는 다양한 분석기법들이 제안되고 있다. 특히 지난 20년 동안 머신러닝 및 데이터 마이닝(data mining) 등의 분석기법이 활용되면서 상당한 발전이 이루어지고 있으며, 따라서 산사태 취약성 분석에서도 활발히 적용되고 있다.
정량적 해석기법의 또 다른 분석기법인 물리사면모델 기반의 취약성 분석기법은 산사태 발생 과정을 모사할 수 있는 물리모델을 활용하여 산사태의 발생 과정을 모델링하는 방법이다. 이 방법은 산사태의 기하하적 특성에 따라 사면모델을 결정하고 입력변수인 지질공학적 특성을 고려하여 사면의 안정성을 평가한다. 따라서 데이터 기반의 분석 방법과 달리 산사태 발생 여부와 상관없이 분석을 수행할 수 있으며, 실내 및 현장 실험을 통한 공학적 특성 자료를 획득하여 물리사면모델에 입력자료로 활용하고 계산을 통해 산사태 발생 가능성을 평가한다. 이 방법은 산사태 발생을 유발하는 물리적 프로세스를 재현할 수 있다는 장점으로 인해 활용 가능성이 높은 평가 방법으로 알려져 있다(Fell et al., 2008). 과거 물리사면모델은 단위사면에 대한 안정성 해석에 주로 활용되어 왔으나 최근 들어 지리정보시스템(Geographic Information System, GIS)의 발달로 그리드 기반의 분석이 용이해지면서 광역적인 지역의 산사태 취약성 분석에서 광범위하게 활용되고 있다(Luzi and Pergalani, 1996; Zhou et al., 2003; Xie et al., 2004; Chen et al., 2005; Salciarini et al., 2006; Huang et al., 2007; Godt et al., 2008; Liu and Wu, 2008; Ho et al., 2012; Park et al., 2013). 특히 물리사면 모델은 매우 높은 예측 성능을 보일뿐만 아니라 산사태 발생에 영향을 미치는 개별 인자들에 대한 정량적 평가에 적합한 것으로 알려져 광범위하게 사용되고 있다(Corominas et al., 2014).
물리사면모델
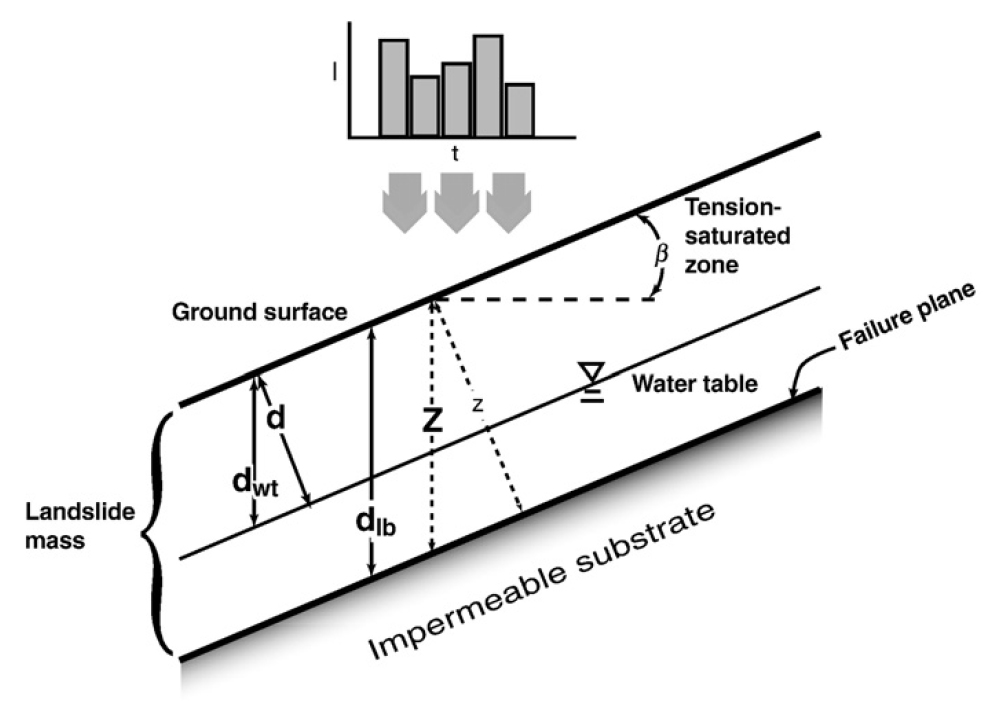
물리사면모델을 활용한 산사태 취약성 분석에서는 무한사면모델(infinite slope model) 등과 같은 물리사면모델을 이용하여 한계평형해석(limit equilibrium analysis)을 수행한다. 한계평형해석은 사면에서 예상되는 파괴면을 따라 미끄러짐을 발생시키려는 힘인 전단응력(shear stress)과 이에 저항하는 힘인 전단강도(shear strength)를 계산하여 이들 사이의 균형을 파악한다. 이때 사용되는 무한사면모델은 예상되는 파괴면이 지반의 표면과 평행하고 예상 파괴면까지의 깊이가 깊지 않은 얕은 깊이의 산사태(shallow landslide)를 모델링하는데 매우 유용한 모델이다. 특히 최근 들어 우리나라뿐만 아니라 전 세계적으로 짧은 시간에 상당히 많은 양의 강우가 쏟아지는 집중강우에 의해 주로 얕은 깊이의 산사태가 발생하고 있기 때문에 많은 연구들이 무한사면모델을 취약성 분석에 활용하고 있다(Kamai, 1991; Terlien, 1996; Pack et al., 1998; Frattini et al., 2004; Huang et al., 2006; Rosso et al., 2006; Godt et al., 2008; D'Amato Avanzi et al., 2009; Apip et al., 2010; Griffiths et al., 2011; Santoso et al., 2011; Ho et al., 2012; Park et al., 2013; Ali et al., 2014; Alvioli et al., 2014; Tsai et al., 2015). 무한사면모델은 그 형태가 단순하기때문에 GIS를 활용한 광범위한 지역의 산사태 분석에 적합한 모델이라 할 수 있다. 무한사면모델을 활용한 안정성 해석은 안전율(Factor of Safety, FS) 산정 공식인 식 (1)을 이용하여 수행된다(Fig. 2).
이때 와 는 각각 사면물질과 물의 단위중량(kN/m3), 와 는 각각 사면물질의 점착력(kN/m2)과 내부 마찰각(degree), 는 사면의 깊이(m), 는 지하수위(m), 는 사면의 경사(degree)이다.
이 식은 사면에서 파괴를 일으키려는 힘, 즉, driving force와 이에 저항하려는 힘, resisting force를 산정하여 이를 비교함으로써 산사태의 안정성을 파악한다. 이 모델에서 간극수압은 유효수직응력을 증가시키고 전단강도를 감소시켜 결과적으로는 사면 파괴를 유발하기 때문에 간극수압의 추정 또는 지하수면의 위치 산정은 산사태 위험성을 평가하는 매우 중요한 요소이다. 그러나 이러한 간극수압이나 지하수면의 위치는 광역적인 지역에서 산정하기 매우 어렵기 때문에 과거에는 고정된 지하수위를 이용하거나 무작위로 지하수위를 추정하여 산사태를 예측하는 연구가 수행되어 왔다(van Westen and Terlien, 1996; Zhou et al., 2003; Xie et al., 2004; Griffiths et al., 2011). 그러나 지하수위는 사면의 경사, 흙의 종류, 강우강도, 그리고 흙의 수리전도도 등에 의해 좌우되기 때문에 이 값을 임의의 고정된 값으로 고려하거나 무작위로 추정하는 것은 부적절하다.
최근의 연구에서는 수리모델을 활용하여 강우의 침투에 의해 발생되는 간극수압의 증가를 계산하고 이를 물리사면모델과 결합하여 간극수압의 상승이 사면의 안정성에 미치는 영향을 분석하는 연구가 진행되고 있다. 즉, 수리모델을 이용하여 강우침투에 의한 지하수위의 높이 또는 간극수압의 증가를 계산한 후 이 값을 이용하여 무한사면모델에서 전단강도의 감소를 계산하고 안전율을 산정하여 산사태의 안정성을 분석하고 있다. 이때 사용되는 수리모델은 크게 정상류 모델(steady state flow model)과 부정류 모델(transient flow model)로 구분된다(Montgomery and Dietrich, 1994; Terlien et al., 1995; Wu and Sidle, 1995; Pack et al., 1998; Baum et al., 2002; Crosta and Frattini, 2003; Savage et al., 2004; Godt et al., 2008). 최근 수년간 수리모델과 물리사면모델을 결합한 다수의 취약성 분석기법이 제안되었으며, 그 중 SHALSTAB(shallow landsliding stability model), SINMAP(stability index mapping), TRIGRS(transient rainfall infiltration and grid based regional slope stability analysis) 등이 가장 널리 사용되고 있다.
정상류 모델
정상류 모델은 강우의 침투가 시간에 따라 변화하지 않고 일정하게 유지되며 포화된 지하수는 사면과 평행하게 흐른다고 가정한다(Montgomery and Dietrich, 1994; Wu and Sidle, 1995). 따라서 하나의 강우 사건에 의한 변화가 아닌 장기간에 걸쳐 발생한 강우 강도와 지하수 흐름의 함수로 지하수위의 공간적 변화를 모사하며 이때 균일한 흐름이 발생한다고 가정한다. 또한 강우강도와 지반의 수리특성 및 지형학적 특성을 고려하기 위하여 다음과 같은 가정을 필요로 한다.
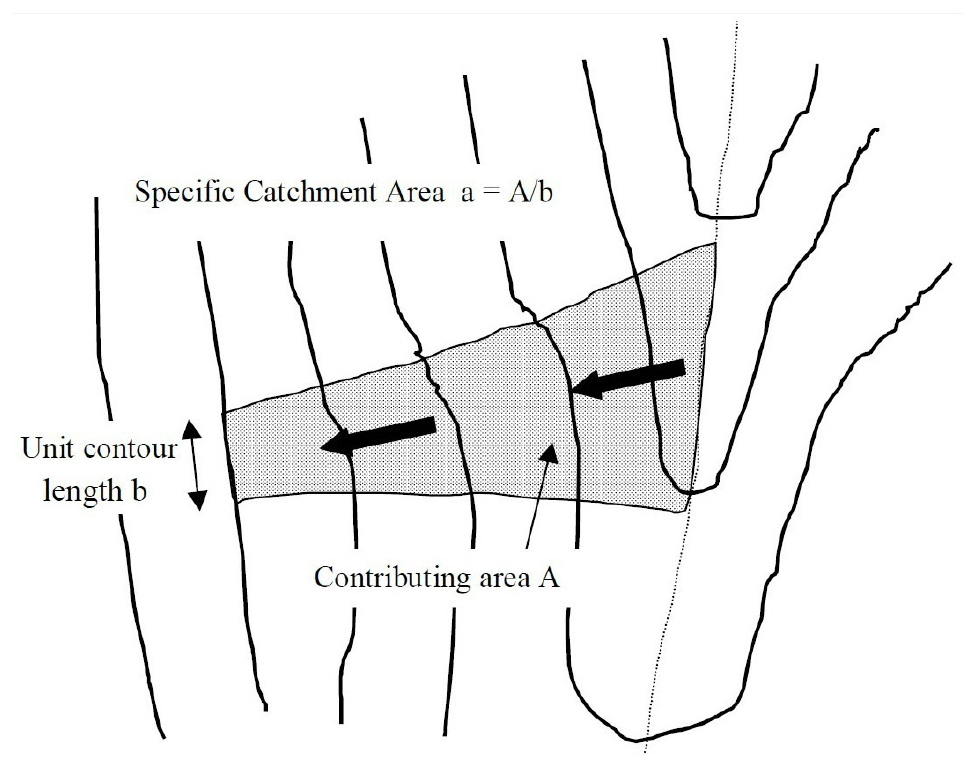
① 강우는 사면의 경사로부터 영향을 받기 때문에 사면의 지형학적 형태로부터 정의된 상부사면의 유역지수를 활용하여 강우에 의한 집수면적을 계산한다(Fig. 3).
② 지하수위는 균일한 강우강도의 영향을 받는 정상 상태에 해당한다.
③ 각 지점에서 지하수 유량은 로 정의한다. 이때 는 지반의 투수계수이고, 이는 수리전도도와 사면의 깊이의 곱으로 나타낸다.
강우에 의한 지하수의 포화정도는 가정 ①과 ②를 기반으로 강우강도와 강우에 의한 집수면적으로 나타내며, 지반의 수리특성 및 배수정도는 가정 ③으로 확인할 수 있다. 이러한 가정을 근거로 정상류 모델의 지하수위는 지반의 깊이에 대한 지하수위의 높이 비율()로 다음 식 (2)와 같이 계산할 수 있다.
이때 은 강우강도(m/h), 는 강우에 의한 집수면적(m2/m), 는 사면의 경사(degree)이다.
이러한 계산식을 이용하여 획득된 지하수위는 안전율의 산정에 활용되며 이러한 분석과정을 통해 광역적인 지역에 대한 안전율 분포를 산정하고 산사태 취약성 지도로 구축할 수 있다. Fig. 4는 앞서 설명된 정상류 모델을 활용하여 광역적인 지역에 대한 안전율의 공간적 분포를 나타낸 강원도 평창 지역의 산사태 취약성 지도 사례이다.
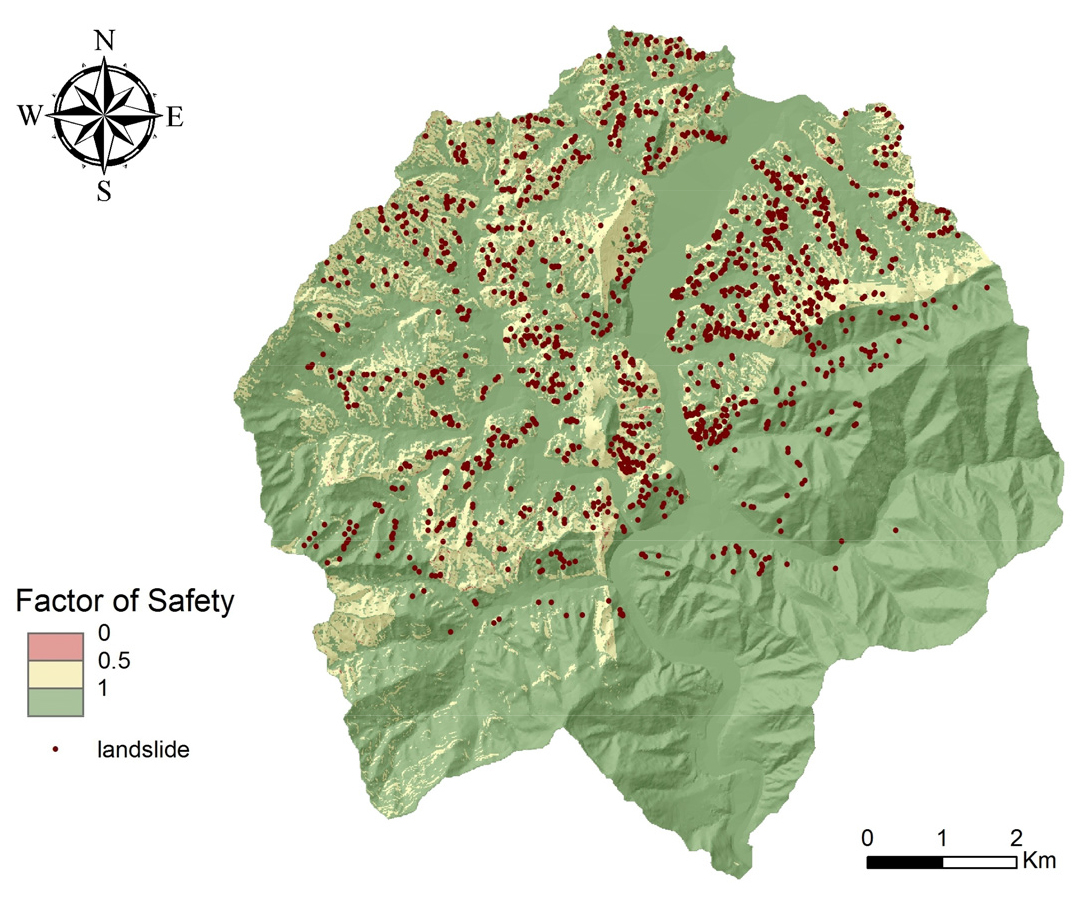
Fig. 4.
Spatial distribution of the factor of safety derived using a physically based model and a steady state hydrological model (Park et al., 2013).
정상류 모델을 기반으로 하는 사면 안정 분석 모델 중 하나인 SHALSTAB은 무한 사면 모델의 방정식에 기초한 안정성 해석 모델과 정상류 수리 모델을 결합한 모델로, 지하수의 흐름이 사면의 기울기와 평행하다고 가정한다(Beven and Kirkby, 1979; O'Loughlin, 1986). 이 모델은 강우 침투가 불투수성의 경계 위에 위치한 사면에 평행하게 흐르는 정상류 상태의 지하수 흐름과 평형상태를 이루고 있다고 가정하고 침투율(infiltration rate)과 기여영역(contributing area)을 고려하여 정상류 흐름을 산정한다. 이때 기여영역은 고려하고자 하는 셀로 유입되는 지하수 흐름을 결정하는 사면 상부의 영역을 의미한다. SHALSTAB은 정상 상태의 간극수압을 계산할 수 있는 간단한 수리학적 모델이기 때문에 많은 연구에서 널리 사용되고 있다(Guimaraes et al., 2003; Fernandes et al., 2004; Gorsevski et al., 2006; Huang and Kao, 2006; Rosso et al., 2006; Sorbino et al., 2010; Listo and Vieira, 2012; Zizioli et al., 2013; Dal Sasso et al., 2014; Pradhan and Kim, 2015; Kim et al., 2016).
SINMAP은 지형 형태를 기반으로 정상류 수리모델에서 얻은 간극수압을 무한사면모델에 적용한 분석 방법이다(Pack et al., 1998, 2001). SINMAP은 지형, 수문 및 토양 특성으로부터 지반 안정성을 추정하는데, 일반적으로 하한(lower bound)과 상한(upper bound)으로 정의되는 균일 확률 분포(uniform probability distribution)를 이용하여 입력 변수의 불확실성을 정량화한다. 이러한 상한과 하한 사이에서 입력변수는 확률 분포를 따라 무작위로(randomly) 변한다고 가정하며, 이러한 범위에 걸쳐 불확실한 입력변수의 균일 분포(uniform distribution)를 가정함으로써 안정성 지수(stability index, SI)를 산정한다. 이때 안정성 지수는 분석 대상 지역이 안전할 확률을 의미한다.
SINMAP과 SHALSTAB은 모두 단면 폭과 기여 면적의 비율을 고려하기 때문에 얕은 깊이의 산사태가 지형적으로 수렴되는 지역에서 집중적으로 발생할 것으로 예측한다. 유동 경로를 지정하는 방법이나 사면물질의 특성 그리고 불안정한 사면을 파악하는 안전율 산정 결과의 사용법과 같은 세부 사항은 두 프로그램이 다르긴 하지만 사면의 안정성을 평가하는 전반적인 접근 방식은 매우 유사하다(Savage et al., 2004). SINMAP 및 SHALSTAB은 기본 모델의 가정이 적절하게 충족되는 광범위한 영역에 대한 사면안정성의 예비 평가에 유용하게 사용될 수 있다. 그리고 두 모델 모두 일정한 강우량 조건하에서 단순한 정상상태의 수리학적 과정을 고려한다. 따라서 두 모델 모두 광범위한 지역에 분포한 사면의 안정성을 예측하는 데 사용될 수는 있지만 지하수 흐름을 정상 상태로 고려하였기 때문에 사면 안정성에 대한 시간적 예측에 어려움이 발생한다. 또한 정상류 모델은 강우 특성이나 현장 조건 등을 비현실적으로 가정한다는 한계를 가지고 있다(Iverson, 2000).
부정류 모델
앞서 설명된 정상류 모델은 시간에 따른 변화가 없는 강우 침투를 고려하기 때문에 단기간에 발생하는 간극수압의 시간적 변화와 이에 따른 안전율의 시간적 변화를 고려할 수 없다는 한계를 가지고 있다. 이러한 한계를 보완하기 위해 제안된 모델이 부정류 모델로, 부정류 모델은 시간에 따른 강우의 부정류 침투 변화를 고려하여 사면의 지하수위를 산정하는 수리모델이다. Iverson(2000)은 Richards 방정식의 근사값을 이용하여 무한사면모델 내에서 침투과정을 고려하여 정상류 모델의 한계를 극복하려고 시도하였다(Arnone et al., 2011). 초기 사면 내부의 간극수압이 정상상태라고 가정하여 강우가 내리는 동안 사면 내부의 간극수압(pore water pressure)을 계산하는데, 강우 발생에 따른 순간적인 압력의 변화를 고려하여 시간의 흐름에 따른 강우강도의 변화와 지반의 공학적 특성을 고려하여 지하수위를 산정한다.
부정류 모델에서 사용하는 강우의 침투 모델은 기본적으로 정상 성분과 침투 성분으로 구성된다. 정상 성분은 정상 침투 속도와 사면의 경사에 의해 결정되는 임의 방향의 흐름을 따르며 비정상 성분은 지표면으로부터 시간에 따라 변화하는 강우의 흐름을 가정한다. 이러한 조건에서 시간의 변화와 지반의 깊이에 따른 간극수압의 순간적인 압력 변화를 예측하기 위해 초기 간극수압 분포(initial pressure distribution)와 강우 자료에 대한 반응 함수(response function)를 고려하여 비정상 간극수압 분포(transient pressure distribution)를 계산한다. 즉 강우강도와 발생 기간, 지반의 확산계수를 고려하여 시간에 따른 지하수의 간극수압을 계산한다(Fig. 5). 이러한 과정을 통해 제안된 부정류 모델은 Richards 방정식(Iverson, 2000; Baum et al., 2002)의 선형 솔루션을 이용하여 부정류 침투해석을 수행할 수 있기 때문에 좀 더 현실에 가까운 해석 결과를 제공할 수 있다. 그러나 부정류 수리모델은 모델의 계산과정에 상당히 다양하고 많은 양의 정보를 요구한다는 어려움이 있다.
부정류 모델을 사용한 사면 안정 분석 모델 중 대표적인 모델인 TRIGRS는 강우침투에 의해 발생하는 간극수압의 시간에 따른 변화를 산사태 취약성 분석에 고려할 수 있다. 즉, TRIGRS는 시간에 따른 강우량 변화를 고려하여 사면 내에서 변화하는 공극수압을 1차원 해석을 통해 획득하고 이를 무한사면모델과 결합하여 해석한다. 이때 강우침투를 모사하는 모델은 Richard의 해석식에 대한 Iverson의 해법에 기초하고 있으며 이를 통해 수리학적 과정이 산사태 발생의 위치와 시간에 어떻게 영향을 미치는지 파악 가능하다. Baum et al.(2002)은 이 식을 일반화하여 TRIGRS 프로그램을 제안하였으며, 이 프로그램은 상당히 많은 연구에서 산사태 발생의 시간적 및 공간적 예측에 범용적으로 사용되고 있다(Baum et al., 2005; Salciarini et al., 2006; Sorbino et al., 2007; Godt et al., 2008; Vieira et al., 2018; Liao et al., 2011; Zizioli et al., 2013; Raia et al., 2014; Bordoni et al., 2015; Lee and Park, 2016). Fig. 6에서 확인할 수 있듯이 부정류 모델을 활용한 경우 시간에 따른 강우량 변화와 함께 안전율의 변화가 발생하고 있음을 확인할 수 있다.

Fig. 6.
Spatial distribution of the factor of safety derived using physically based model and transient hydrological model after (a) 20 mm rainfall of July 11th 2006 and (b) 160 mm rainfall of July 15th 2006 (Lee and Park, 2016).
부정류 모델은 시간에 따라 변화하는 강우량의 부정류 조건을 고려할 수 있기 때문에 산사태 취약성 분석의 해석 능력 향상에 상당히 큰 기여를 하였지만 많은 양의 정밀한 자료를 필요로 한다는 한계를 가지고 있다. 더욱이 흙의 수리특성, 초기 지하수 조건, 그리고 파괴 심도 등과 같이 현장으로부터 획득하기 어려운 입력 자료들이 분석 결과에 상당한 영향을 미친다는 단점을 가지고 있다.
확률론적 해석
앞 서 논의한 바와 같이 산사태 취약성 분석은 정확하고 많은 양의 입력 자료를 필요로 한다. 특히 물리사면모델의 경우 해석에 필요한 입력 자료는 정밀한 DEM으로부터 획득 가능한 지형학적 자료와 현장 또는 실내 실험을 통해 획득가능한 지질공학적 특성 자료로 구분되며 그 중 특히 지질공학적 특성 자료에는 상당한 불확실성이 개입된다. 지질공학적 특성내 불확실성은 자연적인 생성과정을 통해 형성된 지반이 공간적 변동성과 불균질성이 크기 때문이며 광범위한 지역을 대상으로 지질공학적 특성을 파악하기에는 시료의 수가 제한적이라는 점과 맞물리며 불확실성이 개입하게 된다. 따라서 이러한 불확실성은 물리사면모델을 이용한 취약성 분석에 필연적으로 개입하게 되며 불확실성은 예측 모델을 이용하여 분석한 산사태 취약성 분석 결과의 정확도에 영향을 미치고 오류를 발생시키는 원인이 된다. 결국 물리사면모델을 활용하여 산사태 취약성 분석을 수행하는 경우 정밀한 예측을 위해서는 불확실성이 반드시 고려되어야 한다. 그러나 물리사면모델을 활용한 기존의 연구들은 입력변수 내 불확실성에 대한 고려없이 입력 변수의 평균값만을 사용한 결정론적 해석기법을 적용하여 광역적인 산사태 취약성 분석을 수행하였다. 결정론적 해석기법은 불확실성이 포함된 입력변수를 고정된 하나의 값으로 분석을 수행하기 때문에 입력 변수 내 불확실성을 고려하기 어렵다. 이러한 불확실성은 확률론적 해석(probabilistic analysis)을 적용하여 정량적으로 분석되어 왔으며 따라서 산사태 취약성 분석에서도 확률론적 해석은 불확실성을 다루는 효율적인 도구로 활용될 수 있다.
일반적으로 확률론적 분석에서는 무한사면모델에서 사용되는 입력변수들의 불확실성을 고려하기 위해 입력변수를 확률변수(random variable)로 고려한다. 그 중 특히 마찰각이나 점착력 같은 강도정수의 경우 그 특성을 파악하기 힘들기 때문에 불확실성이 개입될 가능성이 높으며 따라서 많은 연구에서 확률변수로 고려되었다. 확률론적 해석을 위해서는 확률변수의 통계 매개변수(즉, 평균 및 표준 편차)와 확률 밀도 함수(probability density function, PDF)를 결정해야 하며, 획득된 확률변수의 통계 매개변수 및 확률밀도함수 그리고 물리사면모델을 이용하여 확률 분석을 수행한다. 가장 일반적으로 사용되는 확률론적 분석 방법에는 1계 2차 모멘트 방법(First Order Second Moment Method, FOSM), 점추정법(Point Estimate Method, PEM) 및 몬테카를로 시뮬레이션(Monte Carlo simulation, MCS) 등 있다. 이 중 FOSM과 PEM은 확률변수에 대한 추가적인 정보가 부족한 경우에도 평균과 표준편차만을 이용하여 파괴확률을 대략적으로 추정할 수 있다는 장점이 있으나 성능 함수가 복잡해지면 계산이 불가능해지는 한계를 가지고 있다. 더욱이 이들 방법은 파괴확률에 대한 근사값을 구하는 데에만 사용할 수 있기 때문에 확률변수로 고려되어야 하는 안전율의 분포 등을 결정하는 데 한계를 보인다(Harr, 1987; Park and West, 2001). 반면 MCS는 가장 널리 사용되는 확률론적 분석 방법 중 하나로, 원칙적으로는 결정론적 분석이 가능한 모든 모델에 적용할 수 있다는 장점을 가진다. 또한 MCS는 확률변수의 PDF를 파괴확률 산정에 이용하며 반복계산을 통해 안전율의 PDF를 획득할 수 있기 때문에 가장 완벽한 확률론적 분석방법이라고 할 수 있다(Park et al., 2013). 한편 과거에 비해 컴퓨팅 성능이 빠른 속도로 발전함에 따라 반복적인 계산이 훨씬 용이하게 수행될 수 있으며, 프로그래밍을 통해 상대적으로 용이하게 다양한 형태의 함수들을 활용할 수 있다는 장점을 가지고 있다(Baecher and Christian, 2003). 확률론적 해석에 대한 자세한 설명은 여러 문헌에서 제공되고 있으므로 자세한 설명은 참고문헌을 통해 확인할 수 있다(Harr, 1987; Baecher and Christian, 2003; Chowdhury et al., 2010). 이러한 여러 장점으로 인해 확률론적 해석기법과 물리사면모델을 이용한 산사태 취약성 연구는 다양한 연구에서 활용되고 있으며 특히 GIS의 활용을 통해 광역적 지역에 대한 확률론적 해석기법 기반의 산사태 취약성 분석이 가능하게 되었다(Zhou et al., 2003; Shou and Chen, 2005; Meisina and Scarabelli, 2007; Shou et al., 2009; Terhorst and Kreja, 2009; Yilmaz and Keskin, 2009; Park et al., 2013, 2019; Rossi et al., 2013; Raia et al., 2014; Lee and Park, 2016; Salciarini et al., 2017; Marin and Mattos, 2020). 확률론적 해석과 물리사면모델을 결합한 산사태 취약성 분석 결과는 Fig. 7과 같이 산사태의 발생 가능성에 대한 확률(probability of failure) 또는 spatial probability of landslide occurrence로 표시할 수 있다.

Fig. 7.
Spatial distribution of failure probability derived using a physically based model and probabilistic approach (Lee and Park, 2016).
결 론
본 논문은 산사태 취약성 기법의 종류 및 장단점에 대하여 논의하고 최신 연구 경향, 특히 물리사면모델을 활용한 산사태 취약성 분석 기법의 최근 연구에 대하여 논의하였다. 산사태 취약성 연구는 크게 정성적 기법과 정량적 기법으로 구분되며 정량적 기법은 다시 데이터 기반 분석과 물리사면모델 기반의 분석으로 구분된다. 물리사면모델을 활용한 산사태 취약성 분석은 높은 예측성능과 산사태의 발생 프로세스를 재현할 수 있다는 장점으로 인해 최근 활발히 활용되고 있다. 특히 데이터 기반의 취약성 분석기법들과 달리 물리사면모델을 활용한 분석기법은 산사태 발생 이력의 존재 여부와 상관없이 취약성 분석이 가능하고 공학적인 요인들을 분석에 활용가능하다는 점으로 인해 다른 분석기법에 비해 향후 활용가능성이 높은 분석기법으로 인정되고 있다. 분석에 활용되는 사면모델은 다양한 모델이 적용될 수 있으나 최근 집중강우에 의해 발생되는 산사태의 형태가 주로 얕은 깊이의 산사태라는 점을 고려하여 무한사면모델이 주로 활용되고 있다. 특히 최근 들어 GIS의 발달과 더불어 그리드 기반의 분석이 가능해짐에 따라 광역적 지역에 대한 분석에서의 활용도가 더욱 증가하고 있다. 또한, 해석의 중요한 입력 인자인 지하수위의 경우 강우의 침투모델에 기반한 수리모델을 결합하여 강우량에 따른 지하수위 변화를 산정하고 이를 활용하여 분석을 수행하고 있다. 물리사면모델과 결합하여 분석에 활용되는 수리 모델에는 강우 침투가 시간에 따라 변화하지 않고 일정하게 유지된다고 가정하는 정상류 모델과 시간에 따른 강우의 침투 변화를 고려하는 부정류 모델이 있으며 현장의 강우조건에 따라 두 모델 모두 활용되고 있다. 한편 이전 연구에 따르면 물리사면모델에 활용되는 입력 인자들의 경우 광역적인 지역으로부터 획득하기 어렵다는 점 때문에 유역 단위의 소규모 지역에 대한 분석에 주로 활용하도록 제안되어 왔다. 그러나 확률론적 해석기법의 적용과 함께 입력 인자들 내에 내재되어 있는 불확실성을 효율적으로 정량화할 수 있게 됨에 따라 이러한 문제점들도 보완되고 있어 향후 좀 더 많은 연구에서 활용될 수 있을 것으로 판단된다.