서 론

수직 수리전도도(Kv)는 지표수와 주변 대수층 간의 물 및 물질 교환에 영향을 결정짓는 중요한 변수로, 이를 정확히 측정하는 것은 지표수와 지하수 시스템 간 상호작용을 이해하는 데 필수적이다(Storey et al., 2003; Saenger et al., 2005; Genereux et al., 2008; Abimbola et al., 2020). 하상 퇴적물의 Kv를 측정하기 위해 다양한 방법이 활용되고 있으며, 그중 대표적인 것이 현장 변수두 투수시험(field falling-head permeameter test)(Chen, 2000; Landon et al., 2001; Genereux et al., 2008), 정수두 주입시험(constant head injection test)(Cardenas et al., 2004), 순간충격시험(slug test)(Cey et al., 1998), 입도 분석(grain size analysis)(Alayamani and Sen, 1993) 그리고 piezo-seep meter(Kelly and Murdoch, 2003) 등이 있다.

이 중 현장 변수두 투수시험은 간단한 장비와 짧은 시간으로 측정할 수 있어 효율적이다. 양단이 개방된 원통형의 파이프인 퍼미아미터(permeameter)를 시험 대상 퇴적층에 수직으로 삽입한 후, 목표 수위까지 파이프에 물을 채우고 경과시간에 따른 퍼미아미터 내 퇴적물 상부의 수위 변화를 분석하여 Kv [L/T]를 산출한다. 식 (1)의 Hvorslev equation(Hvorslev, 1951)을 이용하는 Chen(2000)과 Genereux et al.(2008)의 방법이 이러한 접근 방식에 널리 활용되고 있다.

여기서, D [L]는 퍼미아미터의 직경, Lv [L]는 퍼미아미터 내의 퇴적물(sediment column)의 수직 길이, h1 [L], h2 [L]는 시험 시작 후 경과시간 t1[T], t2[T]에서의 수위이다. m은 수평 수리전도도와 Kv 비의 제곱근이다.

Chen(2000) 방법은 식 (1)에서 πD11m항을 생략한 식 (2)를 Kv 결정에 이용한다(Chen, 2004). 식 (2)에서 h [L]는 지표수위를 기준한 퍼미아미터 내 퇴적물 상단부의 수위로서, 수위 경과시간과 수위변화 간의 상관관계로부터 통해 Kv를 구한다.

반면, Genereux et al.(2008) 방법은 Hvorslev equation(Hvorslev, 1951)을 변형한 식 (3)을 사용한다. 식 (3)에는 수평 수리전도도와 Kv 비의 제곱근인 미지의 값 m이 포함되어 있어, Kv를 계산하기 위해서는 m에 대한 정보 또는 전제가 요구된다. Genereux et al.(2008) 방법에서는 m값을 1과 ∞로 하여 산출된 각 각의 Kv를 평균하여 퍼미아미터 내 퇴적물의 Kv로 정하였다. 또한 Chen(2000) 방법과는 달리 시험 전의 퍼미아미터 내 안정수위(initial water level, IWL)를 기준으로 퍼미아미터 내 수위 변화를 측정한다. 두 방법 모두 수리구배를 직접 고려하지 않고, 퍼미아미터 내 퇴적물 상부 수위 변화만 측정한다는 공통점이 있다.

Lee(2024)는 Chen(2000)과 Genereux et al.(2008) 방법과는 달리, 시험 시작 이후 경과시간에 따른 퍼미아미터 내 퇴적물 상, 하단부 수위 변화를 모두 측정하고, 이로부터 구한 시험 경과시간별 통과 유량과 수리구배 값을 Darcy equation으로부터 유도된 식 (4)에 적용하여 Kv를 산출하는 방법을 제안하였다.

여기서, As [L²]와 Af [L²]는 퍼미아미터 내 퇴적물과 수위 측정용 튜브의 단면적이다. H [L]와 h [L]는 퍼미아미터 내 퇴적물 상단부와 하단부의 수위이며, ΔHh [L]는 H와 h간의 수위 차이다.

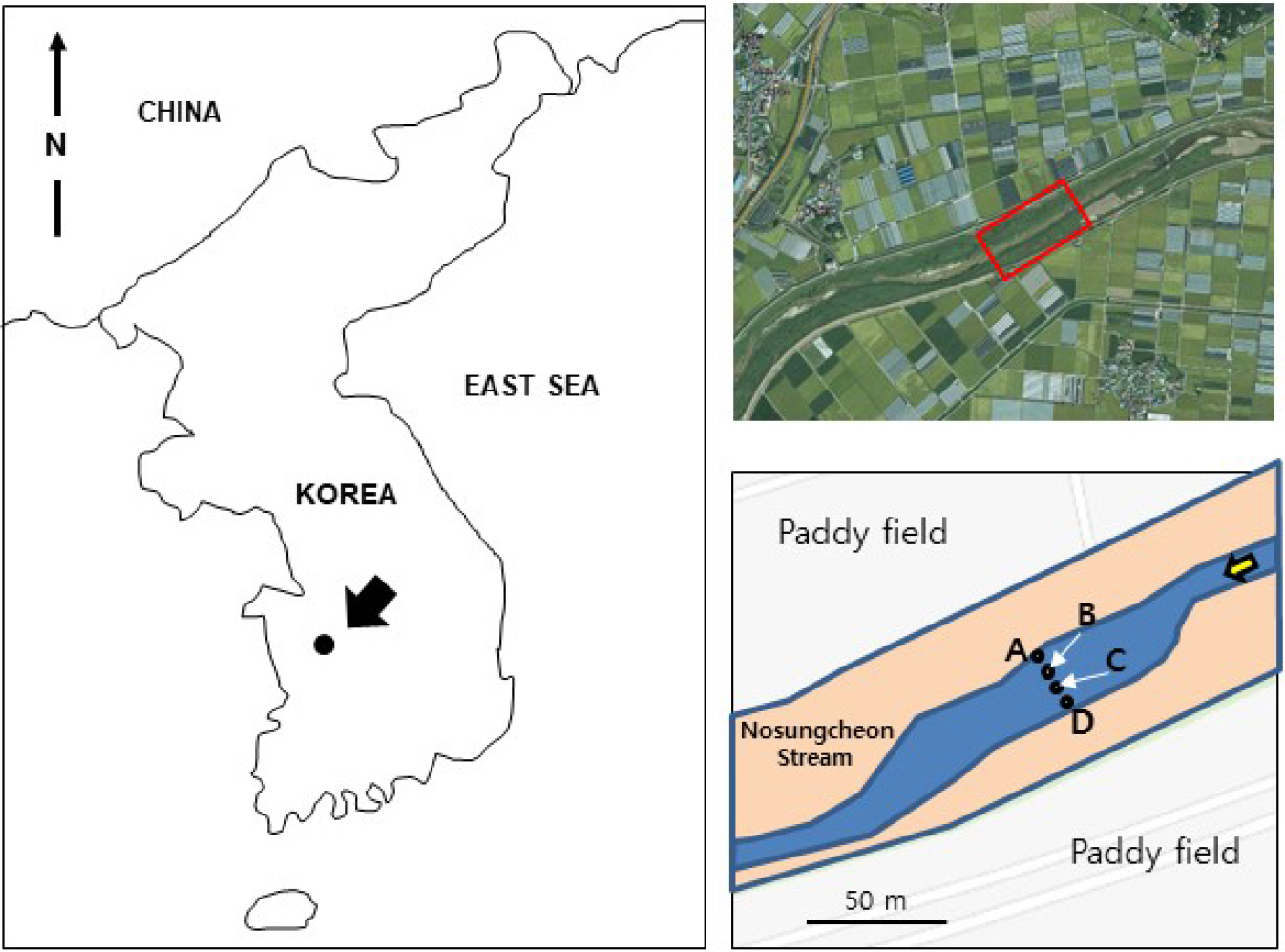
본 연구는 하상 퇴적물의 Kv를 산출하는 데 있어 Chen(2000), Genereux et al.(2008), Lee(2024)의 세 방법의 특성과 장, 단점을 비교하는데 목적이 있다. 이를 위해 현장 시험과 모래수조(sand tank)와 정수위조(constant-head reservoir)를 활용한 실내 시험을 수행하였다. 실내 시험은 인위적으로 손실(losing) 및 이득(gaining) 조건을 모사하기 위해 모래수조와 정수위조 간의 수위 차를 조절하고, 동일 조건하에서 세 가지 방법을 적용하여 도출된 Kv를 비교 ‧ 분석하였다. 현장 시험은 논산시 광석면을 통과하는 노성천의 4개 지점 하상 퇴적물에 수직으로 삽입한 퍼미아미터를 이용하여 수행하였다. 각 지점별로 세 방법을 적용하여 Kv를 산출하고, 이를 비교하였다.

재료 및 방법

실내 시험

시험에 이용된 모래수조는 직경 63.5 cm, 높이 80 cm의 스테인리스 스틸 재질로 제작된 원형의 통이다(Fig. 1). 모래수조 상단부에는 유출구를 설치해 수위를 일정하게 유지하였으며, 정수위조와 연결하기 위해 모래수조와 정수위조 바닥에도 유입 ‧ 출입구를 마련하였다. 두께 40 cm의 모래층의 포화상태를 포화, 유지하기 위해 시험 시작 전에 정수위조에서 모래수조로 물을 수일 동안 지속적으로 공급하였다.

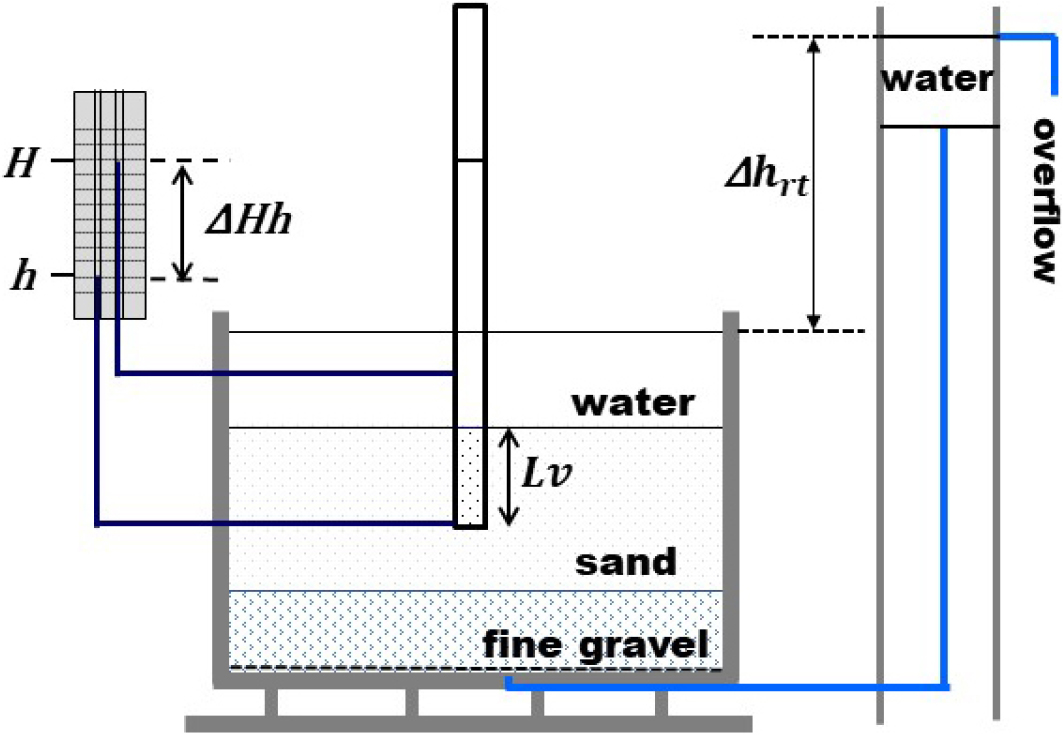
Fig. 1.

Experimental setup for laboratory falling-head permeameter tests to determine Kv. ① Water level scale, ② overflow sand tank, ③ permeameter standpipe, ④ constant-head reservoir, and ⑤ water hose. Lv and Δhrt represent the length of the sediment column within the permeameter, and the difference in water level between the sand tank and the constant-head reservoir, respectively.

모래층 35 cm 깊이에 수직으로 설치한 퍼미아미터는 직경 6.3 cm, 길이 1.2 m, 두께 1 mm의 스테인리스 스틸 파이프이다. 퍼미아미터 설치 심도는 퍼미아미터 직경에 대한 퍼미아미터 설치 깊이의 비(L_v/D)가 5 이상일 때 측정 수리전도도의 정확도가 향상된다(Chen, 2004; Genereux et al., 2008; Burnette et al., 2016)는 점을 고려하여 결정하였다.

퍼미아미터의 하단부와 중간부에 수위 측정용 튜브를 연결하기 위한 연결구가 설치되어 있다. Chen(2000)과 Genereux et al.(2008) 방법에 따른 변수두 투수시험에서는 중간부 튜브를 개방하여 퍼미아미터 내 퇴적물 상부 수위를 측정하였고, Lee(2024) 방법에서는 중간부와 하단부의 튜브를 개방하여 각각의 수위를 측정하였다. 중간부 연결구는 모래층 바로 위 물 속에 위치하도록 하였다. 모래수조 내 손실(losing) 및 이득(gaining) 조건의 물 흐름을 모사하기 위해, 모래수조와 정수위조 간의 수위 차이(Δhrt)를 조절하였다. 정수위조의 수위가 모래수조보다 높을 경우, 모래수조 내 물의 흐름은 상 방향을 형성한다. 반대로, 정수위조의 수위가 모래수조보다 낮을 경우에는 하 방향의 물 흐름이 유도된다. 이러한 설정은 다양한 유동 조건에서 Chen(2000), Genereux et al.(2008), Lee(2024) 방법을 각각 적용하여 변수두 투수시험을 실시하고, 각 방법으로 산출된 Kv를 비교 ‧ 분석하기 위해 이루어졌다.

실내 시험에서는 가장 먼저 모래수조와 정수위조 간의 수위 차(Δhrt)를 조정 후 고정하고, 퍼미아미터 내 퇴적물 상부 수위가 안정될 때까지 기다렸다. 퇴적물 상부 수위의 안정 여부는 상부 수위 측정용 튜브 내의 수위의 변화 여부로 확인하였다. 모래수조 수위와 퇴적물 상부의 안정수위를 측정한 다음, 퍼미아미터 내로 물을 공급하였다. 이 때, 물 공급은 퍼미아미터 내부의 퇴적물이 교란되지 않게 퍼미아미터 파이프 벽을 타고 물이 조금씩 흘러내리도록 조절하였다. 목표 수위인 퍼미아미터 상단부 끝에서 물이 넘쳐흐르게 공급하면서 퍼미아미터 하단부의 수위 안정 여부를 확인하였다. 퍼미아미터 내 퇴적물 상, 하단부의 안정수위를 측정한 후, 퍼미아미터로의 물 공급을 중단하여 시험을 시작하였다. 시험 경과시간별로 퍼미아미터 내 퇴적물 상, 하단부 수위를 측정하였으며, 퇴적물 상부의 수위가 시험 전 안정수위에 근접하면 시험을 종료하였다. 가능한 다양한 이득 및 손실환경에서의 시험 결과를 도출하기 위해 실험 조건이 허용되는 범위 내에서 Δhrt를 46.0, 31.9, 16.9, 0.0, -11.9, -24.9, -37.0 cm의 7단계로 하여 시험을 진행하였다. 각 단계별로 시험을 3회씩 반복하였다.

현장 시험

현장 시험은 충남 논산시 광석면을 동쪽에서 서쪽으로 흘러 금강에 합류되는 노성천의 하상퇴적물을 대상으로 수행하였다(Fig. 2). 하상퇴적물의 입도는 조립질 모래 내지 세립질 자갈로 이루어져 있다. 시험 당시 하천의 유로 폭은 약 25 m, 평균 수심은 약 40 cm 이었다. 스테인리스 스틸 재질의 퍼미아미터(길이 1.5 m, 직경 6.3 cm, 두께 1 mm) 4개를 유로 방향과 직각으로 2 m 간격으로 설치하였으며, 퍼미아미터 직경에 대한 퍼미아미터 설치 깊이의 비(L_v/D)가 5 이상이 되도록 55 cm (Point A), 44 cm (Point B), 49 cm (Point C), 50 cm (Point D) 깊이에 퍼미아미터를 수직으로 삽입하여 설치하였다. 시험 전 각 퍼미아미터 내 초기 안정수위와 지표수위의 차이는 1 mm 안팎이었으며 육안으로 그 차이를 측정하기 어려워 하천수위는 별도 측정하지 않았다. 퍼미아미터 설치 후, 퍼미아미터 내 수위가 안정된 후 시험을 진행하였다. 퍼미아미터 내 안정수위를 기준으로 퇴적물 상부 수위를 측정하였다. 각 지점별로 동일 시험을 5회씩 반복하였다.

Fig. 2.

Location map of the field test site. Four permeameters were vertically inserted into the streambed sediments at depth of 55 cm (Point A), 44 cm (Point B), 49 cm (Point C) and 50 cm (Point D).

결과 및 토의

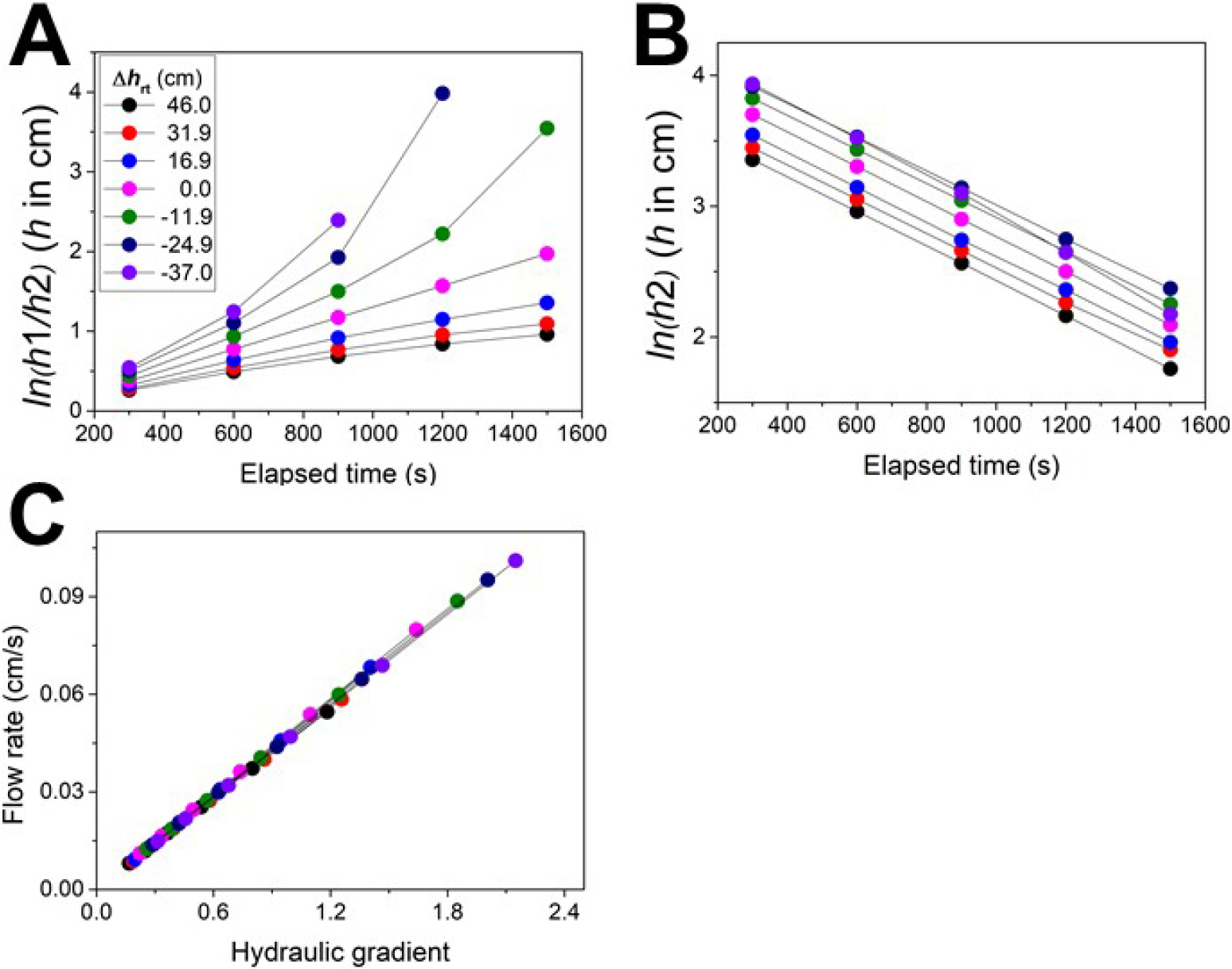
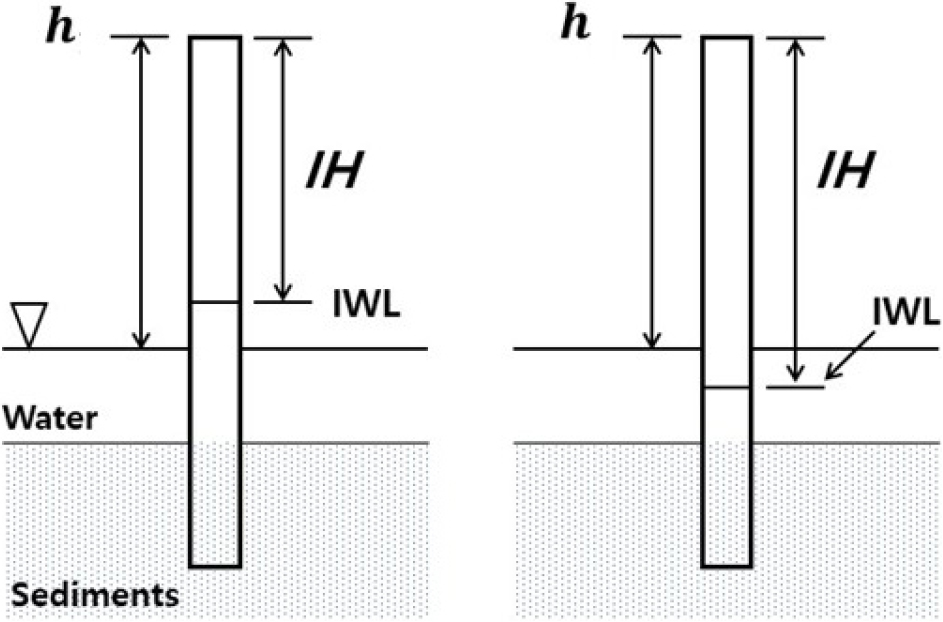
실내 시험에서 수집된 모래수조 수위, 안정수위(IWL), 그리고 각 분석 방법에 따른 수위 측정 자료는 Table 1과 같다. 시험 시작전의 초기수위(h1)는 퍼미아미터 최 상단부 끝의 높이이며, Chen(2000) 방법에 적용하는 수위는 모래수조 수위 기준, Genereux et al.(2008) 방법에 적용하는 수위는 퍼미아미터 내 퇴적물 상단부의 안정수위 기준으로 측정하였다(Fig. 3). Kv 결정은 Chen(2000)의 경우, 식 (1)과 같이 경과시간과 퍼미아미터 내 퇴적물 상단부의 수위변화(ln(h1/h2)) 간, Genereux et al.(2008)은 경과시간과 퍼미아미터 내 퇴적물 상단부의 수위변화(ln(h2)) 간의 직선 회귀식의 기울기로부터 이뤄진다. Lee(2024) 방법에서도 수리구배와 통과 유량간의 직선 회귀식의 기울기로부터 수리전도도가 결정되므로, 세 방법에 의한 수리전도도 결정의 정확도와 신뢰도 평가를 위해서 퇴적물 상단부 수위변화와 경과시간 간, 그리고 수리구배와 통과 유량 간 선형 회귀분석을 통한 선형성(linearity) 평가가 요구된다(Table 2).

Fig. 3.

Results of laboratory falling-head permeameter tests. A: ln(h1/h2) vs elapsed time diagram based on the Chen method. B: ln(h2) vs elapsed time diagram based on the method of Genereux. C: Flow rate vs hydraulic gradient diagram based on the Lee method.

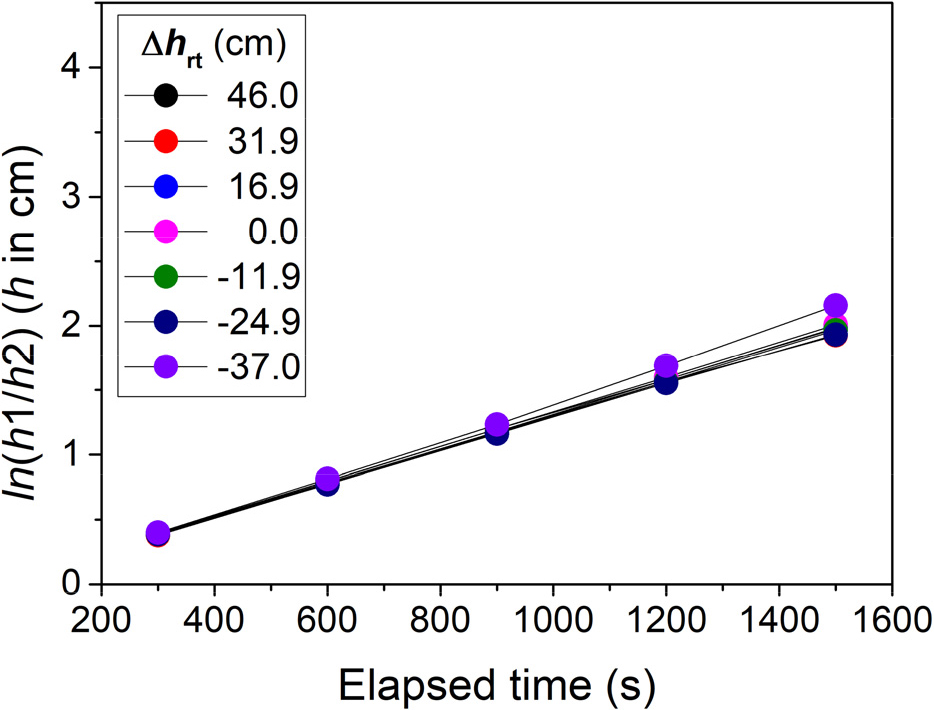
Fig. 3A는 Chen(2000) 방법으로 측정된 퇴적물 상부 수위 변화와 경과시간 간의 관계를 나타낸다. 모래수조와 정수위조의 수위가 같을 때, 즉 Δhrt = 0.0 cm 일 때 경과시간과 ln(h1/h2) 간 상관관계가 가장 높다(R² = 0.999, p-value = 3.1E-8)(Table 2). 그러나 정수위조와 모래수조간의 수위 차(Δhrt)가 커질수록 직선 관계에서 벗어나는 경향을 보이며, 이득 환경보다 손실 환경에서 이러한 경향이 두드러진다. 실제 Δhrt = -37.0 cm 일 때의 R²값(0.962)은 p 값이 0.05 초과로 나타나 선형 회귀분석 결과의 유의성이 떨어지며, ln(h1/h2)와 경과시간 간의 관계 역시 비선형임이 확인된다. Δhrt가 -24.9 cm와 -37.0 cm인 단계에서는 음의 h 측정값이 확인되는데, 이는 시험 후반부의 퍼미아미터 내 수위가 모래수조의 수위 보다 낮아졌기 때문이다. 음의 h 측정값에 대한 자연 로그 값를 얻지 못하므로 해당 측정값은 Kv 결정을 위한 자료 분석에 이용할 수 없다. Chen(2000) 방법을 이용한 Kv 결정에 있어서의 문제점은 모래수조 수위 기준의 수위가 변수두 투수시험 동안 퍼미아미터 내 퇴적물 상단부에 실제 가해지는 가압수두(imposed head, IH)를 반영하지 못하기 때문이다. 즉, 모래수조 수위를 기준한 수위는 이득 환경에서는 가압수두보다 크게, 손실환경에서는 작게 측정되어 수위 측정에 오차가 포함되게 하는 원인이 된다(Fig. 4). Chen(2000) 방법에 안정수위를 기준한 수위를 적용했을 경우, ln(h1/h2)와 경과시간 간 관계는 선형성을 회복하였다(Fig. 5). 모든 Δhrt 단계에서 0.998 이상의 R²를, 0.05 미만의 p 값을 갖는다. 모래수조 수위와 정수위조 수위가 같아 모래수조 내 수직의 물 흐름이 없는 경우에는 퍼미아미터 내 안정수위가 모래수조 수위와 같으므로, 모래수조 수위 기준의 가압수두와 퇴적물 안정수위 기준의 가압 수두는 동일하다.

Fig. 4.

Water levels adopted for the Chen and Genereux methods under gaining (left) and losing (right) conditions. h represents the water levels adopted for the Chen, while IH for the Genereux methods. IH is the imposed head and IWL is the initial water level.

Fig. 5.

ln(h₁/h₂) vs elapsed time diagram based on the Chen method. The water level adopted for the method is referenced to the initial water level inside the permeameter, not to the sand tank water level.

Fig. 3B의 Genereux et al.(2008) 방법을 적용한 결과에서는 경과시간과 퇴적물 상부 수위 변화(ln(h2)) 간 관계는 거의 모든 시험 조건에서 R²가 0.998 이상(p 값이 0.05 미만)의 선형 관계를 보여준다(Table 2). 직선 회귀식의 기울기가 Δhrt가 -37.0 cm인 단계를 제외하면, 최소 0.00129, 최대 0.00134의 범위를 보이며, 이로부터 산출되는 Kv 역시 근소한 차이를 보인다. Δhrt가 -37.0 cm인 단계에서의 기울기는 0.00146이다.

Lee(2024) 방법으로 산정한 통과 유량과 수리구배 간 관계는 모든 시험 조건에서 결정계수 값이 0.999 이상이며, p-value 역시 세 방법 중 가장 낮은 값의 범위를 보인다(Table 2). 7 단계의 시험 자료로부터 구한 통과 유량과 수리구배가 동일 직선상에 중첩되어 나타나는 사실 역시 회귀분석 결과와 부합한다(Fig. 3C). Kv(회귀식의 기울기) 역시 최소 0.0458 cm/s, 최대 0.0488 cm/s로 근소한 차이를 보인다.

Genereux et al.(2008)과 Lee(2024) 방법에 의한 Kv 값들은 모든 Δhrt 단계에서 비교적 일정한 범위의 값들을 보이는 반면에, Chen(2000) 방법에 의한 결과 값들은 모래수조와 정수위조 간의 수위 차(Δhrt)에 크게 영향을 받는 양상을 보인다(Fig. 6A). 이러한 결과는 전술한 바와 같이 모래수조 기준의 수위를 변수두 투수시험 결과 분석에 적용한데 기인하는 것으로 판단되며, 실제 안정수위 기준의 수위를 Chen(2000) 방법에 적용하였을 경우, 모든 Δhrt 단계에서 Genereux et al.(2008)과 Lee(2024) 방법에 의한 결과에 근소한 차이의 Kv 값의 범위를 보인다(Fig. 6B). 실제 세 방법간 차이가 가장 큰 Δhrt = 46.0 cm 단계에서도 Chen(2000)과 Lee(2024) 간, Chen(2000)Genereux et al.(2008) 간의 평균 Kv 값 차이는0.004 cm/s, 0.001 cm/s 이다.

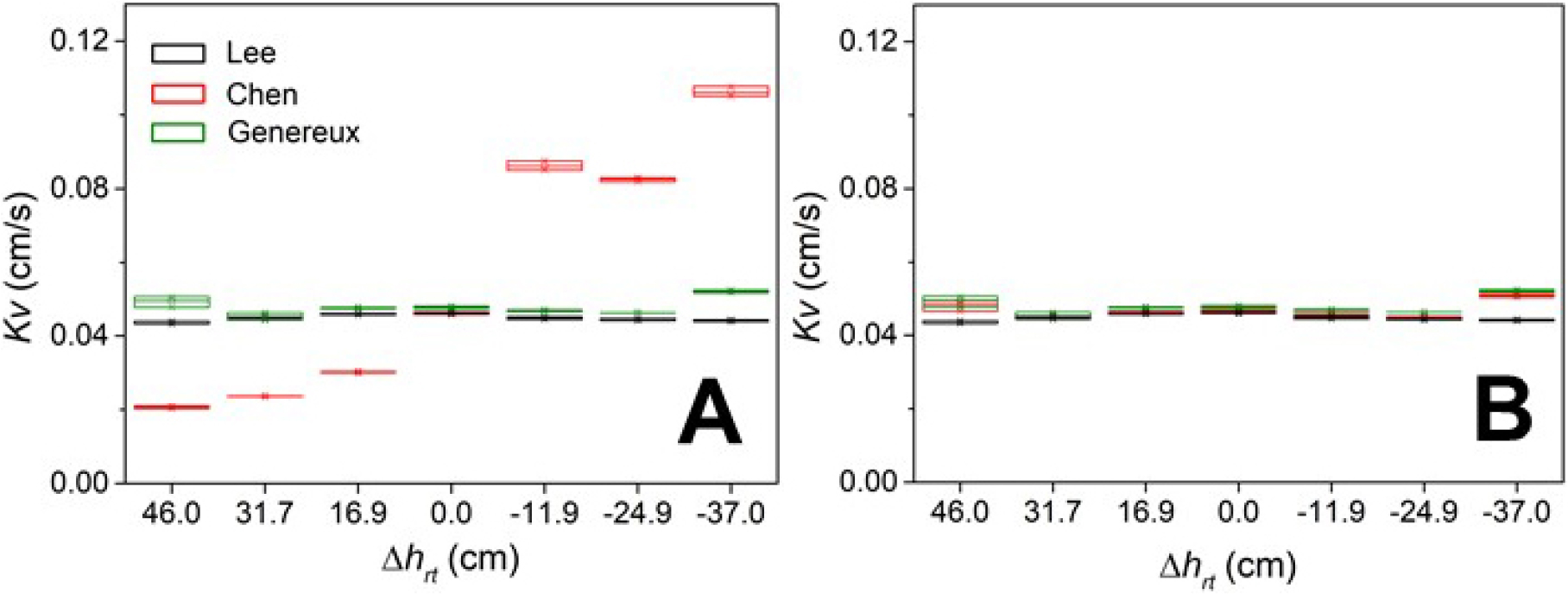
Fig. 6.

Comparison of Kv values determined by the three analytical methods. A: Box plots for Kv values calculated using the Chen, Genereux and Lee methods. B: Box plots for Kv values using the Genereux and Lee methods are identical to those in panel A. However, the Kv values by Chen method in this panel are determined based on water levels measured relative to the initial water level inside the permeameter, not to the water level of the sand tank.

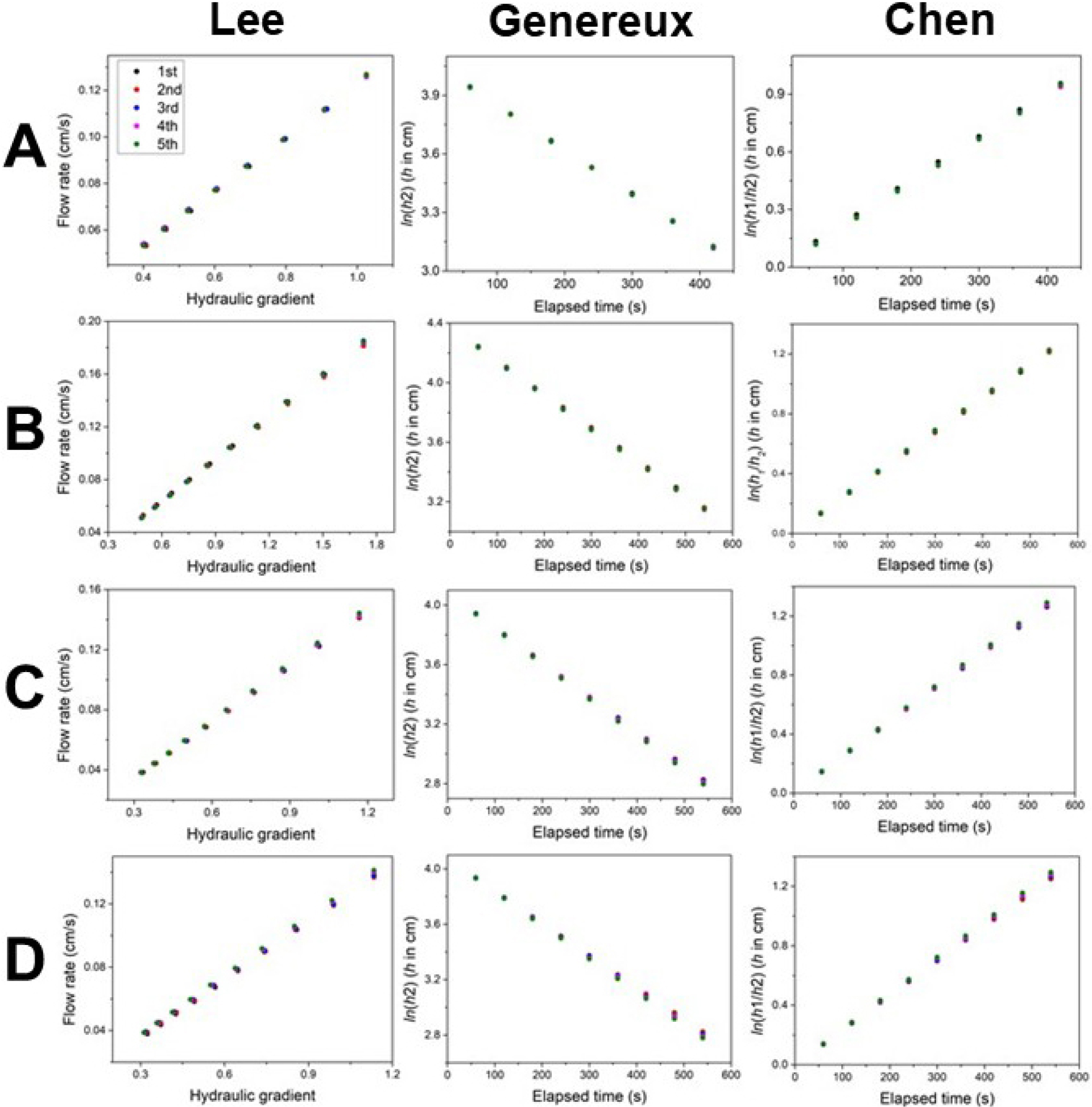
충남 논산 광석면 노성천의 하상퇴적물을 대상으로 한 4개 지점에서의 변수두 투수시험에서 방법별 수위 측정 간격과 시험 소요시간은 공통적으로 1 분과 7 분이었으며, 시험은 동일 조건에서 5 회씩 반복하였다. Fig. 7에서 보는 바와 같이 4개 지점에서 통과유량과 수리구배(Lee, 2024), ln(h2)와 경과시간(Genereux et al., 2008), 그리고 ln(h1/h2)과 경과시간 간의 관계(Chen, 2000) 모두가 직선적인 상관관계를 갖는다(R² > 0.999, p-value < 0.05). Chen(2000)의 ln(h1/h2)과 경과시간 간의 관계가 선형적인 것은 시험당시 하천수위와 퍼미아미터 내 안정수위가 1 mm 안팎의 미세한 차이를 보여, 하천수위 기준의 가압수두나 안정수위 기준의 가압수두가 거의 같았기 때문이다.

Fig. 7.

Results of field falling-head permeameter tests. Each horizontal row represents test points, and each vertical column represents different methods. Lee: Flow rate vs hydraulic gradient. Genereux: ln(h2) vs elapsed time. Chen: ln(h1/h2) vs elapsed time.

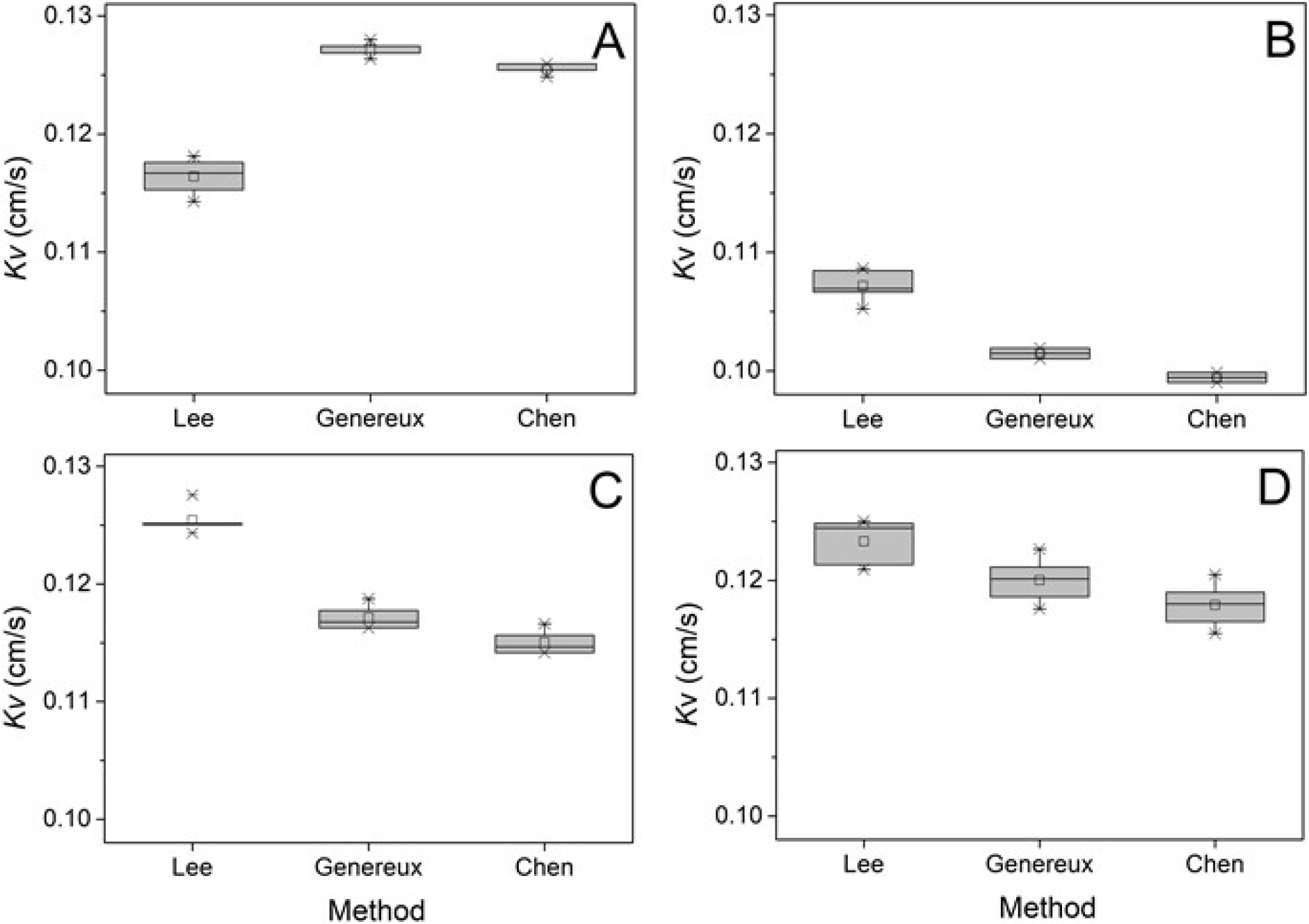
세 방법으로 산정된 4개 지점에서의 하상퇴적물의 Kv는 최소 0.099 cm/s, 최대 0.128 cm/s 에 이르며, 지점별, 방법별 큰 차이를 보이지 않는다(Fig. 8). A 지점을 제외하면 Lee(2024), Genereux et al.(2008) 그리고 Chen(2000) 방법의 순서로 Kv가 낮아지는 경향을 보인다. Lee(2024) 방법에 의해 결정된 A지점에서의 Kv 값들이 Chen(2000)과 Genereux et al.(2008) 방법에 의한 값들에 비해 작은 값을 갖는데, 이는 A지점에서의 퍼미아미터 삽입 심도(55 cm)가 다른 지점보다 깊어 퍼미아미터 내 퇴적물의 물성이 다른 지점과 다르거나, 퍼미아미터 내 퇴적물 하단부의 수위 측정 오차 때문인 것으로 추정된다. 4개 지점에서 Genereux et al.(2008)에 의한 Kv 값이 Chen(2000)의 값들 보다 일관되게 큰 이유는 식 (2)와 식 (3)의 차이 때문이다. 식 (3)의 m을 포함하는 항을 제외하면 식 (3)은 식 (2)와 동일하며, m을 포함하는 항이 식 (3)으로 결정되는 Kv 값을 증가시키기 때문이다. 특히 다른 두 방법에 비해 Lee(2024) 방법에 의해 산정된 Kv 값의 편차가 큰 특징을 보이는데, 이는 퍼미아미터 내 퇴적물 하단부의 수위 측정 오차에 의한 것으로 판단된다. 퍼미아미터 내 퇴적물 상부의 수위는 시험 동안 하천수위보다 높아 측정하기가 용이한 반면, Lee(2024) 방법에서 요구하는 퍼미아미터 하단부의 수위는 하천수위에 근접하여 정확한 수위 측정이 어렵다(Lee, 2024). 특히 시험 후반부로 갈수록 하천 수위와의 차이가 작아져 측정 정확도가 떨어지는 문제점이 확인된다. 최소 0.099 cm/s, 최대 0.128 cm/s에 이르는 세 방법에 의해 4개 지점에서 결정된 Kv 값들의 근소한 차이를 고려하면 퍼미아미터 하단부 수위 측정의 정확도가 Kv 값 결정에 큰 영향을 미치지 않은 것으로 판단된다.

Fig. 8.

Comparison of vertical hydraulic conductivity values derived from three analytical methods, based on field falling-head test data collected at four points (A~D) within the streambed sediments of Nosungcheon Stream.

결 론

하천, 강, 호수 등에서의 지하수와 지표수 간 상호작용을 심층적으로 이해하기 위해서는 지표수 퇴적물의 Kv를 정확하고 신속하며 간편하게 측정하고 분석할 수 있는 방법이 요구된다. 본 연구에서는 변수두 투수시험 결과를 분석하여 Kv를 산정하는 3가지 방법의 특성과 장, 단점을 비교하고 평가하기 위해 실내 및 현장 시험을 수행하였다. 연구 결과는 다음과 같이 요약된다.

(1) Chen(2000) 방법에 의한 Kv 값은 모래수조 내 물 흐름의 방향과 세기에 따라 크게 변동한다. 이는 Chen(2000) 방법에서 가압수두가 퍼미아미터 내 안정수위가 아닌 모래수조 수위를 기준으로 하였기 때문이다. 그러나 퍼미아미터 내 안정수위를 기준으로 가압수두를 적용하여 분석한 경우, 물 흐름의 방향과 세기에 관계없이 안정적인 Kv 값을 산출하였으며, 이는 Genereux et al.(2008) 및 Lee(2024) 방법의 결과와 근소한 차이를 보인다. 세 방법간 차이가 가장 큰 Δhrt = 46.0 cm 단계에서도 Chen(2000)과 Lee(2024) 간, Chen(2000)과 Genereux et al.(2008) 간 평균 Kv 값 차이는 0.004 cm/s와 0.001 cm/s 이다. 이럴 경우, 미지의 m에 대한 고려가 불필요하므로 Genereux et al.(2008) 방법보다 효율적인 것으로 판단된다. 그러나 퍼미아미터를 퇴적층에 삽입한 후, 안정수위 도달에 시간이 필요한 점은 여전히 현장작업에 불리하게 작용한다.

(2) Genereux et al.(2008) 방법에 의한 Kv 값은 물 흐름의 방향과 세기에 크게 영향을 받지 않으며, Lee(2024) 방법에 의한 값들과 큰 차이를 보이지 않는다. Kv 결정에 초기 수위를 이용하지 않아 Chen(2000) 방법에 비해 계산이 간편하다. 다만, Hvorslev equation(Hvorslev, 1951)에서 필요한 미지의 m 값에 대한 정보가 필요하며, 퍼미아미터를 퇴적층에 삽입한 후 안정수위에 도달하기까지 시간이 소요되는 문제가 있다(Lee, 2024). 특히, Chen(2000) 방법에 안정수위 기준의 가압수두를 적용하여 구한 Kv 값들이 Genereux et al.(2008) 결과와 근소한 차이를 보이는 결과는 Genereux et al.(2008) 방법에서 요구되는 미지의 m 값이 수직 수리전도도 결정에 크게 영향을 미치지 않음을 지시한다.

(3) Lee(2024) 방법은 퍼미아미터 내 퇴적물 상단부와 하단부의 수위를 활용해 통과 유량과 수리구배를 계산하여 Kv를 산출한다. 따라서 시험 전 안정수위 측정이나 미지의 변수 m에 대한 정보가 필요하지 않다는 장점이 두드러진다. Genereux et al.(2008) 방법에 따른 Kv 값과 비교해 큰 차이가 없으며, 물 흐름의 방향과 세기에 크게 영향을 받지 않는다(Lee, 2024). 그러나 현장 시험 시 퍼미아미터 하단부의 수위 측정 오차 문제를 고려하면, Chen(2000)과 Genereux et al.(2008) 방법과 상호 보완적으로 적용되어야 할 것으로 판단한다.