서 론
AI 개발
원형증강법
인공신경망
의사결정나무
오토 머신러닝
AI 예측 결과
매개변수
신뢰성 분석
예측N치 결과분석(E 프로젝트)
예측N치 결과분석(IA 프로젝트)
예측N치 결과분석(IN 프로젝트)
예측N치 결과분석(IP 프로젝트)
예측N치 결과분석(R 프로젝트)
예측N치 결과분석(M 프로젝트)
모델별 예측 결과분석
토질별 예측 결과분석
예측N치 3차원 분포
결론 및 고찰
서 론
플랜트, 토목 및 건축 사업에서는 대부분 지반 내 말뚝이나 얕은기초를 필수적 기초로 시공하고 있다. 구조물의 기초설계 시 기본 자료는 현장에서 실시한 시추조사와 표준관입시험의 N치를 가지고 적용하고 있다. 최근 플랜트 사업의 입찰기간은 짧은 시간 내에 공사견적비와 공사물량을 산정 하여 제출하는 조건이며, 초도진출국의 해외 입찰사업에서 부족한 시추조사와 표준관입시험 자료를 가지고 입찰과 공사에 참여할 경우 다수의 설계변경과 공기 증가 그리고 공사비 증가 등의 문제가 우려되고 있다(Kim et al., 2020). 이와 같은 부족한 지반자료의 불리한 여건을 해소하기 위해서 다수의 지반조사 자료만이 주요한 리스크 헷지 방법이나 입찰 시 현지 여건상 시추조사 인허가 승인문제, 시추 작업기간, 입찰 시 지반조사 과다비용, 민원 우려, 장비 진입불가 등 다수의 불리한 조건으로 시추조사가 어려운 것이 현실이다(Kim et al., 2020).
이와 같이 미비한 시추조사 자료와 표준관입시험 위치는 엔지니어들 마다 각자의 경험과 추정식 그리고 통계기법을 적용하여 N치를 추정하여 입찰 시 적용하고 있다. 하지만 경험과 추정식 그리고 통계기법 등으로 적용된 추정된 지반정보는 불확실성을 해소하기 어려우며 근본적인 문제를 해결하기 어려우며, 이는 말뚝의 설계 및 물량산정 오차로 이어져서 공기 지연 및 원가 증가의 원인이 되고 있다.
금회 연구는 시추자료와 표준관입시험이 없는 위치에서 실제와 가장 근접하게 신뢰성 있는 N치를 예측하는 기법을 개발하였으며, 최근 지질공학 분야에 적용되고 있는 AI 기술인 인공신경망과 의사결정나무 그리고 오토 머신러닝모델을 각각 적용한 후 회귀분석을 실시하였다(Kim et al., 2021). 각 모델을 적용하기 위하여 점토, 실트, 모래, 자갈 등으로 구성된 토질조건을 세립토인 점토와 조립토인 모래로 단순화 시켰으며, 모델별 매개변수를 다양하게 입력하는 시행착오 후에 신뢰도가 높은 N치를 예측하는 기법을 개발 할 수 있었다(Kim et al., 2021). AI에 의한 예측 결과의 신뢰성은 양호한 학습 자료의 존재여부가 핵심 변수이다. 본 연구에서는 학습 성능을 극대화하기 위해서 ‘원형증강법’을 적용하여 빅 데이터화 작업을 선행하였으며, AI 학습과정과 예측은 ‘Python 프로그래밍 언어’를 이용하여 코딩 하였다.
AI 개발
원형증강법
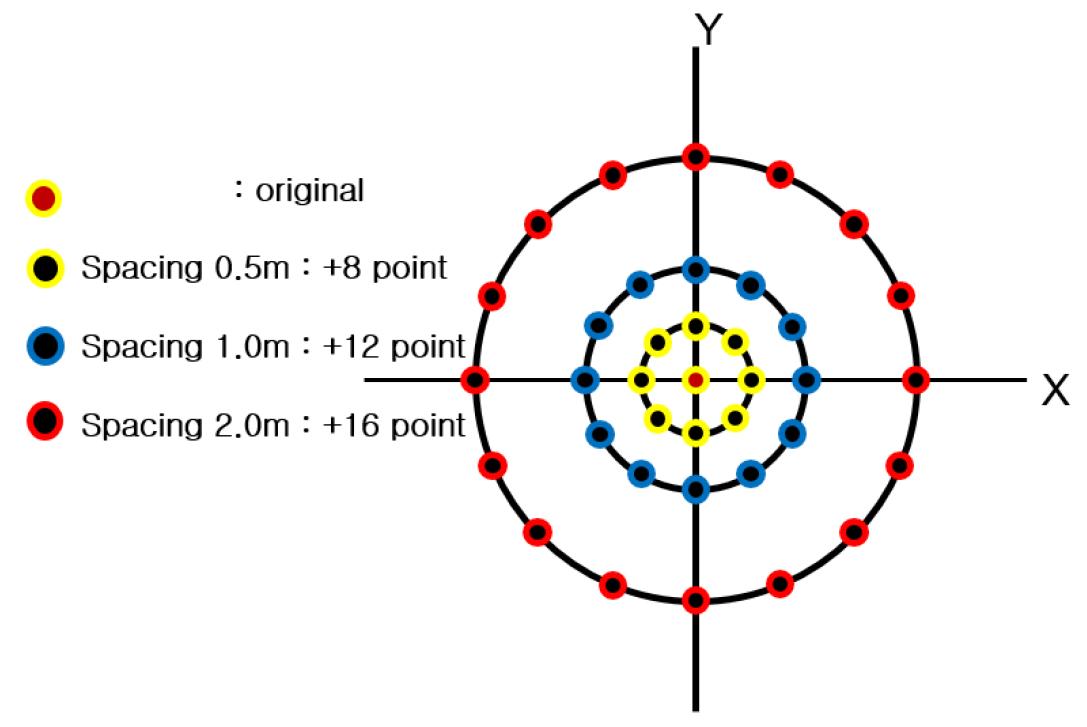
AI 학습 성능을 높이기 위해서는 양질의 학습 자료와 빅 데이터 존재가 중요하다. 본 연구에서는 부족한 시추자료를 빅 데이터화 하는데 다수의 노력이 필요하였으며 이를 위해 학습 자료에 ‘원형증강법’을 적용하여 시추반경 2 m까지 가상 N치를 생성 시켰다(Kim et al., 2021).
원형증강법이란 실측 지점을 기준으로 미리 정해진 시추 반경을 설정하여 방사형의 다수의 가상 포인트들을 설정하는 것으로, 실측 지점의 실제 시추공을 기준으로 반경 0.5 m에는 8개의 가상 포인트, 반경 1 m에는 12개의 가상 포인트, 반경 2 m에는 16개의 가상 포인트를 설정할 수 있다. 즉, 시추공 내 1건의 실측N치는 36건의 가상 N치가 추가되어 총 37건의 N치가 만들어 진다(Fig. 1). 예를 들어, E 프로젝트과 같이 시추공 20공에서 각 공별 실측N치가 16개인 경우, 320개의 실측N치를 획득하고, 아래 식 (1), (2)와 같이 총 11,840개의 빅데이터 N치를 확보할 수 있다.
원형증강법에 적용된 N치는 반경 2 m 이내로 N치의 변화가 없을 것을 가정한 것으로 심도별 실측 N값을 동일하게 적용한다. AI 학습을 위한 학습 자료와 예측을 위한 검증 자료 그리고 원형증강법에 의한 자료는 Table 1과 같다. 검증에 적용한 시추공은 AI 학습 성능을 파악하기 위한 것으로 학습에 적용되지 않은 시추공이며, 별도의 선정 기준 없이 각 프로젝트별 시추공에서 랜덤으로 선택하였다.
Table 1.
Training and testing data in AI method
본 연구에 적용된 자료는 학습 시추공은 106공, N치 2,219개 적용되었으며, 원형증강법에 의해 가상의 N치는 79,884개 생성되었다. AI는 이를 학습 후 N치를 예측하며 예측의 오차정도를 파악하기 위해 검증 시추공 55공, N치 1,200개로 분석하였다. 각 프로젝트별 학습과 검증 시추공이 다른 이유는 AI 학습에 최소한의 값을 이용하여 학습 가능여부 파악 후 예측 가능성을 연구하는 것이 주요 목적이기 때문이며 추후 연구는 학습 시추공을 감소시키고 검증 시추공을 증가 시켜 예측의 오차를 지속적으로 연구 할 것이다.
시추공 내 N치 값 중, 샘플러가 30 cm 이내에서 N치 50 이상의 단단한 지지층은 관입심도에 무관하게 N치 50을 적용하였다. 또한 AI 학습 입력값인 위도, 경도, Elevation, 심도, 토질 종류(점토, 모래)와 예측값 N치는 학습 성능을 높이기 위해서 전 ‧ 후처리 과정으로 0.0~1.0으로 정규화 하였다. 이 중 토질종류는 점토의 경우 0.5, 모래 1.0로 정규화 하였으며, 그 외는 각각의 최대값과 최소값으로 정규화를 적용하였다.
여기서, : 정규화 된 변수값, : 실제 변수, : 변수의 최대값, : 변수의 최소값
인공신경망
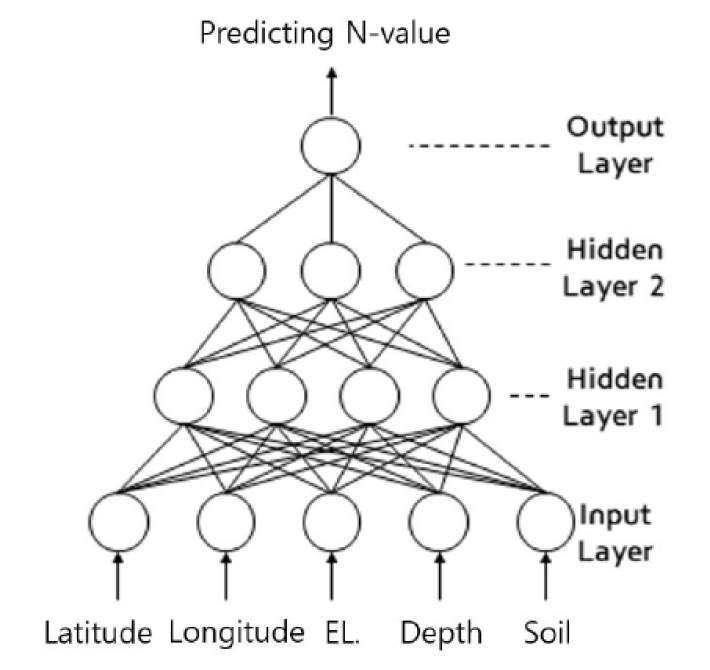
인공신경망은 입력층과 출력층 사이에 하나 이상의 은닉층이 존재하는 다층퍼셉트론으로 Fig. 2와 같은 계층구조를 갖으며, 오차역전파 학습 알고리즘을 이용하였다(Kim, 2002).이 기본 원리는 입력층 각각에 입력된 신호는 변환된 이후 은닉층에 전달되고 최종적으로 출력층에서 신호가 출력된다(Kim, 1989). 이와 같은 전달과정 중 최종 출력값과 초기 결정된 기대치는 상호 오차가 발생되며 이를 비교하면서 오차를 감소시켜 나가는 방법으로 연결강도()를 증감시켜 가고, 다시 출력층 부터 입력층의 역전방향으로 은닉층과 입력층은 다시 연결강도를 증감시켜 가는 학습이다(Kim, 1989). 즉 p번째의 입력, 목표출력 패턴이 제시되는 경우에 노드 i에서 노드 j로의 연결강도의 변화는 식 (4)와 같다.
인공신경망은 학습을 반복하는 동안 경사하강법으로 오차를 수정해 가며 ADAM(Adaptive moment estimation)을 적용하였다(Kingma and Ba, 2015). ADAM의 적용 식은 아래 식 (5), (6), (7)과 같으며 와 의 초기값을 0 벡터로 주면, 학습 초기에 가중치들이 0으로 편향되는 경향이 있다. 특히 붕괴율이 작으면, 즉 과 가 1에 근접할수록 편향이 더 심해지고 이 편향을 감소시키기 위해 아래와 같이 편향 오차()를 계산한다(Kingma and Ba, 2015).
최종적으로 업데이트 식은 다음과 같다.
금회 연구에서 추천값인 , , 그리고 learning rate()는 을 적용하였다. 인공신경망은 입력층과 2개 은닉층 그리고 출력층으로 이루어진 전방향 네크워크로 구성되어 있다(Kim et al., 2020). 입력층은 N치 예측을 위한 기본 자료를 입력하는 층으로 여기에 입력된 자료는 중간층을 거친 뒤 출력층을 통해 예측N치로 나오게 된다. 이 과정은 Fig. 2와 같이 나타내었다(Kim et al., 2020).
N치 예측을 위한 입력 자료로는 지반특성에 영향을 준다고 생각되는 인자들로 위도, 경도, Elevation, 심도, 토질 종류(모래, 점토)를 적용하였다(Kim et al., 2020). 본 연구에서 인공신경망은 ‘Keras’라이브러리를 이용하였으며, 조립토 조건인 자갈은 모래지반으로 세립토 조건인 실트는 점토지반으로 분류하여 AI를 학습시켰다. 이는 상세한 토질분류의 관점보다는 조립토와 세립토의 조건으로 단순화 하여 학습하기 위함이다.
의사결정나무
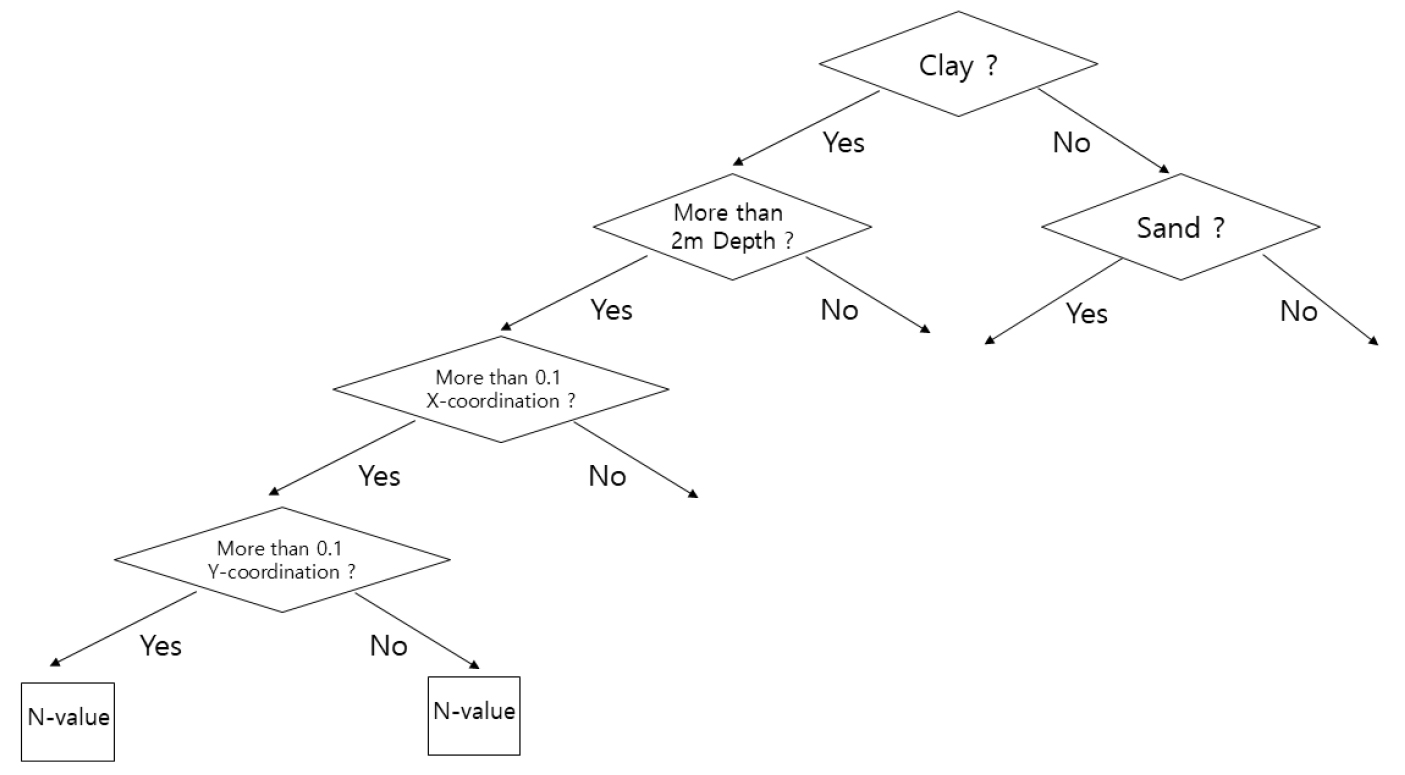
의사결정나무는 회귀분석과 분류분석 모두 가능한 지도 학습 모형 중 하나이다. 이러한 의사결정나무는 ‘예’ 또는 ‘아니오’ 질문을 이어나가는 스무고개 놀이와 비슷한 형식의 머신러닝 알고리즘이라고 할 수 있다(Navada et al., 2011). 트리의 구조는 크게 모든 자료집단을 포함하는 최상위 노드인 뿌리 노드, 더 분리되지 않는 최하위 노드인 잎 노드, 잎 노드는 아니지만, 자식 노드를 가지고 있는 중간 노드인 내부 노드로 구성된다. 그리고 상위 마디를 부모 노드라 하고, 하위 마디를 자식 노드라고도 칭한다(Jeong et al., 2021). 의사결정나무의 구성에 대한 예시는 Fig. 3과 같으며 ‘LightGBM(Gradient boosting machine)과 XGBoost(Extreme gradient boosting)’라이브러리를 적용하였다(Chen and Guestrin, 2016).
오토 머신러닝
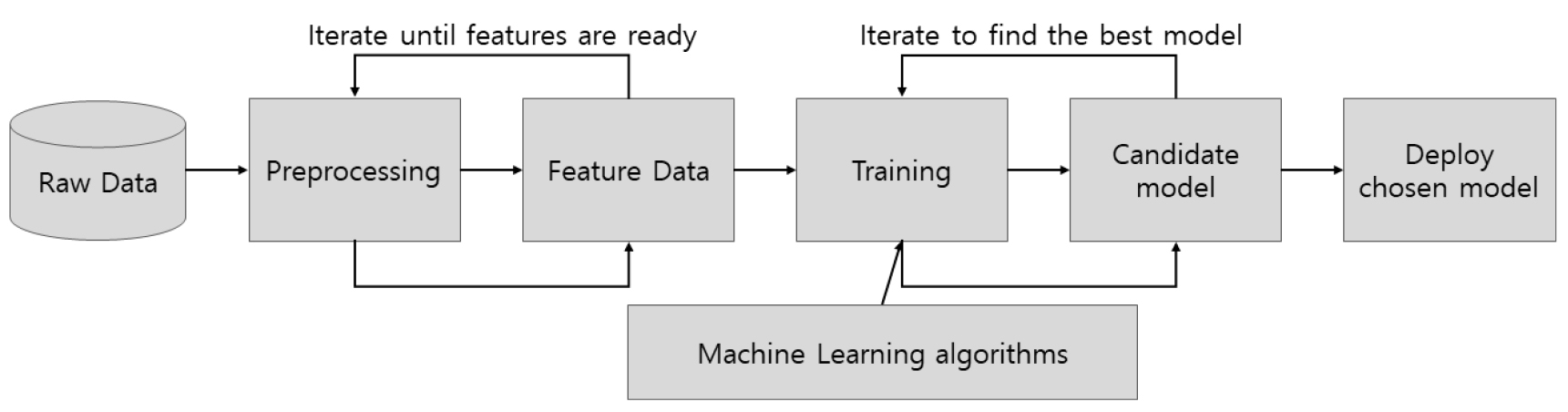
머신러닝 모델을 개발하고 실제 운영에 도입하기에는 수많은 과정을 거치게 된다(Fig. 4). AI가 존재하여 컴퓨터와 데이터만 주어지면 모든 과정을 알아서 해결해 줄 수 있다면 좋겠지만, 현실의 머신러닝 모델링은 문제 정의 과정에서부터 데이터 수집, 전처리, 모델 학습 및 평가를 거쳐 서비스 적용에 이르기까지 여러 분야 전문가들의 많은 시간과 노력이 요구된다(Ferreira et al., 2021).
오토 머신러닝은 머신러닝을 적용할 때 마다 이러한 과정을 되풀이하면서 발생하는 비효율적인 작업을 최대한 자동화하여 생산성과 효율을 높이기 위하여 등장하였다(Zöller and Huber, 2021). 특히, 데이터 전처리 과정에서부터 알고리즘 선택 및 튜닝까지의 과정에서 모델 개발자의 개입을 최소화 하여 품질 좋은 모델을 효과적으로 개발할 수 있는 기술에 대한 연구가 오랫동안 진행되어 왔다(Zöller and Huber, 2021).
최근 머신러닝 분야의 발전과 관심에 힘입어 오토 머신러닝 기술을 머신러닝 모델 개발 시에 손쉽게 적용할 수 있는 package toolkit들이 연구 개발되어 오고 있다(Olson et al., 2016). 금회 연구에서는 이 중 ‘TPOT(Tree-based pipeline optimization tool)’라이브러리를 적용하였다.
AI 예측 결과
매개변수
이번 연구에 적용된 AI 모델은 인공신경망, 의사결정 나무와 오토 머신러닝 세 가지 이며, 각 라이브러리의 활용을 위해서는 각각 매개변수가 고려된다. 이 중 대표적인 매개변수는 Table 2와 같이 적용 후, ‘Python ver. 3.8.12’프로그래밍언어를 이용하여 프로젝트별, 모델별로 각각 실행하였다.
이들 중 LigthGBM 라이브러리의 매개변수인 ‘num leaves’는 트리 모델의 복잡성을 제어하는 변수이며, ‘max 심도’는 트리 모델의 깊이를 제어하고 ‘objective’는 특정 문제에서 최대화되거나 최소화 되어야 하는 목적값을 나타낸다. 또한 TPOT 라이브러의 매개변수로 적용되는 ‘generations’은 파이프라인의 최적화 프로세스 실행에 대한 반복횟수이며, ‘population size’는 각 generation 마다 유전 프로그래밍 인구에 보유할 고유 모델의 가짓수이고 ‘scoring’은 문제에 대해 주어진 파이프라인의 품질을 평가하는 함수이다.
Table 2.
Applied parameters
신뢰성 분석
AI의 학습은 프로젝트별, 위치별 그리고 심도별 각각 수행 후 N치를 예측하였으며, 신뢰성을 높이기 위해 각 모델별 오차를 분석 후 최적의 AI 모델을 선정하였다. 적용된 신뢰성 분석은 평균절대편차(mean absolute deviation, MAD), 평균절대백분율오차(mean absolute percent error, MAPE)이며 식 (8), (9)와 같다(Kim, 2002).
여기서, : 실측N치, : 예측N치
이와 같은 식을 적용한 통계분석 결과는 각 지점별 실측자료와 예측N치를 가지고 분석하였다. AI는 세 가지 모델을 사용하여 각각 학습을 실시하였으며, 예측의 타당성을 분석하기 위해여 실측값과 예측값을 각각 비교하였다. 이 결과 각 프로젝트별 오차값은 Table 3과 같이 분석되었다.
Table 3.
Calculated mean absolute percent errors (MAPE)(unit: %)
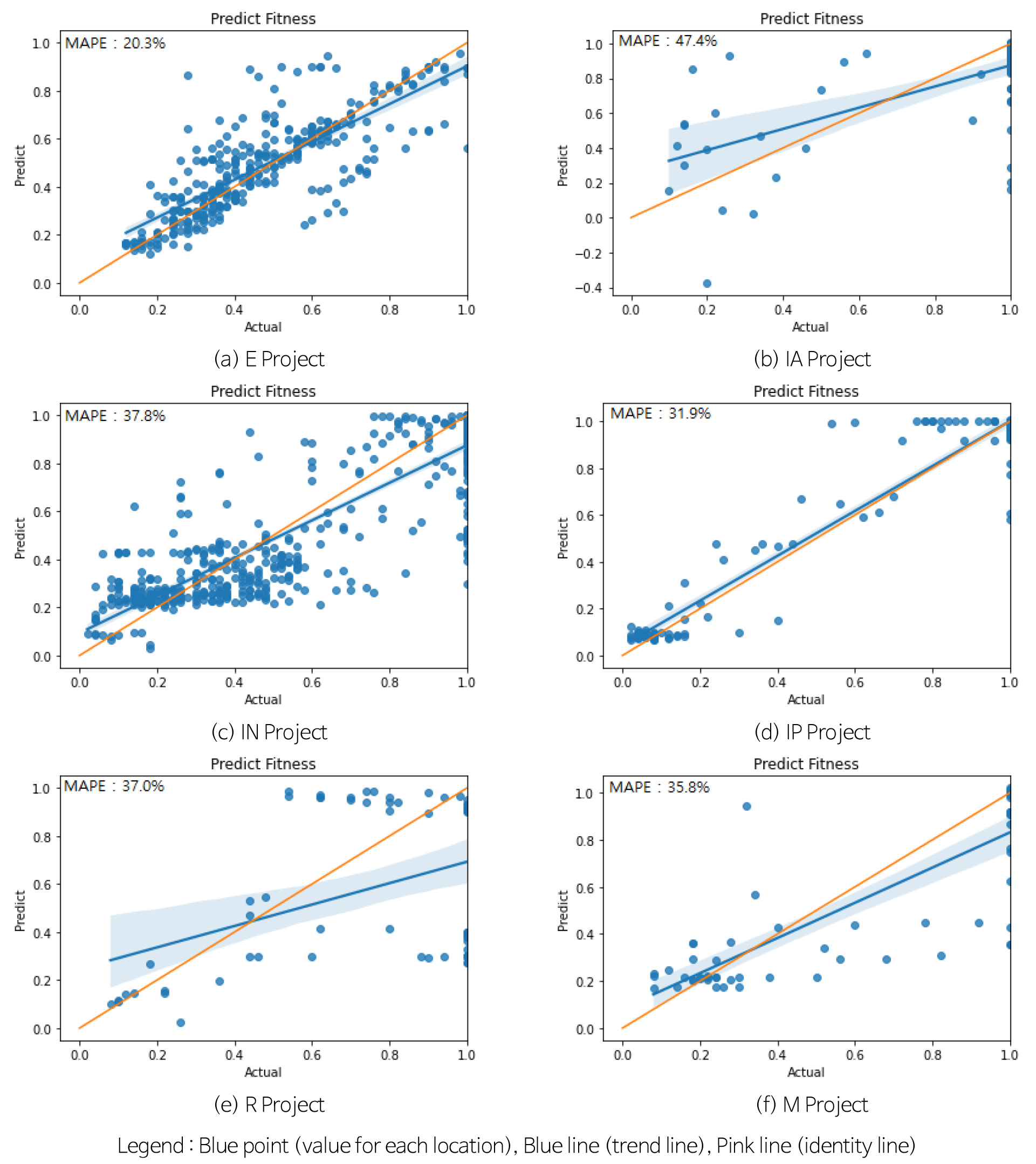
MAPE 분석결과, 오토 머신러닝은 20.3~59.3%, 의사결정 나무 23.7~88.2% 그리고 인공신경망은 53.0~139.2%로 과다한 경향이 나타났다. 이 자료에 근거 할 때 오토 머신러닝인 TPOT과 의사결정 나무의 LightGBM이 대체적으로 신뢰도가 높은 편이며, 특히 TPOT이 다소 양호한 신뢰도를 나타내고 있는 것으로 분석되었다. 이 때 비교된 실측값은 AI 학습에 적용하지 않은 시추공의 N치를 사용하였으며, 학습 성능을 높이기 위해 입력값과 결과값은 0.0~1.0으로 정규화 하였다. 각각의 AI 모델별 N치를 예측한 후 실측값과 비교 ‧ 검토하였으며 각 프로젝트별 적용한 결과는 Fig. 5와 같다. E 프로젝트, IN 및 IP 프로젝트는 실측값과 예측값의 유사한 분포를 나타내고 있어서 신뢰도가 높은 것으로 분석되었다. 그 외 IA, R, M 프로젝트는 실측값과 예측값의 신뢰도가 다소 부족하여 각각 시추공에서 상세히 검토 하였다.
인공신경망은 최적화에 많은 시행착오가 필요하고, 다른 모델 대비 오차값이 상대적으로 과다하여 최종 예측모델에서는 제외 시켰다. 금회 N치 예측에 적용된 MAPE는 상대적인 증감을 표현하기 때문에 N치 예측 성능 평가는 한계성이 있으며, 추후 연구 시 신뢰성 분석은 평균절대편차(MAD)가 보다 타당함을 알 수 있었다.
예측N치 결과분석(E 프로젝트)
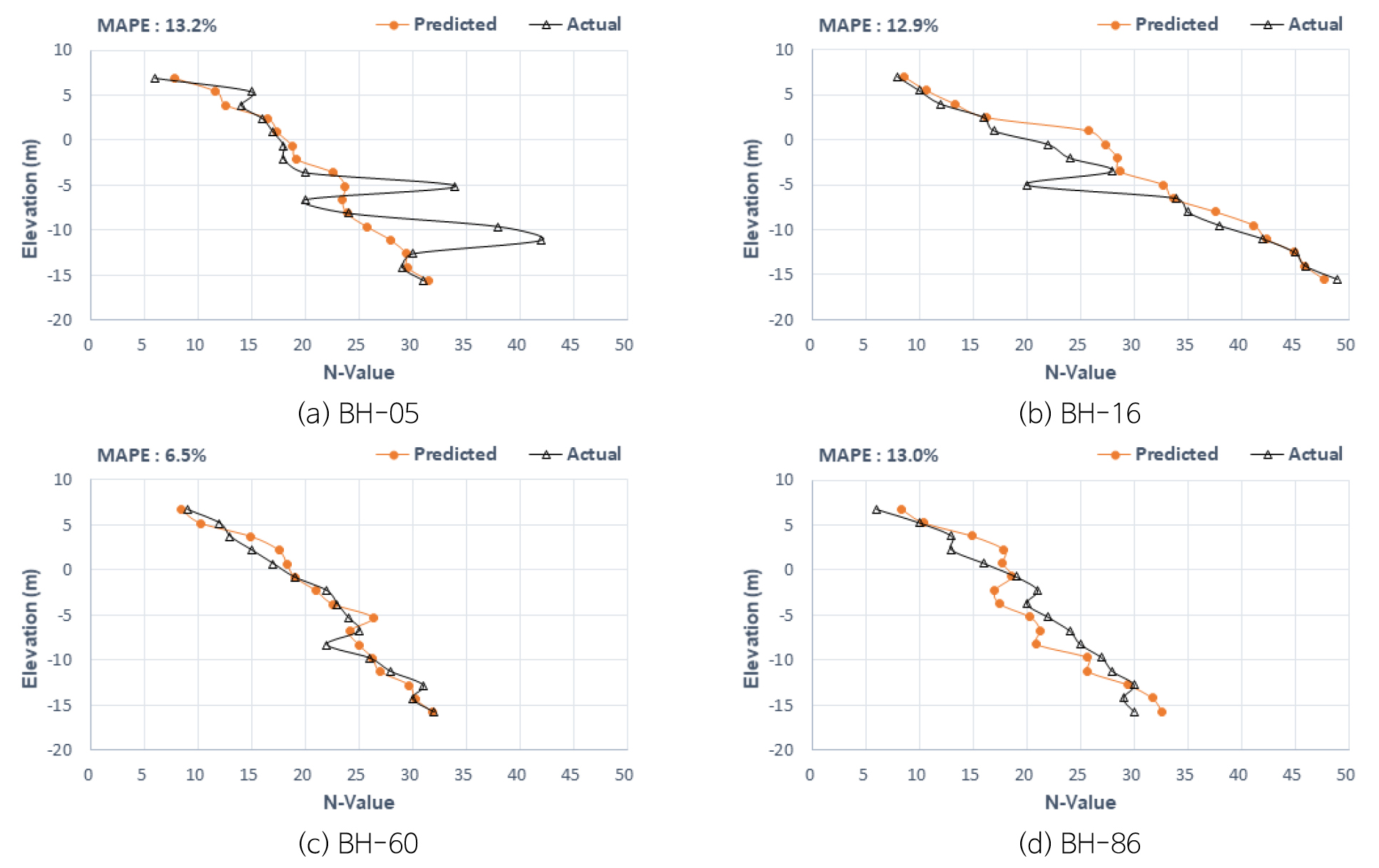
AI의 예측성능을 파악하기 위해 예측값과 실측값을 각 시추공별로 비교 ‧ 검토하였다. Test에 적용된 실측값 시추공은 학습에 이용되지 않았으며, 예측 성능을 확인하는데 중요한 검증 자료로 사용하였다. E 프로젝트에서 적용한 AI는 TPOT 라이브러리이며 예측값과 실측값의 대표적인 결과는 Fig. 6과 같다.
통계분석결과, MAPE는 6.5% 이상의 오차값이 분포하며 심도 하부로 갈수록 N치가 증가되는 경향을 보인다. 심도 EL.-15 m 이하에서 대부분 N치 30~40 정도로 실측값과 유사하게 예측되었다.
(BH-05)번공은 MAPE가 13.2%로 분석되며, EL.-5~-10 m 구간의 일부 실측값이 작게 예측되나 그 이외는 유사한 경향으로 예측되는 것으로 분석되었다. (BH-16)번공도 MAPE가 12.9%로 신뢰도 양호한 예측으로 분석되며, 실측값과 유사한 N치 분포로 예측되고 있다. EL.-10 m 이하에서 N치 40 이상의 지지층이 실측값과 유사하게 예측되고 있다. (BH-60)번공은 MAPE가 6.5%로 가장 신뢰도가 양호한 예측으로 분석되며, 실측값과 유사한 N치 분포로 예측되고 있다. 이 현장은 심도가 깊어질수록 N치가 증가하는 경향을 보이며 EL.-15 m 이하에서 N치 30 이상이 예측되고 있다. (BH-86)번공은 MAPE가 13.0%로 양호한 예측으로 분석되며, EL.0~-12 m까지는 예측값이 작게 예측이 되며 그 이외에서는 실측값과 유사한 경향으로 예측되고 있다.
예측N치 분석결과, EL.-15 m 이하에서 N치 30~35 정도 예측되고 있고 있으며 모래로 구성된 E 프로젝트의 추정 지반정수는 내부마찰각 33~39°정도 양호한 지반으로 예측 할 수 있다. 또한 지표에서 EL.-10 m까지는 N치가 2~25 정도이며, 추정 내부마찰각은 20~32°정도로 심도가 깊어질수록 양호한 지반조건으로 분포되어 있다.
E 프로젝트에 적용한 TPOT 라이브러리 학습결과는 실측값과 유사한 경향을 보이고 있으며, 예측결과를 통하여 말뚝의 지지력 산정에 적용될 수 있는 심도별 N치 분포를 쉽게 파악 할 수 있었다. 금회 연구는 세립토인 점토와 조립토인 모래로 두 가지 조건으로 실시하였으며, 실트와 자갈은 세립토와 조립토로 포함시켜 적용하였다. 또한 N치 10 이하의 연약지반에 대한 조건까지 심도 있는 연구진행이 요구된다.
예측N치 결과분석(IA 프로젝트)
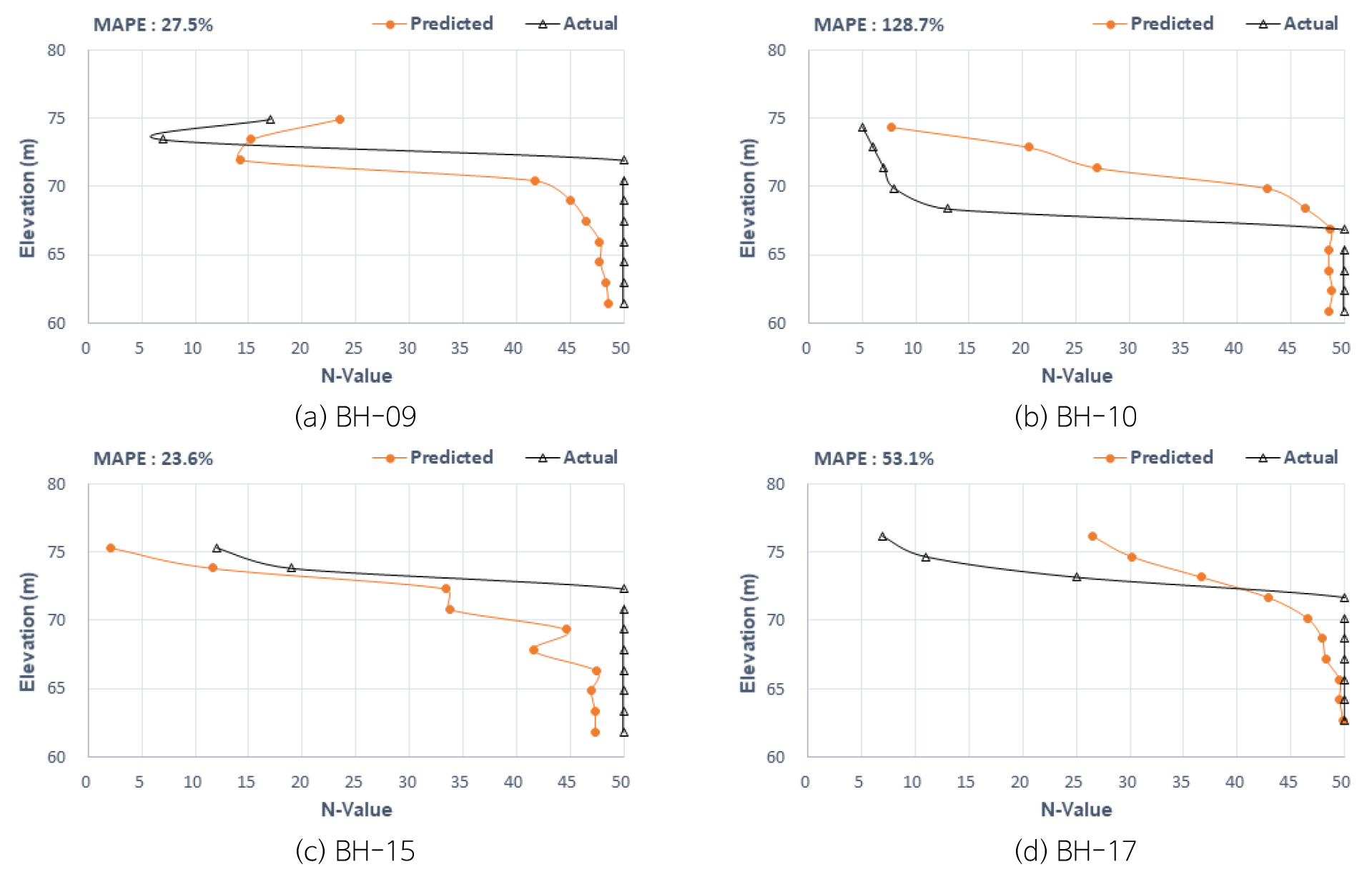
IA 프로젝트에서 적용한 AI는 LightGBM 라이브러리이며 예측값과 실측값의 대표적인 결과는 Fig. 7과 같다. 통계분석결과, 지표에서 심도 -5 m까지는 예측이 실측값과 일부 차이가 나는 경향으로 MAPE가 높으며 신뢰도가 낮게 나타나고 있다. 이는 지표에서 심도 -5 m까지 연약한 점토지반이나 그 하부는 단단한 지지층이 급격히 발생되는 지반조건으로 급변하는 지반 특성에는 예측에 오차가 발생되고 있다. 이와 같은 지표인근과 저부에서 지반특성이 급변하는 조건에서는 보정값 적용이 필요하다. 추가 연구 시 보정값을 적용 방안을 고려할 것이다. 보정 방안은 연약층과 단단한 지지층을 이중층으로 분리하여 각각 AI를 학습시키는 방안을 고려하고 있다.
공별 분포 결과, 심도 하부로 갈수록 N치가 증가되는 경향을 보인다. 지표에서 심도 -10 m까지 예측 N치는 45 이상의 단단한 지지층으로 실측N와 유사한 값으로 예측하고 있다.
(BH-09)번공은 MAPE가 27.5%로 분석되며, 대체로 실측값보다 작게 예측되는 경향을 보이고 있으나 EL.70 m 이하에서는 실측값과 유사한 경향의 지지층 분포를 파악할 수 있었다. (BH-10)번공은 지표에서 EL.65 m까지 예측값이 과다하게 예측되는 경향을 보여서 MAPE 128.7%로 신뢰도가 낮게 분석되었으나 하부심도에서 말뚝 지지층을 파악하는데 유사한 경향으로 예측되고 있다. (BH-15)번공은 MAPE가 23.6%로 분석되며, 실측값보다 작게 예측되는 경향을 보이고 있으나 EL.70 m 이하에서는 실측값과 유사한 경향의 지지층 분포를 파악할 수 있었다. (BH-17)번공은 MAPE가 53.1%로 신뢰도가 낮은 값이 나타나지만 EL.70 m 이하에서는 실측값과 유사한 말뚝 지지층을 파악할 수 있었다.
예측N치 분석결과, 지표에서 연약지반에서 N치 2~20 정도이며, 지지층이 분포하는 고심도에서 N치가 45 이상으로 실측치와 유사한 분포로 예측된다. 점토로 구성된 IA 프로젝트의 추정 지반정수는 지표에서 EL.65 m까지 점착력 12~270 kN/m2로 추정되며 지표인근은 연약지반으로 추정되고 있다. EL.65 m 이하는 점착력 280 kN/m2 정도, 변형계수 30,000~45,000 kN/m2 정도 양호한 지반조건이 추정된다.
IA 프로젝트는 지표에서 심도 -5 m까지는 점토성분의 토질분포를 나타내고 있으며 이하심도에서 지지층이 존재하는 경향이며, 지표인근의 저심도 부근에 N치를 신뢰도 높게 예측하는 추가적인 연구개발이 요구되고 있다. 지표인근과 저부에서 예측값은 실측값과 오차가 크게 발생되는 주요 원인은 지표 인근에서 학습 N치의 변화 폭이 과다하다 보니, AI 학습성능이 떨어지고 있으며, 추가 연구 시 연약층과 단단한 지지층을 이중층으로 분리하여 각각 AI를 학습시키는 최적의 모델 알고리즘 선정과 시행착오를 통한 매개변수 선정 방안이 요구되고 있다.
예측N치 결과분석(IN 프로젝트)
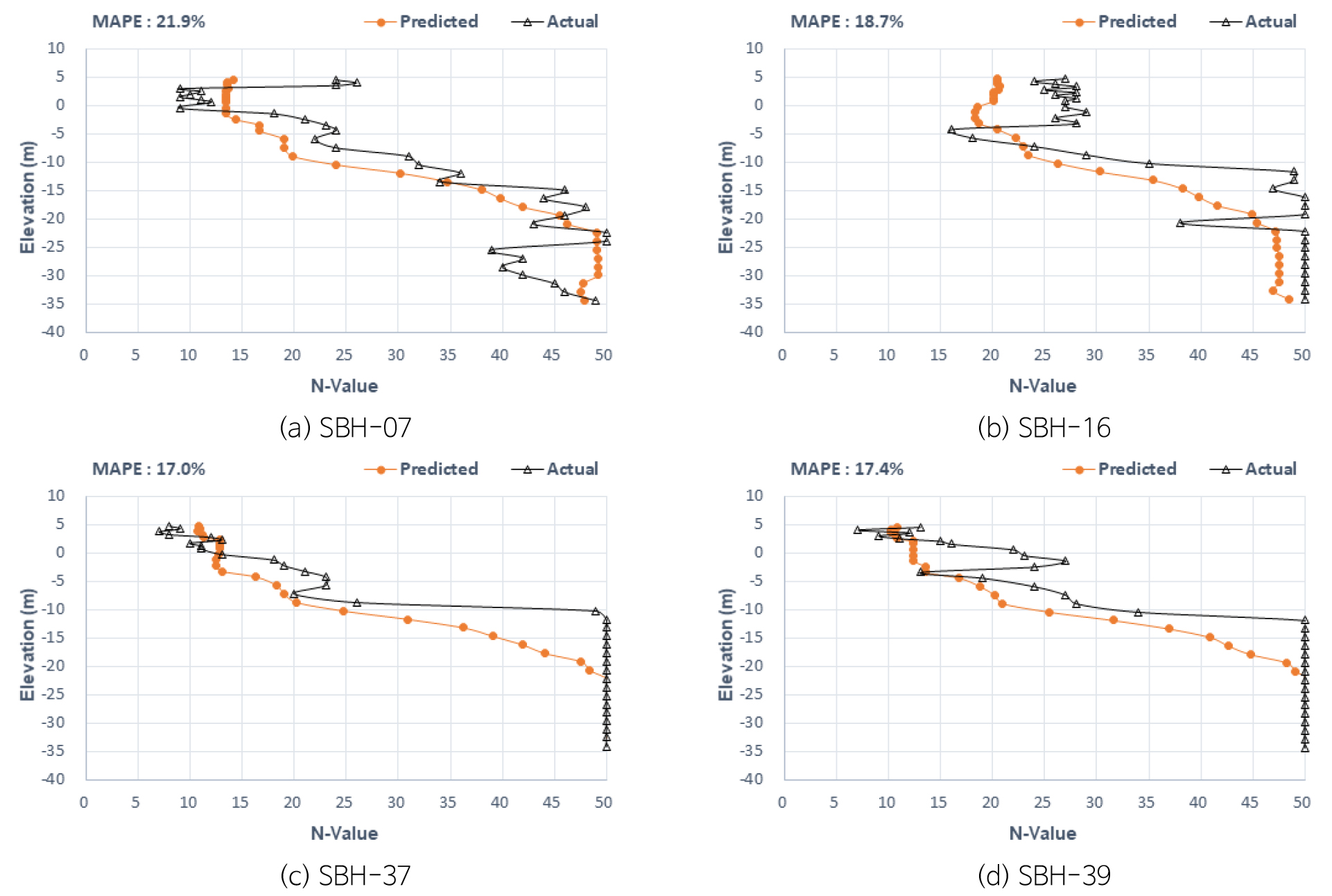
IN 프로젝트는 TPOT 라이브러리를 적용하였고 예측값과 실측값의 대표적인 결과는 Fig. 8과 같다. 통계분석결과, 지표에서 EL.-15 m까지는 예측이 실측값과 일부 차이가 나는 경향으로 MAPE 신뢰도가 낮게 나타나고 있다. 이는 상하 지반에서 불규칙한 분포를 보이는 지반조건에서는 예측의 한계를 나타내고 있다. 이러한 지반에서 보정값을 적용하는 방안을 추가로 연구할 필요가 있다.
(SBH-07)번공은 MAPE가 21.9%로 분석되며, 지표에서 EL.-15 m까지는 대체적으로 실측값보다 작게 예측되는 경향을 보이고 있으나 EL.-15 m 이하에서는 실측값과 유사한 N치 40 이상의 지지층을 예측하고 있다. (SBH-16)번공은 MAPE 18.7%로 양호한 편이나 대체적으로 실측값보다 작게 예측되고 있으며 지지층 심도의 경향을 파악할 수 있다. 그 외 (37, 39)번공에서 실측값보다 작은 N치가 예측되는 경향을 보이나 심도별 지층의 분포와 지지층의 특성은 유사한 예측을 보이고 있다. 이 시추공은 EL.-10~-20 m 구간은 실측값이 이암층으로 N치 50정도이나 예측값이 작게 나타나고 있어 오차가 발생되고 있는 경향이 있다.
예측N치 분석결과, 지표에서 EL.-10 m까지는 N치 10~25 정도 예측되며 EL.-20 m 이하는 N치 45 이상이 예측된다. 지표에서 EL.-10 m까지 점토로 구성된 추정 지반정수는 점착력이 60~155 kN/m2로 추정되며, EL.-10 m 이하에서는 점착력 280 kN/m2 이상, 변형계수 30,000~45,000 kN/m2 양호한 값이 추정된다.
IN 프로젝트는 심도 하부로 갈수록 N치가 증가되는 경향을 보이며, EL.-20 m 이하에서 대부분 예측N치 40 이상으로 단단한 실제 지지층과 흡사하게 예측되고 있다.
이는 대체로 지지층의 분포가 비슷한 편이나 예측값은 상대적으로 약 10 m 이상 더 깊은 곳에서 N치 50이 예측되는 경향을 보이고 있다. 이는 지반 내 존재하는 불확실성이 일부 N치가 증가되는 구간에서 예측을 어렵게 만들기 때문이다. 하지만 말뚝 지지층 파악을 위한 N치 40~50 정도는 실측값과 유사하게 예측되고 있어서 지지층 파악을 하는데 유용하게 이용 될 수 있다.
예측N치 결과분석(IP 프로젝트)
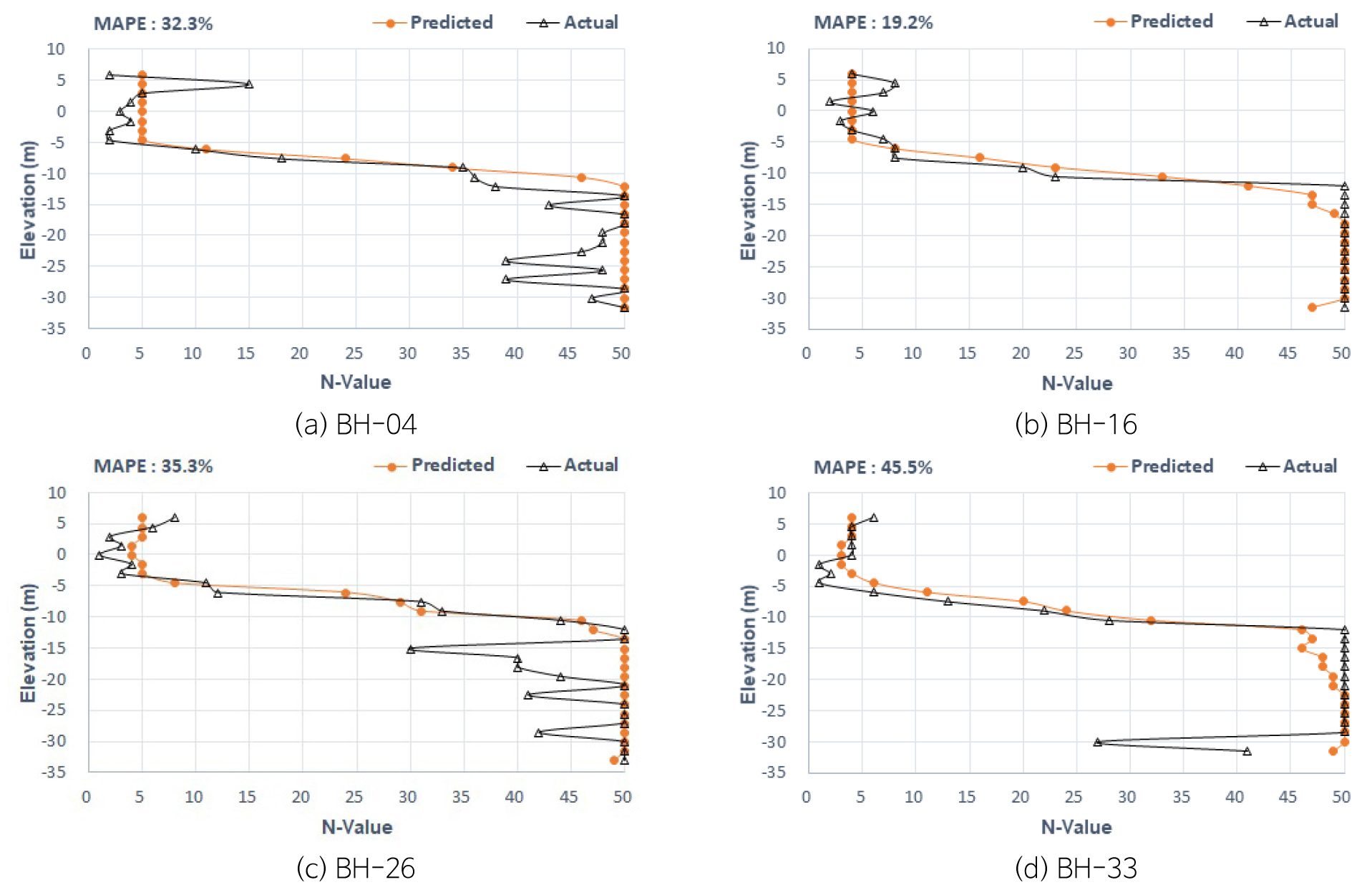
IP 프로젝트는 TPOT 라이브러리를 적용하였고 예측값과 실측값의 대표적인 결과는 Fig. 9와 같다. 통계분석결과, EL.5~-5 m까지는 예측값이 N치 5로 예측되며, EL.-12 m 이하에서는 N치 45 이상의 값을 예측하고 있다. 예측값의 MAPE는 19.2~45.5%까지 오류값이 나타나지만 심도별 지반특성의 경향은 유사하게 예측되고 있다. (BH-4, 26)번공은 EL.-12~-35 m 구간에서 실측값이 불확실성의 존재로 N치가 불규칙적이며 예측값은 N치 50으로 예측되고 있어서 이에 대한 오차가 발생하는 것을 확인 할 수 있었다.
예측N치 분석결과, 지표에서 EL.-5 m까지는 N치 5 정도 예측되며 EL.-10 m 이하는 N치 47~50이 예측된다. 점토로 구성된 추정 지반정수는 지표에서 EL.-10 m까지 점착력 30 kN/m2로 연약한 지반이 예측되며, EL.-10 m 이하에서는 점착력 290~310 kN/m2 정도, 변형계수 30,500~50,000 kN/m2 그리고 수평지반반력계수는 33,000~33,800 kN/㎥ 양호한 값이 추정된다.
IP 프로젝트는 지반분포가 점토와 이암으로 구성되어 있으며, 이암의 풍화정도에 따라 나타나는 N치 30~50 구간에서 불확실성에 대한 오류로 한계성을 나타내고 있으며 이에 대한 추가적인 연구가 요구된다. 또한 건기, 우기철 지하수위 변동 조건에 대하여 추가로 고려가 필요하며, 특히 이암 구간에서 지하수위 조건별 풍화정도가 다르게 나타나고 있어서 이에 대한 연구가 요구되고 있다.
예측N치 결과분석(R 프로젝트)
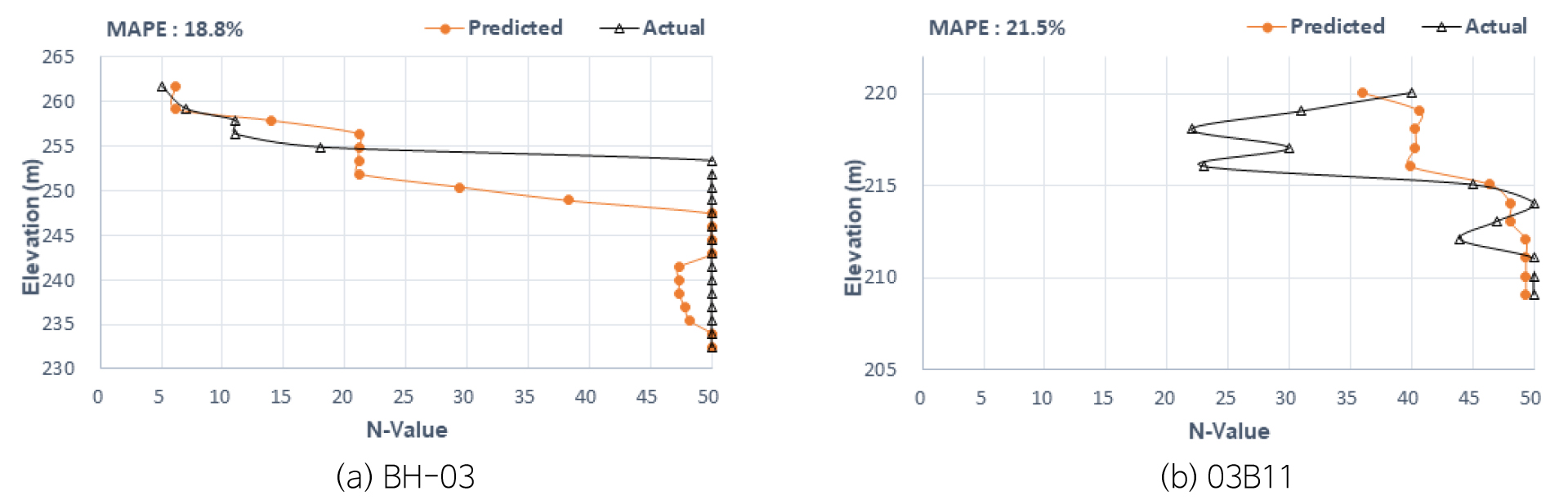
R 프로젝트는 TPOT 라이브러리를 적용하였고 예측값과 실측값의 대표적인 결과는 Fig. 10과 같다. 분석결과, 실측값은 이암과 점토로 구성된 조건의 지반으로 (BH-03)번공은 MAPE가 18.8%로 양호한 편이며, 예측값은 N치 50인 분포는 심도가 EL.247 m 이하에서 나타나며 실측값 보다 7 m 더 깊은 곳에서 예측되고 있다. 이 예측값을 이용하여 말뚝 설계 시 오류를 발생시킬 수 있으므로 이러한 곳은 추가적인 시추조사가 필요하며, 학습 자료를 증가시켜야 할 것으로 파악되었다.
(03B11)번공은 지표에서 EL.215 m까지는 실측값보다 크게 예측되고 있으며 그 이하는 실측값과 유사하게 예측되고 있다. 이 시추공의 예측은 EL.220~215 m 구간에서 실측값보다 N치가 15정도 더 크게 예측되고 있어서 이에 대한 보정이 요구된다. 말뚝 설계 시 주면지지력 산정 시 N치 15 차이는 설계 오류를 야기 시킬 수 있으므로 추가적인 시추조사를 통해 학습 자료 습득이 필요한 여건이다. 또한 R 프로젝트는 충적층으로 분포된 지층이며 상부는 지하수위 변동이 크게 일어나고 있어서 이에 대한 추가로 연구가 필요하다.
R 프로젝트는 학습 7개 시추공의 작은 편으로 빅데이터 생성을 하여도 학습 오류에 대한 문제가 야기되고 있으며 다수의 시행착오가 필요했다. 학습 자료가 부족한 여건에서 예측하는 기법에 대한 심도 있는 연구가 추가 요구되고 있으며, 부족한 자료를 이용하는 머신러닝 라이브러리 함수의 연구개발이 요구되고 있다.
예측N치 결과분석(M 프로젝트)
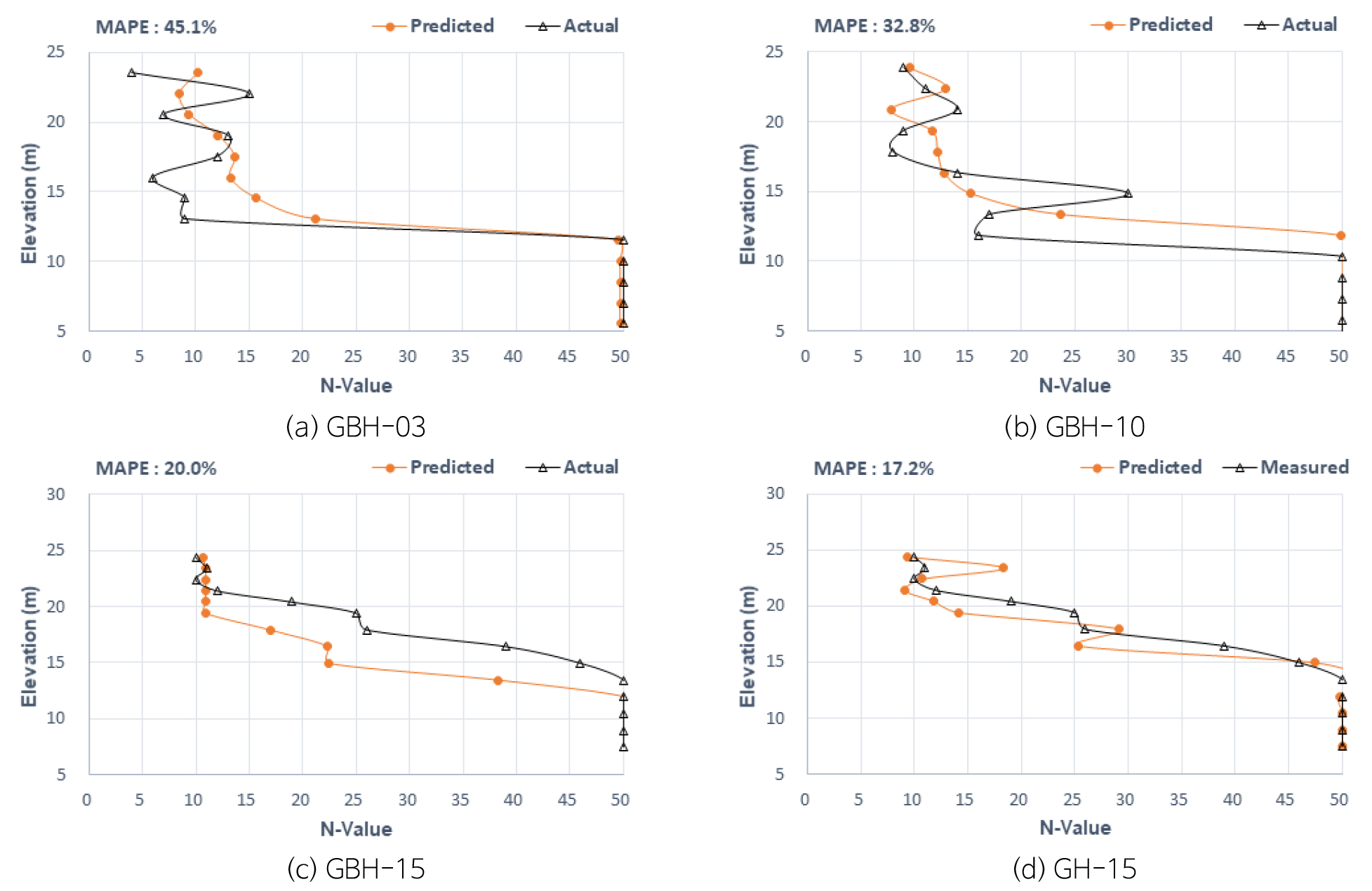
M 프로젝트는 LightGBM 라이브러리를 적용하였고 예측값과 실측값의 대표적인 결과는 Fig. 11과 같다. 통계분석결과, 예측값의 MAPE는 17.2~45.1%로 오류값이 나타나지만 심도별 지반특성의 경향은 유사하게 예측되고 있다.
(GBH-03)번공은 지표에서 EL.12 m까지는 예측값이 크게 나타나고 있으며 그 이하 심도에서는 실측값과 유사한 N치 50이 예측되고 있다. (GBH-10)번공은 지표에서 EL.17~12 m까지 예측값이 실측값보다 크게 예측되고 있으며, 그 이하 심도에서는 실측값과 유사한 N치 50이 예측되고 있다. (GB-15)번공은 대부분 심도에서 실측값과 유사한 경향으로 예측되고 있다. 이 시추공은 예측값이 실측값보다 약간 작게 나타나며, EL.12 m 이하는 N치 50이 유사하게 예측되고 있다.
예측N치 분석결과, 지표에서 EL.15 m까지는 N치 10~25 정도 예측되며 EL.10 m 이하는 N치 50이 예측된다. 점토로 구성된 추정 지반정수는 지표에서 EL.15 m까지 점착력 60~150 kN/m2로 연약한 지반이 예측되며, EL.15 m 이하에서는 점착력 310 kN/m2 정도, 변형계수 50,000 kN/m2 정도 양호한 값이 추정된다.
미시추 구간은 이를 이용하여 말뚝 기초의 지지력 산정이 가능할 것으로 분석되었다. M 프로젝트는 MAPE는 최대 32.8%까지 분석되나 미시추 구간에서 지지층 심도를 예측하고 싶을 경우 이와 같은 방법을 적용한다면 신뢰성 높은 설계가 가능할 것으로 분석되었다.
모델별 예측 결과분석
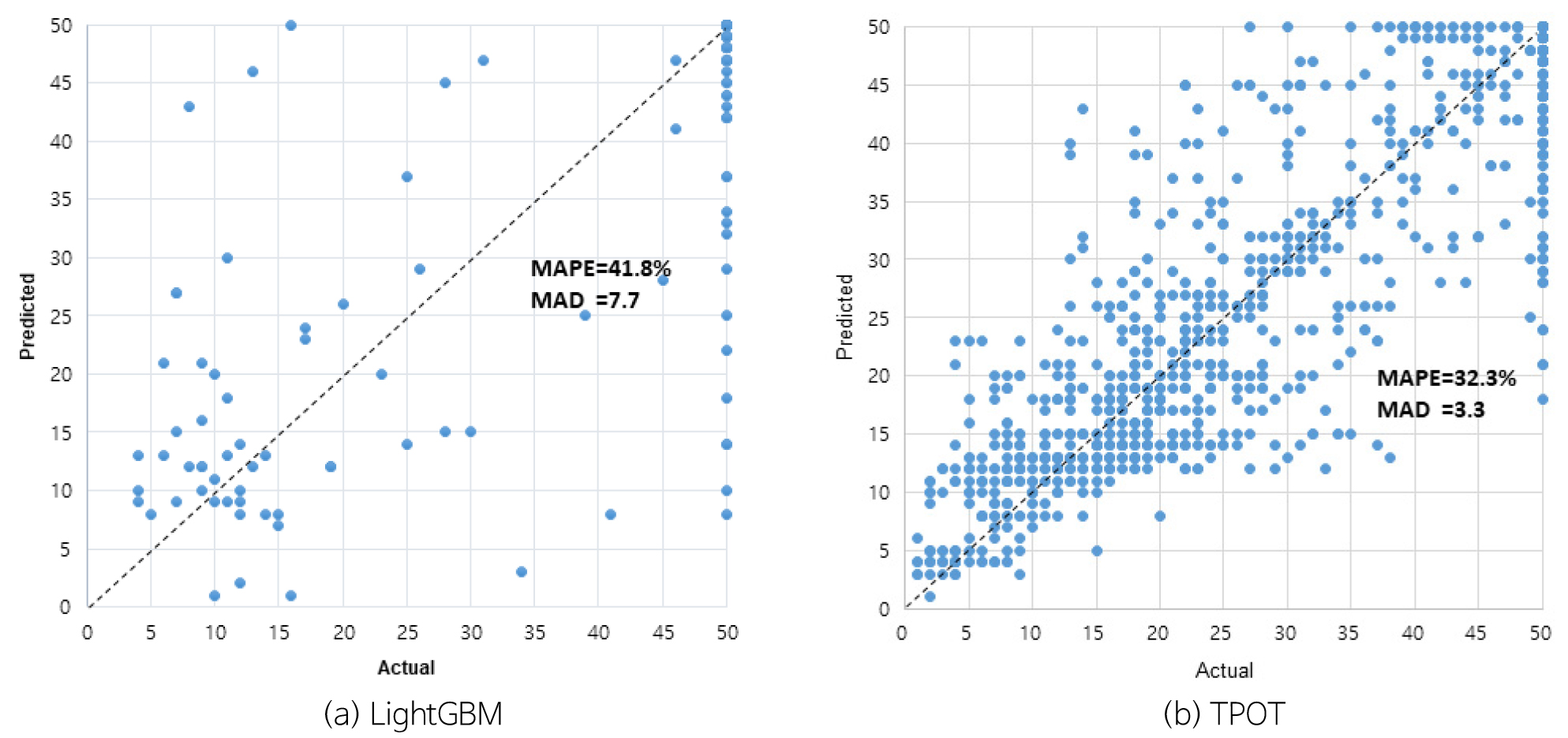
AI 예측은 6개 프로젝트에서 모델별 수행 후, 최소 오류값을 가지고 적용하였다. 주요 모델 중 LightGBM은 2개 프로젝트(IA, M)와 TPOT은 4개 프로젝트(E, IN, IP, R)에 적용하였으며, 각각 예측값과 실측값의 결과는 Fig. 12와 같다.
LightGBM를 적용한 예측값은 MAPE 41.8%, MAD 7.7로 상대적으로 높은 오차값이 나타나며, TPOT은 MAPE 32.2%, MAD 3.3의 작은 오차값을 나타내고 있다. 금회 연구에서 4개 프로젝트에 적용한 TPOT가 2개 프로젝트에 적용한 LightGBM 라이브러리 보다 오차값이 적은 것으로 분석되었다.
토질별 예측 결과분석
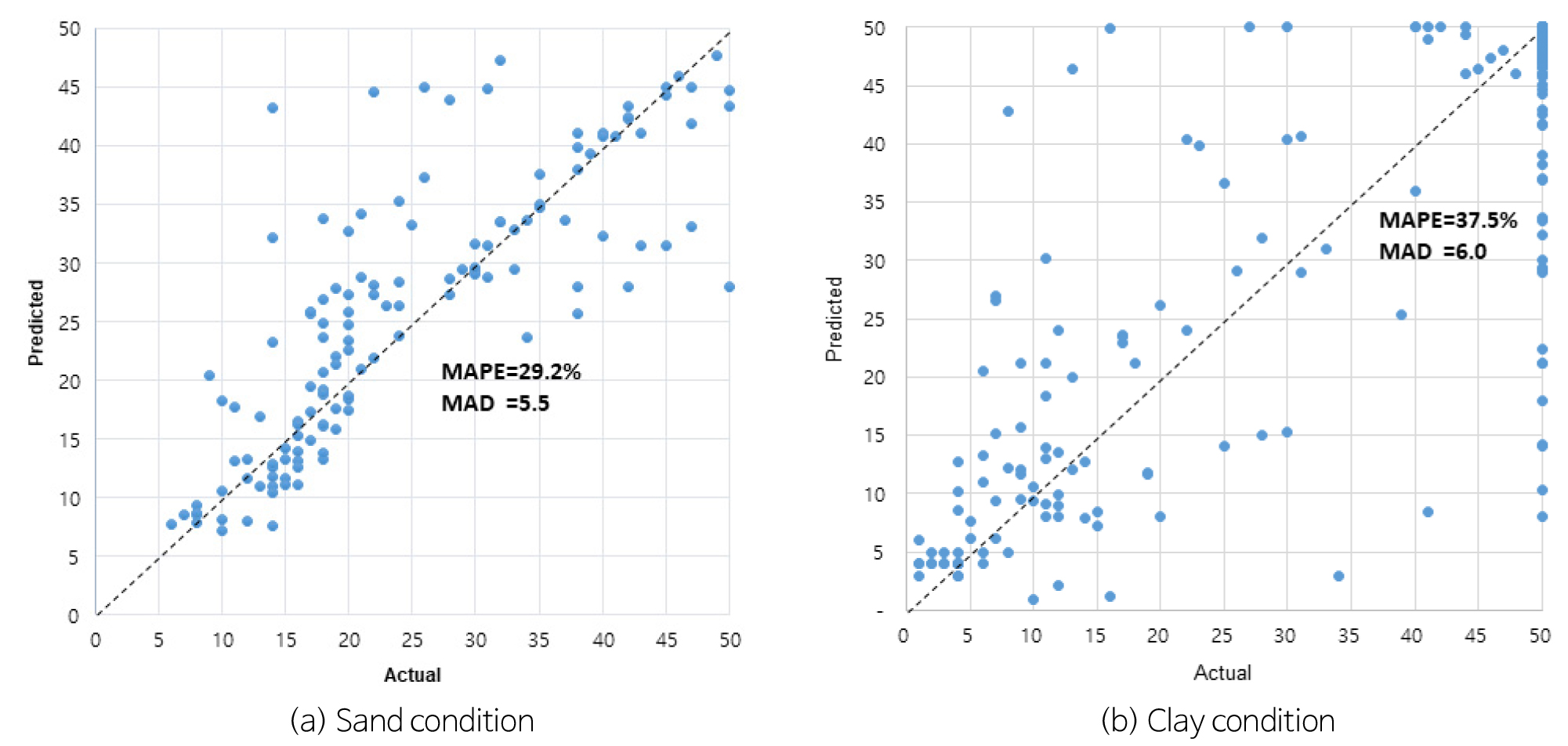
AI 예측은 토질 조건별로 검토해 보았다. 토질 조건은 조립토를 모래로 세립토를 점토로 구분하였으며, 2개 프로젝트(E, IN)는 모래지반, 4개 프로젝트(IA, IP, M, R)는 점토지반으로 분류되었다. 각각 예측값과 실측값의 결과는 Fig. 13과 같다. 모래지반의 경우 예측값은 MAPE 29.2%, MAD 5.0, 점토지반의 경우는 MAPE 37.5%, MAD 6.0로 분석되었다. 토질 조건별 연구에서 모래지반에 대한 예측 성능이 상대적으로 양호한 것으로 분석되었다.
모래지반은 대체로 실측값보다 예측값이 크게 나타나는 경향을 보이고 있어서 적용 시 보정값을 이용한 예측값 축소가 필요하며, 점토지반은 N치가 50인 단단한 지지층에서 일부 예측이 적게 나타나고 있어서 설계 적용 시 오류를 가져올 수 있다. 점토지반 예측에 대한 불확실성이 보다 커서 이에 대한 보정값 및 추가 모델에 대한 연구를 계속적으로 수행해야 할 것이다. 점토지반은 지표부근의 연약층과 단단한 지지층 사이의 값이 과다하여 이중층으로 분리 후 AI를 학습하는 방안을 고려하여야 한다.
예측N치 3차원 분포
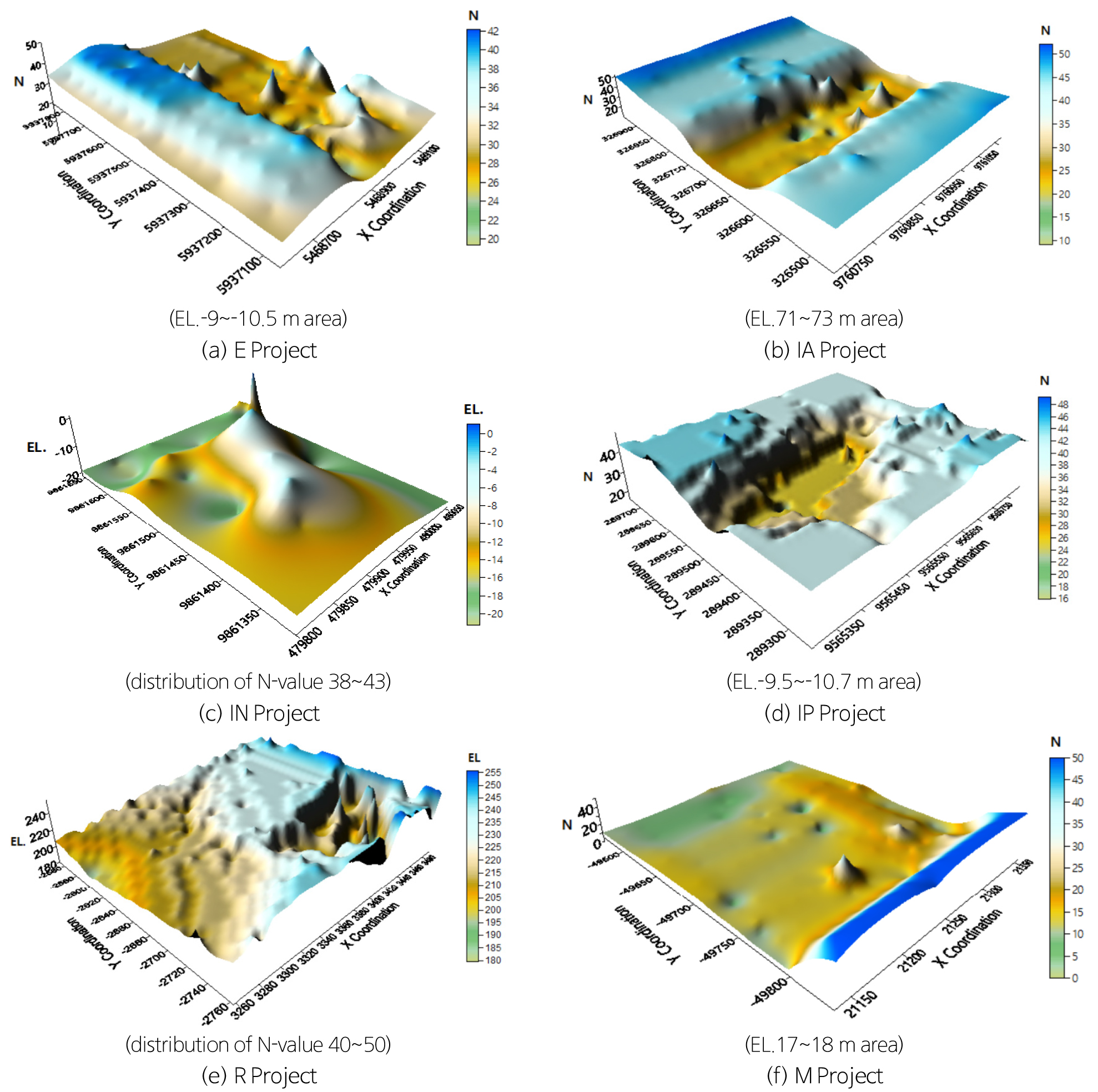
AI 예측은 6개 프로젝트에서 수행 후, 각각 학습값인 학습 데이터의 N치와 임의 점에서 예측된 N치를 통합하여 3차원으로 표현하였다. 임의 점에서 예측된 N치는 최대값과 최소값으로 정규화된 X좌표 12건, Y좌표 12건 그리고 심도 24건을 각각 고려하여 위치별로 예측되었다. 이들 값은 Surfer 프로그램 내 kriging 기법을 이용하여 3차원으로 분포도를 작성하였다(Fig. 14).
E 프로젝트는 EL.-9~-10.5 m 구간에서 동측(N치 25~35)에 비해 서측(N치 40 이상)이 비교적 더욱 양호한 지지층이 분포되는 것을 파악 할 수 있다. 서측은 말뚝 선단지지력의 확보가 가능하나 동측은 주면마찰력을 이용하며 선단 지지층은 더욱 하부에 분포하는 것을 알 수 있었다. IA 프로젝트는 EL.71~73 m 구간에서 중간부(N치 20~30)가 남북측(N치 40 이상) 보다 적은 N치 분포를 나타내고 있다. IN 프로젝트는 N치 분포가 양호한 지반분포를 보기 위한 것으로 N치 38~43은 중간부 구간의 EL.-2~-8 m에서 존재하며, 외측으로 갈수록 상대적으로 심도가 깊은 곳에서 양호한 지반이 분포하는 것으로 분석되었다. 그 외 3차원 N치 분포는 조건별 고려 후 추가로 확인 할 수 있다. IP 프로젝트는 EL.-9.5~-10.7 m 구간에서 지반의 분포가 불규칙한 경향을 보이며, N치 30정도가 중간부에 분포하고 그 외부 쪽으로 N치가 분포하는 것으로 분석되었다. 중간부의 말뚝 선단지지층은 심도별 3차원 분포도를 작성 후 적정한 위치를 파악할 수 있다.
R 프로젝트는 N치 분포가 양호한 지반분포를 보기 위한 것으로 N치 40 이상 분포구간은 동북측 구간의 EL.255~230 m에서 분포하며, 동남측과 서측에서는 EL.225 m 이하 보다 깊은 곳에서 분포하는 것으로 분석되었다. 이곳은 학습 시추자료가 7공으로 부족하여 예측값의 신뢰도가 약간 떨어지고 있다. 이러한 곳은 AI 예측값의 오류가 존재하므로 가급적 추가적인 시추조사를 통해 학습 자료 확보가 필요한 여건이다. 또한 부족한 시추공의 학습 자료를 통해 예측 할 수 있는 라이브러리의 추가 연구개발이 필요하다.
M 프로젝트는 EL.17~18 m 구간에서 일부 남측(N치 45 이상)에 지지층이 분포하며, 그 외 구간에서는 N치 30 이하로 분포하는 경향으로 분석되었다. 이곳은 대체로 지층분포가 실측값과 예측값이 유사하게 나타나고 있다.
위와 같이 예측 N치를 적용하여 입찰 시 구조물 구간의 지반개량이나 기초 설계를 수행할 경우, 제한적인 해외사업 입찰 기간 내에 효율적이고 신뢰성 높은 최적 설계와 물량산출을 수행 할 수 있을 것으로 판단된다. 현재까지 연구개발은 프로젝트별 적용 및 검증을 통해 최적의 AI 모델을 선정할 수 있으며 실용화 가능성을 고려할 수 있었다.
결론 및 고찰
본 연구에서는 폴란드, 인도네시아, 말레이시아에서 수행한 6개 프로젝트 현장자료를 근거로 AI를 적용하여 미시추 지점에서 N치를 예측하였다. 예측N치와 실제 시추공에서 구한 실측N치와 비교하여 타당성 여부를 검토하였으며, 연구 결과는 다음과 같다.
(1) AI는 학습 성능을 높이기 위해 ‘원형증강법’을 이용하여 빅 데이터화 하였으며, 실측N치 1개 당 추가로 36개를 생성시키고, 학습값을 0.0~1.0 사이로 정규화 하는 전처리 작업을 실시하였다.
(2) AI 기법은 인공신경망, 의사결정나무, 오토 머신러닝을 적용하여 신뢰성 분석 후 최적의 모델을 적용하였으며, 학습에 적용된 입력인자인 각 프로젝트의 위도, 경도, Elevation, 심도, 토질종류를 가지고 심도별 표준관입시험 자료를 학습한 후 N치를 예측하는 개발을 실시하였다.
(3) 선정된 모델 중 의사결정나무는 IA, M 프로젝트에 적용되었으며, 오토 머신러닝은 E, IN, IP, R 프로젝트에 적용되었다. 금회 연구에서 인공신경망은 상대적으로 신뢰성이 낮아 적합하지 않은 것으로 분석되었다.
(4) 표준관입시험에서 구한 실측N치와 AI가 예측한 N치를 검토해 본 결과, MAPE는 E 프로젝트에서 20.3%, IA 프로젝트 47.4%, IN 프로젝트 37.8%, IP 프로젝트 31.9%, R 프로젝트 37.0%, M 프로젝트 35.8%로 각각 분석 되었다. N치 예측에 적용된 평균절대백분율오차(MAPE)는 상대적인 증감을 표현하기 때문에 한계성이 파악되었으며, 추후 연구 시 신뢰성 분석은 평균절대편차(MAD)를 적용해야 함을 알 수 있었다.
(5) AI는 대체적으로 실측값과 유사한 경향으로 N치를 예측하고 있으며, 지표인근의 점토 및 모래에서는 실측값과 오차를 가지고 예측되었다. 하지만 N치 40 이상의 말뚝 지지층은 실측값과 유사한 경향으로 예측되었다(Figs. 6, 7, 8, 9, 10, 11). 추후 건기 ‧ 우기 지하수위 변동에 따른 영향을 고려한 연구가 추가 요구되고 있다.
(6) 모델별 예측시, 2개 프로젝트에 적용한 LightGBM 예측값은 MAPE 41.8%, MAD 7.7로 나타나며, 4개 프로젝트에 적용된 TPOT은 MAPE 32.2%, MAD 3.3으로 오차값이 적은 것으로 분석되었다. 또한 토질 조건별 예측 결과, 모래지반 2개 프로젝트는 MAPE 29.2%, MAD 5.0, 점토지반 4개 프로젝트는 MAPE 37.5%, MAD 6.0로 모래지반에 대한 예측값이 양호한 것으로 분석되었다.
(7) 임의 점에서 예측된 N치 X좌표 12건, Y좌표 12건 그리고 심도 24건과 실측값까지 고려하여 3차원 N치 분포를 표현하였다. 이 연구로 심도별 지반분포와 지반특성을 3차원으로 쉽게 파악 할 수 있었다. 금회 연구에서 적용된 토질 조건은 해외 프로젝트 6건 이였으며, 추후 국내 토질 조건별 특성을 고려한 N치 예측방법을 연구 할 것이다.
(8) 지표인근과 저심도에서 예측값은 실측값과 다소 오차가 발생되고 추가 연구 시 지표인근의 연약층과 고심도의 단단한 지지층을 이중층으로 분리하여 각각 AI를 학습시키는 보정 방안이 검토되어야 한다.